Питання до державного екзамену з дисципліни “Теоретична механіка”

1. Сила, її момент відносно точки та осі (сила, її характеристики, проекція сили на вісь і на площину, аналітичний спосіб задавання сили; момент сили відносно точки, осі).

2. Система збіжних сил, момент рівнодійної системи збіжних сил (основні поняття, приведення системи збіжних сил до рівнодійної, умови рівноваги просторової та площинної системи збіжних сил).

3. Основні рухи абсолютно твердого тіла (завдання руху твердого тіла, поступальний рух, обертальний рух навколо нерухомої осі, швидкість і прискорення точок тіла, що обертається навколо нерухомої осі).

4. Плоскопаралельний рух твердого тіла (кінематичні рівняння руху, швидкість точок тіла при плоскопаралельному русі, план швидкостей, миттєвий центр швидкостей, поняття про центроїди, прискорення точок тіла при плоскопаралельному русі).

5. Складний рух точки (основні поняття, абсолютна та відносна похідні від вектора, теорема про складання швидкостей, теорема про складання прискорень – теорема Коріоліса, правило Жуковського).

6. Диференціальне рівняння руху матеріальної точки. Основні задачі динаміки (диференціальне рівняння руху вільної матеріальної точки, перша основна задача динаміки, друга основна задача динаміки, умови прямолінійного руху матеріальної точки).

Методичні рекомендації щодо підготовки до державного екзамену з дисципліни “Теоретична механіка”

для студентів очної форми навчання

спеціальності 6.010103 “Педагогіка і методика середньої освіти.

Трудове навчання”

освітньо-кваліфікаційний рівень – бакалавр

Плоскопаралельний рух твердого тіла (кінематичні рівняння руху, швидкість точок тіла при плоскопаралельному русі, план швидкостей, миттєвий центр швидкостей, поняття про центроїди, прискорення точок тіла при плоскопаралельному русі).

Кінематичні рівняння руху

Плоскопаралельним рухом твердого тіла називається такий рух, при якому плоска фігура, утворена внаслідок перерізу тіла деякою нерухомою площиною, залишається у цій площині.

При плоскому русі кожна точка тіла описує плоску траєкторію, розміщену в площині, паралельній цій нерухомій площині. Прикладом тіла, що здійснює плоскопаралельний рух, є циліндр, який котиться по горизонтальній площині. Всі точки циліндра переміщуються в площинах, паралельних площині .
Розглянемо довільний плоскопаралельний рух твердого тіла. Нехай всі точки тіла переміщуються в площинах, паралельних нерухомій площині . Пересічемо тіло площиною . З визначення плоскопаралельного руху і властивостей твердого тіла випливає, що будь-яка пряма , проведена в тілі перпендикулярно площині , буде переміщуватися поступально,

тобто траєкторії, швидкості та прискорення всіх точок цієї прямої будуть однаковими. Таким чином, для визначення руху тіла необхідно знати рух лише однієї точки на кожній прямій, проведеній перпендикулярно площині . Якщо взяти точки в одній площині, паралельній площині , можна стверджувати, що плоскопаралельний рух тіла визначається рухом плоскої фігури, одержаної від перерізу тіла будь-якою площиною, паралельною площині . У свою чергу, положення плоскої фігури у своїй площині повністю визначається положенням двох будь-яких її точок, наприклад, і , тобто відрізком .

Плоскопаралельний рух плоскої фігури можна здійснити двома простими рухами:

1. поступальним, що передбачає переміщення тіла з положення у положення ;

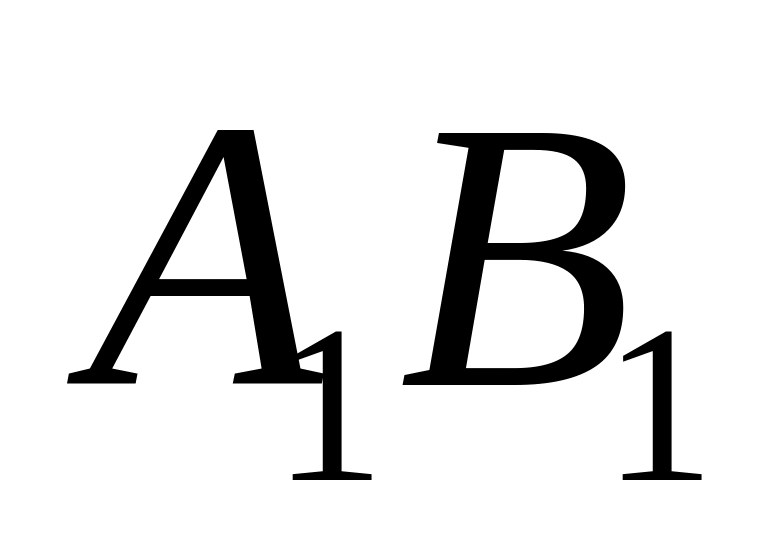2. обертальним, що полягає в обертанні тіла з положення 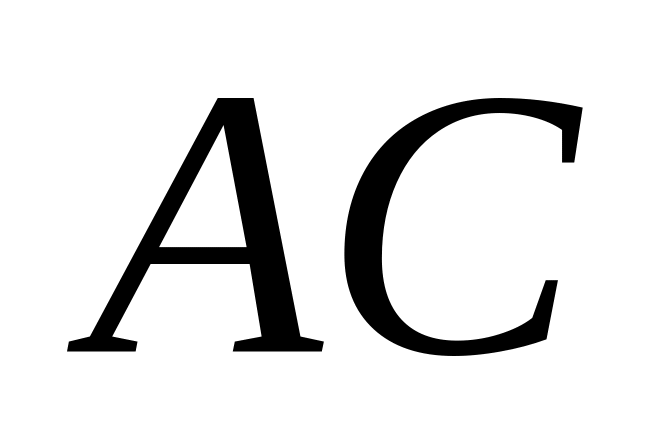у положення .

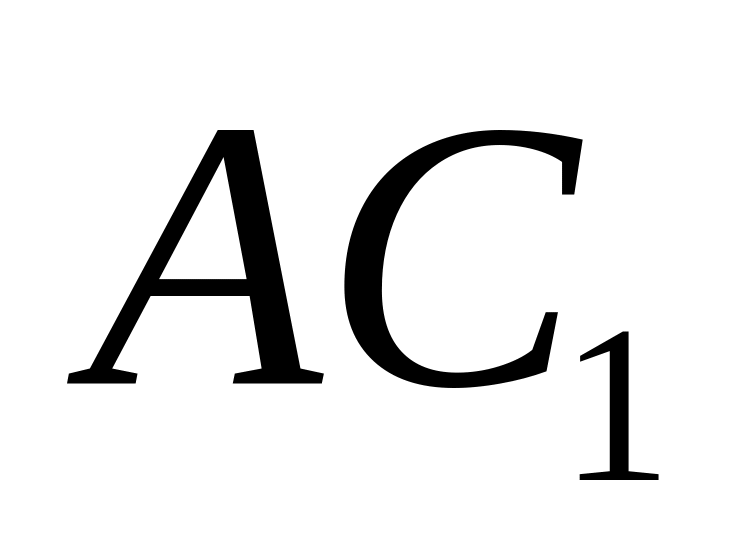Точка, навколо якої фігура здійснює обертання, називається полюсом (т. А).

Рух плоскої фігури визначається трьома незалежними параметрами: координатами т. і кутом повороту плоскої фігури навколо т. А:

– кінематичні рівняння твердого тіла, що здійснює плоскопаралельний рух.

Швидкість при плоскопаралельному русі

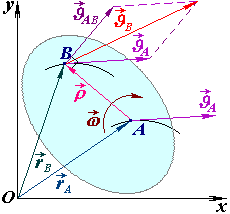
Залежність між швидкостями точок плоскої фігури визначається за теоремою: швидкість будь-якої точки плоскої фігури дорівнює геометричній сумі швидкості полюса і швидкості цієї точки при обертанні плоскої фігури навколо полюса.

приймемо за полюс ( ). Вектор перпендикулярний до площини рисунка, направлений від нас. Визначимо швидкість будь-якої іншої точки плоскої фігури, наприклад . Для цього проведемо з нерухомої (початку нерухомої системи координат, відносно якої рухається плоска фігура) в і радіус-вектори і . Радіус-вектор можна задати за допомогою двох векторів (1)

Ця залежність буде зберігатися протягом усього часу руху.

Оскільки радіус-вектор з’єднує дві точки ( і ) плоскої фігури, то за весь час руху він обертається навколо полюса з кутовою швидкістю плоскої фігури , не змінюючись за модулем, тобто .

Продиференціюємо обидві частини рівності за часом:

(2)

Похідні від векторів і за часом – це швидкості відповідно і .

Оскільки під час руху плоскої фігури модуль радіус-вектора залишається незмінним, а його напрям при повороті фігури змінюється, то похідна – це обертова швидкість навколо полюса : .

Обертова швидкість точки твердого тіла дорівнює: . Тоді,

,

де – кутова швидкість обертання фігури навколо полюса . Тоді формула (2) матиме вигляд:

(3)

Теорему доведено.

Обертова швидкість направлена перпендикулярно до відрізка в сторону обертання фігури. Її модуль дорівнює:

Швидкість зображується діагоналлю паралелограма, побудованого з на швидкості полюса , перенесеної в , і обертовій швидкості навколо полюса .

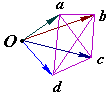
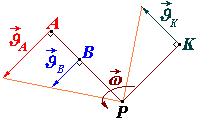
План швидкостей

Залежність між швидкостями точок плоскої фігури дає змогу визначити швидкості точок цієї фігури шляхом наочної побудови, що називається планом швидкостей.

Припустимо, що відомі швидкості точок плоскої фігури. Відкладемо з довільної за напрямом швидкостей даних точок відрізки , що дорівнюють швидкостям цих точок ( і т.д.). З’єднаємо відрізками.

Виконана побудова називається планом швидкостей; відрізки – променями; – вершинами плану швидкостей.

З :

З :

З :

і т. д.

Відповідно, кожний відрізок, що з’єднує вершини плану швидкостей, геометрично рівний обертовій швидкості відповідної точки фігури навколо іншої точки як навколо полюса.

Тому, 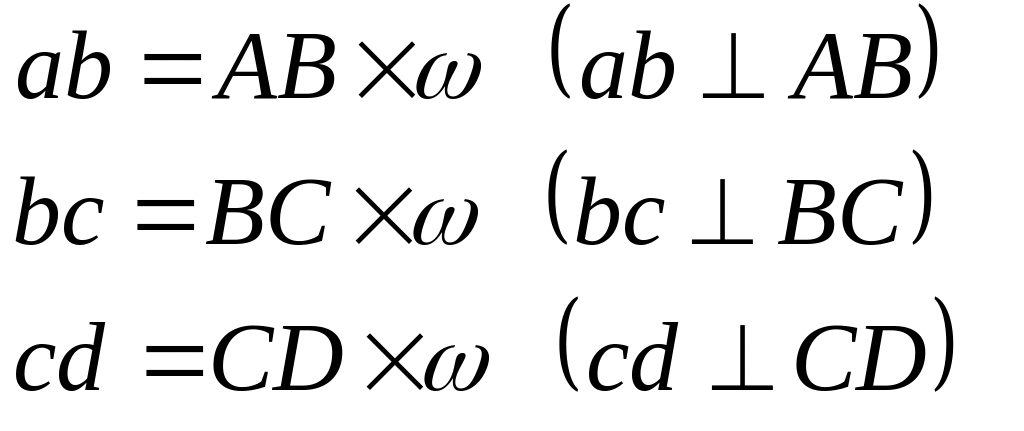і т.д.

Звідси слідує, що багатокутник подібний до багатокутника і повернутий відносно нього на кут в сторону обертання плоскої фігури.

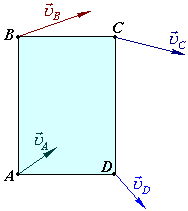
Для побудови плана швидкостей точок плоскої фігури необхідно знати:

• модуль і напрям швидкості однієї точки цієї фігури;

• пряму, по якій напрямлена швидкість будь-якої іншої точки фігури.

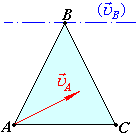
Припустимо, що відомі:

• модуль і напрям швидкості трикутної пластини , що рухається у площині креслення;

• пряма, по якій напрямлена швидкість цієї пластини.

Необхідно знайти і шляхом побудови плану швидкостей.

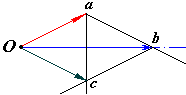
1. Проведемо з довільної відрізок і пряму, паралельну .

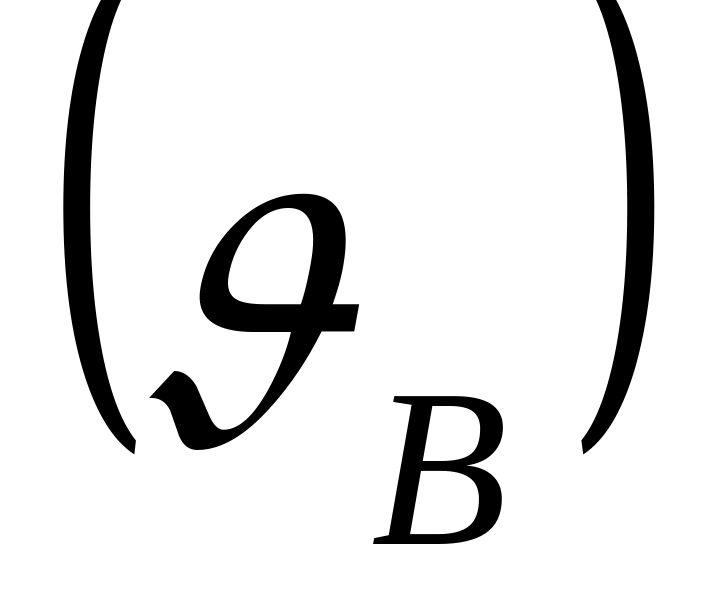2. Відомо, що відрізки, які з’єднують вершини плану швидкостей, перпендикулярні до відрізків, які з’єднують відповідні точки фігури.

3. Щоб визначити вершину плану швидкостей, проведемо з вершини пряму перпендикулярну до . Точка перетину її з прямою, по якій напрямлена швидкість , є вершиною , а відрізок .

4. Щоб визначити вершину плану швидкостей, проведемо з вершин і прямі перпендикулярні відповідно до і трикутника. Перетин цих прямих утворить вершину . Відрізок .

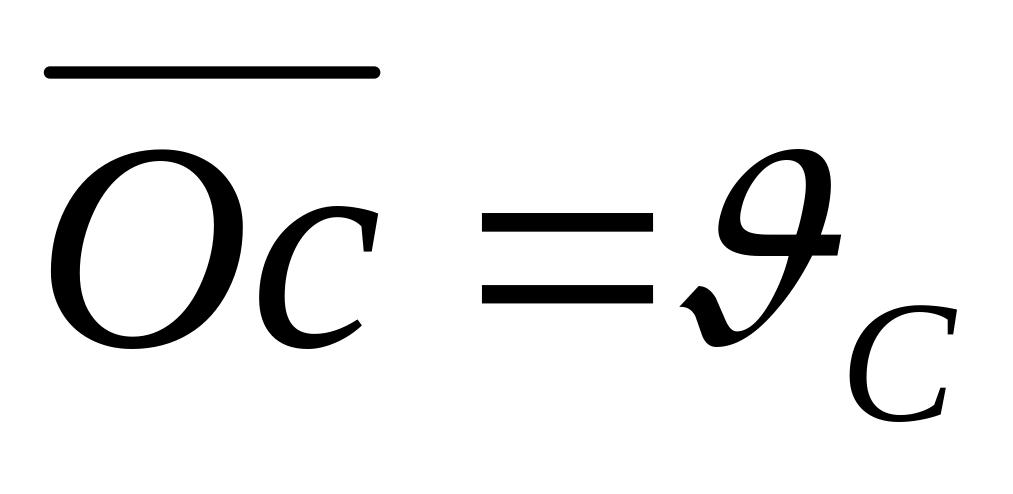Аналогічною побудовою можна визначити швидкість будь-якої точки плоскої фігури, з’єднавши її з двома точками, швидкості яких уже відомі.

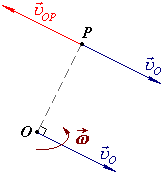
Миттєвий центр швидкостей

Миттєвий центр швидкостей – точка плоскої фігури, швидкість якої в даний момент часу дорівнює нулю.

Припустимо, що відомі швидкість довільної плоскої фігури і кутова швидкість фігури в деякий момент часу. Вважатимемо, що – полюс. Тоді швидкість будь-якої точки фігури буде дорівнювати геометричній сумі швидкості полюса і обертовій швидкості точки навколо цього полюса. Проведемо з перпендикуляр до напряму швидкості , так щоб напрям повороту швидкості

відповідно до цього перпендикуляру співпав з напрямом обертання фігури.

Обертові швидкості всіх точок цього перпендикуляру навколо полюса протилежно напрямлені до швидкості полюса.

Знайдемо таку , обертова швидкість якої дорівнює за модулем швидкості полюса , тобто . Оскільки напрями цих швидкостей протилежні, то .

Швидкість :

Відповідно, в даний момент часу є миттєвим центром швидкостей.

Визначимо положення . Модуль обертової швидкості навколо полюса :

Тобто, миттєвий центр швидкостей плоскої фігури знаходиться на перпендикулярі до напряму швидкості полюса на відстані від полюса, що дорівнює .

Визначимо швидкості плоскої фігури, прийнявши за полюс миттєвий центр швидкостей .

За формулою (8.3): (в даний момент) , тобто

швидкість будь-якої точки плоскої фігури в даний момент часу становить обертову швидкість цієї точки навколо миттєвого центру швидкостей.

Тому, 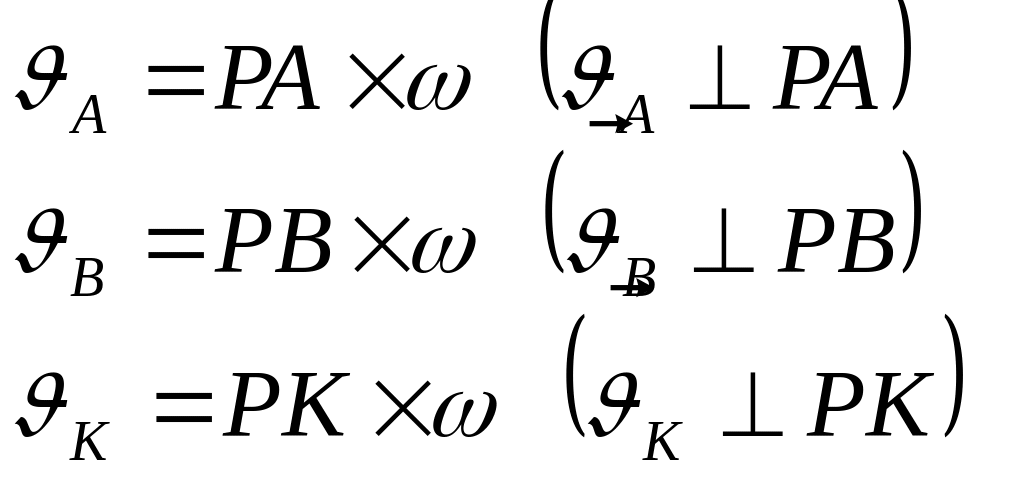, тобто

швидкість будь-якої точки плоскої фігури в кожний момент часу має модуль, що дорівнює добутку кутової швидкості фігури на довжину відрізка, який з’єднує точку з миттєвим центром швидкостей, і напрямлена перпендикулярно до цього відрізка в сторону обертання фігури.

Знайдемо залежність між швидкостями точок плоскої фігури в даний момент часу:

і т.д., тобто

модулі швидкостей точок плоскої фігури в кожний момент часу пропорційні відстаням від цих точок до миттєвого центру швидкостей.

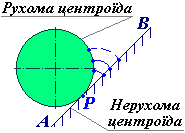
Поняття про центроїди

При русі плоскої фігури в її площині миттєвий центр швидкостей переміщується від однієї точки фігури до іншої, займаючи кожного разу нові положення.

Геометричне місце миттєвих центрів швидкостей (траєкторія), відмічених на площині, що жорстко зв’язана з плоскою фігурою, називається рухомою центроїдою.

Геометричне місце миттєвих центрів швидкостей (траєкторія), відмічених на нерухомій площині, називається нерухомою центроїдою.

Розглянемо кочення без ковзання колеса по нерухомій площині. У цьому випадку нерухомою центроїдою є пряма АВ, рухомою – коло колеса. У кожний момент часу рухома і нерухома центроїди мають спільну точку – миттєвий центр швидкості Р, тобто точку, швидкість якої дорівнює нулю. Тому плоский рух можна представити як кочення без ковзання рухомої центроїди по нерухомій.

Прискорення при плоскопаралельному русі

Прискорення точок плоскої фігури визначається теоремою: прискорення будь-якої точки плоскої фігури дорівнює геометричній сумі прискорення полюса і прискорення даної точки при рухові разом з плоскою фігурою навколо полюса.

Припустимо, що відомі прискорення деякої точки плоскої фігури і алгебраїчні величини кутової швидкості і кутового прискорення плоскої фігури і . Прискорення будь-якої фігури за умови, що – полюс:

Прискорення знайдемо як векторну похідну за часом від швидкості цієї точки:

Оскільки ; , маємо .

– обертове прискорення у процесі руху навколо полюса ;

– центробіжне прискорення у процесі руху навколо полюса .

Тому

Але геометрична сума обертового і центробіжного прискорень і є повним прискоренням у процесі руху разом з плоскою фігурою навколо полюса :

Звідси: .

Сила, її момент відносно точки та осі (сила, її характеристики, проекція сили на вісь і на площину, аналітичний спосіб задавання сили; момент сили відносно точки, осі).

Сила та її характеристики

Сила – векторна величина, що є мірою механічної взаємодії матеріальних тіл.

Сила характеризується:

1. Числовим значенням (модулем). Модуль сили знаходять шляхом її порівняння із силою, прийнятою за одиницю. Одиниця виміру сили у Міжнародній системі одиниць (СІ) – 1 ньютон 1 Н – це сила, яка надає тілу масою 1 кг прискорення 1 м/с² у напрямі дії сили. 9,81 Н  1 кг.

2. Напрямом. Напрям сили – напрям руху, який дістало б тіло, що перебуває у спокої, якби на нього подіяла ця сила.

3. Точкою прикладання. Точкою прикладання сили називається матеріальна частина, на яку діє сила.

т. А – точка прикладання (початок вектора); т. В – кінець вектора; тп – лінія дії сили – пряма, вздовж якої напрямлена сила.

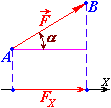
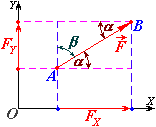
Проекція сили на вісь

Проекція вектора сили на вісь – це алгебраїчна (скалярна) величина, що дорівнює добутку модуля сили на косинус кута між силою і додатнім напрямом осі.

	Проекцію вважають додатною, якщо напрями проекції та осі збігаються, або якщо кут між напрямом вектора сили і віссю (кут ) – гострий.
	Проекцію вважають від’ємною, якщо напрям проекції протилежний напряму осі, або якщо кут між напрямом вектора сили і віссю (кут ) – тупий.
	Проекція сили на вісь перетворюється на нуль, якщо ця сила перпендикулярна до цієї осі, або якщо кут між напрямом вектора сили і віссю (кут ) – прямий.

Проекція вектора сили на дві взаємно перпендикулярні осі

Якщо вектор сили на одну з осей координат проектується через косинус кута , то на іншу перпендикулярну вісь його проекція виражається через синус кута .

Аналітичний спосіб задавання сили

Модуль сили визначають з за теоремою Піфагора: . Кути, що визначають напрям вектора сили на площині: .

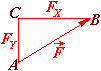
Проекція сили на площину

Проекція вектора сили на площину – вектор, що знаходиться між проекціями початку і кінця сили на цю площину.

Модуль проекції вектора на площину :

Якщо кут між вектором сили і віссю невідомий, то вектор спочатку проектують на площину, в якій розміщена вісь, а потім – на вісь.

– вектор сили; – проекція вектора сили на площину , в якій розміщена вісь ; – проекція вектора сили на вісь ; – кут між вектором сили і площиною ; – кут між проекцією вектора сили на площину і віссю .

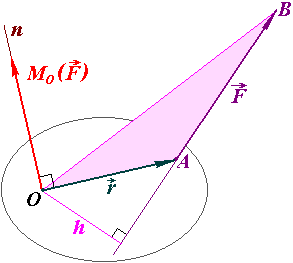
Момент сили відносно точки (центра)

Т. О, відносно якої береться момент, називається центром моменту.

Момент сили відносно точки О – момент відносно центра.

Перпендикуляр, опущений з т. О, відносно якої розглядають момент сили, на лінію дії сили, називається плечем сили . Момент сили відносно центра О визначається: модулем моменту; положенням у просторі площини ОАВ (площини повороту), що проходить через центр О і силу ; напрямом повороту в цій площині.

Моментом сили відносно точки О (центру) називається прикладений в точці О вектор , модуль якого дорівнює добутку значення сили на її плече . Вектор напрямлений перпендикулярно до площини, що проходить через центр О і силу, в ту сторону, звідки “обертання” тіла під дією сили відносно точки О було б видно проти руху годинникової стрілки.