2.2. Математическая постановка (модель) задачи скалярной оптимизации

Решение считается оптимальным, если оно удовлетворяет множеству ограничений (выделяющих область допустимых решений (ОДР))

Решение считается оптимальным, если оно удовлетворяет множеству решений и обеспечивает множество значений заданного критерия оптимальности.

Критерий оптимальности (показатель качества, целевая функция, функция предпочтения, функция полезности, функция потерь и др.) есть функция или функционал (функция от функции), наибольшее или наименьшее значение которого указывает на оптимум.

Q Q → max Q

A

х_opt

х

ОДР

Критерии оптимальности могут быть технические (кпд, масса, удельный расход сырья и тд), экономические (прибыль, рентабельность, затраты), экологические, критерии безопасности.

Данной математической схеме соответствуют различные математические варианты, практические задачи, которые рассматриваются и решаются теорией скалярной (однокритериальной) оптимизации.

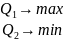
В обобщенном статическом варианте задачу скалярной оптимизации можно записать следующим образом:

Q = Q (A, E, X) → extr

при выполнении условий:

F _j (X, E, C) B_j; j=1,m;

где х = {x₁, x₂, x₃, ... x_n}, x_j < Ω_x;

E = {l₁, l₂, l₃, ... l_n};

A = {a₁, a₂, a₃, ... a_n} – вектор коэффициентов персонала;

B = {b₁, b₂, b₃, ... b_n} – вектор коэффициентов неравенств;

C = {с₁, с₂, с₃, ... с_n} – вектор функций Fj от точки;

Ω_x – область допустимых значений вектора_.

В динамическом варианте задачу скалярной оптимизации можно представить на примере управления динамическим объектом.

S(∙)

О. У.

U(t) Y(t)

Определить непрерывность вектор-функцию U(t), Y(t), что обеспечивают минимум критерия при выполнении ограничений:

– ограничение I рода;

- ограничения II рода;

Ω – заданные области значений переменных.

y

Ω_ywT

Ω_y0

t

y

Ω_uwT

Ω₀

Ω _{u 0} t

t_o t₀+T

F (Y, U, t) – функция, учитывающая, например, расход топлива на управление.

Q max=super

max

int min

ОДР

х

В зависимости от наличия или отсутствия задачи факторов неопределенности Е она относится к одному из следующих 3 видов:

а) задача оптимизации в условиях определенности – вектор Е=Ø;

б) задачи оптимизации в условиях риска. При этом считается, что известен закон распределения вероятностей для вектора Е или для функции некоторого вектора;

в) задачи оптимизации в условиях неопределенности. Здесь предполагается, что известен интервал возможных значений вектора Е.

В зависимости от характера критерия оптимальности, ограничений Q(∙), I(∙). В зависимости от характера искомых переменных Х, Y различают следующие множества задач скалярной оптимизации:

• задачи линейного программирования

• задачи нелинейного программирования

• задачи динамического программирования

• задачи целочисленного программирования

• задачи стохастического программирования

• и др.

Рассмотрим достоинства и недостатки задач скалярной оптимизации.

К числу достоинств оптимизации относятся:

• относительная простота;

• наличие разработанных и испытанных методик;

• наличие прикладных пакетов программ.

К недостаткам данной математической схемы оптимизации относятся:

• чувствительность к нарушению предпосылок (условий правильного применения);

• данная схема не работает при наличии многих критериев оптимизации;

• данная схема не охватывает слабо характеризованные задачи, требующие участия человека.