Умножив обе части уравнения слева на матрицу , получим

(2.6.3)

Оценки, полученные с помощью МНК, являются случайными величинами, так как представляют собой линейную комбинацию случайных величин у₁, у₂, … у_n.

При выполнении предпосылок множественного регрессионного анализа оценка метода наименьших квадратов является эффективной, то есть обладает наименьшей дисперсией в классе линейных несмещенных оценок.

Преобразуем вектор оценок (2.6.3) с учетом (2.6.2)

_или

= , (2.6.4)

то есть оценки параметров (2.6.3), найденные по выборке, будут содержать случайные ошибки.

Покажем, что математическое ожидание оценки равно оцениваемому параметру :

,

так как . Таким образом, очевидно, что вектор есть несмещенная оценка вектора параметров .

Вариации оценок параметров будут в конечном счете определять точность уравнения множественной регрессии. Для их измерения в многомерном регрессионном анализе рассматривают так называемую ковариационную матрицу оценок параметров :

=

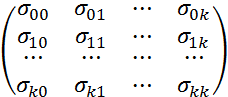
где - ковариации оценок параметров и . Ковариация двух переменных определяется как математическое ожидание произведения отклонений этих переменных от их математических ожиданий. Поэтому

(2.6.5)

Ковариация характеризует как степень рассеяния значений двух переменных относительно их математических ожиданий, так и взаимосвязь этих переменных.

В силу того, что оценки , полученные методом наименьших квадратов, являются несмещенными оценками параметров , т. е. , выражение (2.6.5) примет вид:

.

Рассматривая ковариационную матрицу , легко заметить, что на ее главной диагонали находятся дисперсии оценок параметров регрессии, так как

. (2.6.6)

В матричном виде ковариационная матрица вектора оценок параметров имеет вид:

( в этом легко убедиться, перемножив векторы и ).

Учитывая (2.6.4), преобразуем это выражение:

(2.6.7)

ибо элементы матрицы Х – неслучайные величины.

Матрица представляет собой ковариационную матрицу вектора возмущений

,

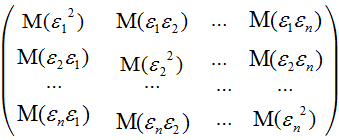в которой все элементы, не лежащие на главной диагонали, равны нулю в силу предпосылки о некоррелированности возмущений и между собой, а все элементы, лежащие на главной диагонали, в силу предпосылок регрессионного анализа равны одной и той же дисперсии :

.

Поэтому матрица

,

где - единичная матрица n-го порядка. Следовательно, в силу (2.6.7) ковариационная матрица вектора оценок параметров:

или (2.6.8)

Итак, с помощью обратной матрицы определяется не только сам вектор оценок параметров, но и дисперсии и ковариации его компонент.

Прогноз по модели множественной линейной регрессии для вектора переменных составит

(2.6.9)

Дисперсия ошибки прогноза определяется по формуле

. (2.6.10)

В качестве оценки используется

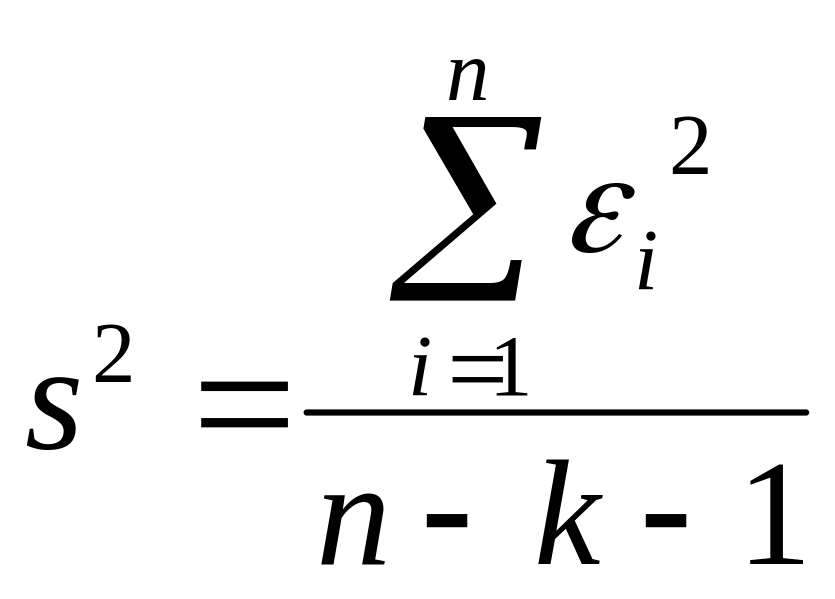. (2.6.11)

Тогда оценка дисперсии ошибки прогноза

_{(2.6.10 а)}

Качество всей модели в целом определяется по критерию Фишера

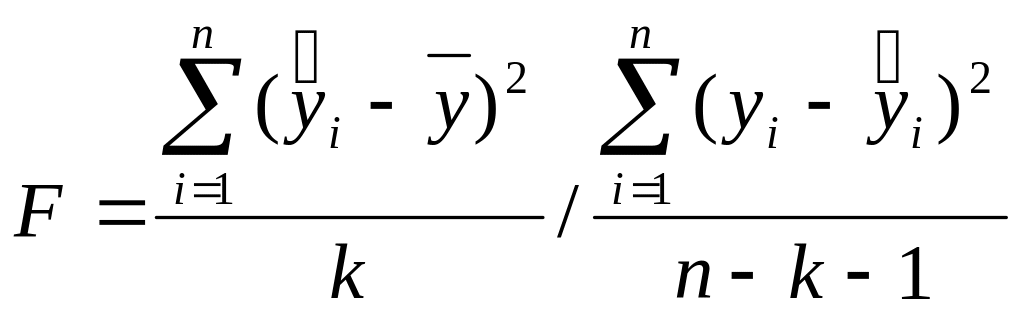. (2.6.12)

Если , то уравнение регрессии в целом незначимо.

Здесь - табличное значение критерия Фишера с k и n-k-1 степенями свободы уровня значимости .

Может быть рассчитан коэффициент детерминации, отражающий долю объясненной факторами дисперсии в общей дисперсии

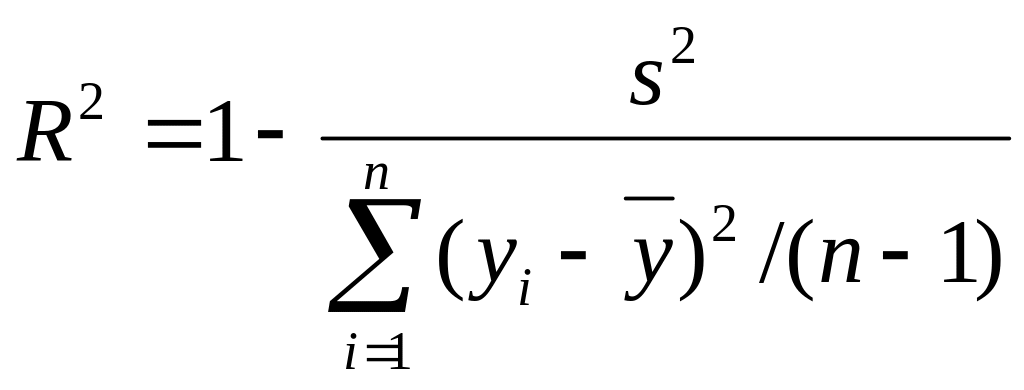. (2.6.13)

Правило проверки статистической значимости оценок (i=0,…,k) основывается на проверке статистической гипотезы

Н₀: .

Для этого вычисляется статистика

, (2.6.14)

которая при выполнении гипотезы Н₀ распределена по закону Стьюдента с n-k-1 степенями свободы.

Если , гипотезу Н₀ следует отклонить и признать коэффициент статистически значимым. В противном случае следует признать статистически незначимым и переменную X_i исключить из регрессионной модели.

6. НЕКОТОРЫЕ ВОПРОСЫ ПРАКТИЧЕСКОГО ПРИМЕНЕНИЯ

РЕГРЕССИОННЫХ МОДЕЛЕЙ

Ранее нами была изучена классическая линейная модель множественной регрессии. Однако мы не касались некоторых проблем, связанных с практическим использованием модели множественной регрессии. К их числу относится мультиколлинеарность.

Под мультиколлинеарностью понимается высокая взаимная коррелированность объясняющих переменных. Мультиколлинеарность может проявляться в функциональной и стохастической формах.

При функциональной форме мультиколлинеарности по крайней мере одна из парных связей между объясняющими переменными является линейной функциональной зависимостью. В этом случае матрица Х^TX особенная, так как содержит линейно зависимые векторы-столбцы и ее определитель равен нулю. Это приводит к невозможности решения соответствующей системы уравнений и получения оценок параметров регрессионной модели.

Однако в экономических исследованиях мультиколлинеарность чаще всего проявляется в стохастической форме, когда между хотя бы двумя объясняющими переменными существует тесная корреляционная связь. Матрица Х^TX в этом случае является неособенной, но ее определитель очень мал. В результате получаются значительные дисперсии оценок коэффициентов регрессии

Наличие мультиколлинеарности системы объясняющих переменных можно статистически проверить по тесту Глобера – Феррара.

При отсутствии мультиколлинеарности статистика

, (2.7.1)

где – объем выборки;

- количество объясняющих переменных;

det – определитель выборочной корреляционной матрицы объясняющих переменных ,

имеет - распределение с k(k-1)/2 степенями свободы.

Вычисленное значение сравнивается с табличным значением уровня значимости α для k(k-1)/2 степеней свободы.

Одним из методов снижения мультиколлинеарности системы объясняющих переменных X₁, X₂, …, X_k является выявление пар переменных с высокими коэффициентами корреляции (более 0,8). При этом одну из таких переменных исключают из рассмотрения. Какую из двух переменных удалить решают на основании экономических соображений или оставляют ту, которая имеет более высокий коэффициент корреляции с зависимой переменной.

Полезно также находить множественные коэффициенты корреляции между одной объясняющей переменной и некоторой группой из них.

Множественный коэффициент корреляции служит мерой линейной зависимости между случайной величиной Х_i и некоторым набором других случайных величин X₁, X₂, X₃, …,X_i-1,X_i+1,… X_k.

Множественный коэффициент корреляции определяется как обычный коэффициент парной корреляции между Х_i и Х_i^*, где Х_i^*− наилучшее линейное приближение Х_i случайными величинами X₁, X₂, X₃, …,X_i-1,X_i+1,… X_k.

Чем ближе значения коэффициента множественной корреляции к единице, тем лучше приближение случайной величины Х_i линейной комбинацией случайных величин X₁, X₂, X₃, …,X_i-1,X_i+1,… X_k.

Множественный коэффициент корреляции выражается через элементы корреляционной матрицы следующим образом:

, (2.7.2)

где ǀRǀ – определитель корреляционной матрицы R;

R_ii – алгебраическое дополнение элемента r_ii.

Если , то величина Х_i представляет собой линейную комбинацию случайных величин X₁, X₂, X₃, …,X_i-1,X_i+1,… X_k.

С другой стороны, только тогда, когда Х_i не коррелированна ни с одной из случайных величин X₁, X₂, X₃, …,X_i-1,X_i+1,… X_k.

В качестве выборочной оценки коэффициента множественной корреляции используется выражение

_(2.7.3)

Наличие высокого множественного коэффициента корреляции (более 0,8) также свидетельствует о мультиколлинеарности.

Еще одним из методов уменьшения мультиколлинеарности является использование пошаговых процедур отбора наиболее информативных переменных с использованием скорректированного коэффициента детерминации.

Недостатком коэффициента детерминации R² для выбора наилучшего уравнения регрессии является то, что он всегда увеличивается при добавлении новых переменных в регрессионную модель. Поэтому целесообразно использовать скорректированный коэффициент детерминации , определяемый по формуле

.

В отличие от R² скорректированный коэффициент может уменьшаться при введении в модель новых объясняющих переменных, не оказывающих существенного влияния на зависимую переменную.

На первом шаге рассматривается лишь одна объясняющая переменная, имеющая с зависимой переменной Y наибольший коэффициент корреляции (детерминации). На втором шаге включается в регрессию новая объясняющая переменная, которая вместе с первоначальной дает наиболее высокий скорректированный коэффициент детерминации с Y и т. д.

Процедура введения новых переменных продолжается до тех пор, пока будет увеличиваться скорректированный коэффициент детерминации

6. ЛИНЕЙНЫЕ РЕГРЕССИОННЫЕ МОДЕЛИ С ПЕРЕМЕННОЙ СТРУКТУРОЙ. ФИКТИВНЫЕ ПЕРЕМЕННЫЕ

До сих пор мы рассматривали регрессионную модель, в которой в качестве объясняющих переменных выступали количественные переменные (производительность труда, себестоимость продукции, доход и т. п.). Однако на практике достаточно часто возникает необходимость исследования влияния качественных признаков, имеющих два или несколько уровней (градаций). К числу таких признаков можно отнести пол (мужской, женский), образование (начальное, среднее, высшее), фактор сезонности (зима, весна, лето, осень) и т.п.

Например, нам надо изучить зависимость размера заработной платы работников Y не только от количественных факторов , но и от качественного признака , например фактора «пол работника».

В принципе можно было бы получить оценки регрессионной модели

(i=1,..,n) (2.8.1)

для каждого уровня качественного признака ( т. е. выборочное уравнение регрессии отдельно для работников-мужчин и отдельно – для женщин), а затем изучать различия между ними.

Но есть и другой подход, позволяющий оценивать влияние количественных переменных и уровней качественных признаков с помощью одного уравнения регрессии. Этот подход связан с введением так называемых фиктивных переменных.

В качестве фиктивных переменных обычно используют дихотомические (булевы) переменные, которые принимают всего 2 значения: 0 или 1 (например, значение такой переменной Z₁ по фактору «пол»: Z₁=0 для работников-женщин и Z₁=1 для мужчин).

В этом случае первоначальная регрессионная модель (2.8.1) заработной платы изменится и примет вид

(i=1,..,n) (2.8.2)

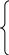
1, если i-й работник мужского пола;

где =

0, если i-й работник женского пола.

Таким образом, принимая модель (2.8.2), мы считаем, что средняя заработная плата у мужчин на *1= выше, чем у женщин, при неизменных значениях других параметров модели. А проверяя гипотезу H₀: =0, мы можем установить существенность влияния фактора «пол» на размер заработной платы работника.

Следует отметить, что в принципе качественное различие можно формализовать с помощью любой переменной, принимающей два разных значения, не обязательно 0 или 1. Однако в эконометрической практике почти всегда используются фиктивные переменные типа «0-1», так как при этом интерпретация полученных результатов выглядит наиболее просто.

Если рассматриваемый качественный признак имеет несколько (k) уровней (градаций), то в принципе можно было бы ввести в регрессионную модель дискретную переменную, принимающую такое же количество значений (например, при исследовании зависимости заработной платы Y от уровня образования Z можно рассматривать k=3 значения: z_i1=1 при наличии начального образования, z_i1=2 – среднего и z_i1=3 при наличии высшего образования). Однако обычно так не поступают из-за трудности содержательной интерпретации соответствующих коэффициентов регрессии, а вводят k-1 бинарных переменных.

В рассматриваемом примере для учета факторов образования можно в регрессионную модель (2.8.2) ввести k-1=3-1=2 бинарные переменные Z₁ и Z₂:

(2.8.3)

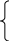
1, если i-й работник имеет высшее образование;

где =

0 во всех остальных случаях.

1, если i-й работник имеет среднее образование;

=

0 во всех остальных случаях.

Третьей бинарной переменной очевидно не требуется, если i-й работник имеет начальное образование, это будет отражено парой значений =0, =0. Более того, вводить третью бинарную переменную Z₃ со значениями , если i-й работник имеет начальное образование; - в остальных случаях, нельзя, так как при этом для любого i-го работника

Это означает линейную зависимость столбцов общей матрицы X, т.е. мы оказались бы в условиях мультиколлинеарности в функциональной форме и как следствие – невозможности получения оценок методом наименьших квадратов.

Пример.

Необходимо исследовать зависимость между результатами письменных вступительных и курсовых экзаменов по математике. Получены следующие данные о числе решенных задач на вступительных экзаменах X (задание – 10 задач) и курсовых экзаменах Y (задание – 7 задач) 12 студентов, а также распределение этих студентов по фактору «пол».

№ студента	Число решенных задач	Число решенных задач	Пол студента	№ студента	Число решенных задач	Число решенных задач	Пол студента
i	xi	yi	zi	i	xi	yi	zi
1	10	6	муж.	7	6	3	жен.
2	6	4	жен.	8	7	4	муж.
3	8	4	муж.	9	9	7	муж.
4	8	5	жен.	10	6	3	жен.
5	6	4	жен.	11	5	2	муж.
6	7	7	муж.	12	7	3	жен.

Построим линейную регрессионную модель Y по X с использованием фиктивной переменной по фактору «пол». Для ее учета введем в регрессионную модель фиктивную бинарную переменную Z.

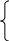
1, если i-ый студент мужского пола;

z_i=

0, если i-ый студент женского пола.

Таким образом, мы получили регрессионную модель

с общей матрицей

1 1 1 1 1 1 1 1 1 1 1 1

Х^T = 10 6 8 8 6 7 6 7 9 6 5 7

1. 0 1 0 0 1 0 1 1 0 1 0

По формуле (2.6.3) найдем вектор оценок параметров регрессии

Таким образом, выборочное уравнение множественной регрессии примет вид

(2.8.4)

Коэффициент детерминации .

Уравнение регрессии значимо по F-критерию при 5%-ном уровне значимости, так как в соответствии с (2.6.12)

Из (2.8.4) следует, что при том же числе решенных задач на вступительных экзаменах Х, на курсовых экзаменах юноши решают в среднем на 0,466≈0,5 задачи больше.

Полученное уравнение множественной регрессии значимо по – критерию. Однако коэффициент регрессии β₁ при фиктивной переменной Z незначим по t- критерию

Следовательно, по имеющимся данным влияние фактора «пол» оказалось несущественным, и у нас есть основание считать, что регрессионная модель результатов курсовых экзаменов по математике в зависимости от вступительных одна и та же для юношей и девушек.

6. НЕЛИНЕЙНЫЕ МОДЕЛИ РЕГРЕССИИ

До сих пор мы рассматривали линейные регрессионные модели, в которых переменные имели первую степень (модели, линейные по переменным), а параметры выступали в виде коэффициентов при этих переменных (модели, линейные по параметрам). Однако соотношения между экономическими переменными далеко не всегда можно выразить линейными функциями.

Так, например, нелинейными оказываются производственные функции (зависимости между объемом произведенной продукции и основными факторами производства – трудом и капиталом).

Для оценки параметров нелинейных моделей используются два подхода.

Первый подход основан на линеаризации модели и заключается в том, что с помощью подходящих преобразований исходных переменных исследуемую зависимость представляют в виде линейного соотношения между преобразованными переменными.

Второй подход применяется в случае, когда подобрать соответствующее линеаризующее преобразование не удается. В этом случае применяются методы нелинейной оптимизации на основе исходных переменных.

Для линеаризации модели в рамках первого подхода могут использоваться как модели, не линейные по переменным, так и не линейные по параметрам.

Если модель нелинейна по переменным, то введением новых переменных ее можно свести к линейной модели, для оценки параметров которой использовать обычный метод наименьших квадратов.

Так, например, если необходимо оценить параметры регрессионной модели

(i=1,…,n)

то вводя новые переменные , получим линейную модель

, (i=1,…,n)

параметры которой находятся обычным методом наименьших квадратов.

Более сложной проблемой является нелинейность модели по параметрам, так как непосредственное применение метода наименьших квадратов для их оценивания невозможно. К числу таких моделей можно отнести, например, мультипликативную модель

, (i=1,..,n) (2.9.1)

экспоненциальную модель

(i=1,..,n) (2.9.2)

и другие.

В ряде случаев путем подходящих преобразований эти модели удается привести к линейной форме. Так, модели (2.9.1) и (2.9.2) могут быть приведены к линейным логарифмированием обеих частей уравнений. Тогда, например, модель (2.9.1) примет вид

(i=1,..,n) (2.9.3)

К модели (2.9.3) уже можно применять обычные методы исследования линейной регрессии. Следует однако отметить и недостаток такой замены, связанный с тем, что вектор оценок получается не из условия минимизации суммы квадратов отклонений для исходных переменных, а из условия минимизации суммы квадратов отклонений для преобразованных переменных, что не одно и то же. Следует также подчеркнуть, что критерии значимости и интервальные оценки параметров, применимые для нормальной линейной регрессии, требуют, чтобы нормальный закон распределения в моделях (2.9.1), (2.9.2) имел логарифм вектора возмущений а вовсе не ε.

Заметим попутно, что к модели

(i=1,..,n) (2.9.4)

изложенные методы уже непригодны, так как модель (2.9.4) нельзя привести к линейному виду.

В качестве примера использования линеаризирующего преобразования регрессии рассмотрим производственную функцию Кобба-Дугласа

(2.9.5)

где - объем производства, - затраты капитала, - затраты труда.

Учитывая влияние случайных возмущений, присущих каждому экономическому явлению, функцию Кобба-Дугласа (2.9.5) можно представить в виде

(2.9.6)

Полученную мультипликативную модель легко свести к линейной путем логарифмирования обеих частей уравнения (2.9.6). Тогда для i-го наблюдения получим

= + (i=1,..,n) (2.9.7)

6. ОБОБЩЕННАЯ ЛИНЕЙНАЯ МОДЕЛЬ. ГЕТЕРОСКЕДАСТИЧНОСТЬ ОСТАТКОВ.

При моделировании реальных экономических процессов мы нередко сталкиваемся с ситуациями, в которых условия классической линейной модели регрессии оказываются нарушенными. В частности, могут не выполняться предпосылки регрессионного анализа о том, что случайные ошибки модели имеют постоянную дисперсию и не коррелированны между собой. Для линейной множественной модели эти предпосылки означают, что ковариационная матрица вектора возмущений (ошибок) ε имеет вид

. (2.10.1)

В тех случаях, когда имеющиеся статистические данные достаточно однородны, допущение (2.10.1) вполне оправдано. Однако, в других ситуациях оно может оказаться неприемлемым. Так, например, при исследовании зависимости расходов на потребление от уровня доходов семей можно ожидать, что в более обеспеченных семьях вариация расходов выше, чем в малообеспеченных, то есть дисперсии возмущений не одинаковы.

Обобщенная линейная модель множественной регрессии

(2.10.2)

отличается от классической только видом ковариационной матрицы: вместо

для классической модели имеем для обобщенной.

Для оценки параметров модели (2.10.2) можно применить обычный метод наименьших квадратов.

Оценка _{, полученная ранее и определенная соотношением (2.6.3), остается справедливой и в случае обобщенной модели. Оценка по-прежнему несмещенная и состоятельная.}

_{Однако, полученная ранее формула для ковариационной матрицы вектора оценок Σ оказывается неприемлемой в условиях обобщенной модели. Действительно, учитывая (2.6.7), получим для обобщенной модели}

,

(2.10.3)

в то время как для классической модели имели по формуле (2.6.8)

_(2.10.4)

_{Обычный метод наименьших квадратов в обобщенной линейной регрессионной модели дает смещенную оценку ковариационной матрицы вектора оценок Σ.}

Оценка , определенная по (2.6.3), хотя и будет состоятельной и несмещенной, но не будет оптимальной. Для получения эффективной оценки нужно использовать другую оценку, получаемую так называемым обобщенным методом наименьших квадратов.

Согласно теореме Айткена, в классе линейных несмещенных оценок вектора для обобщенной регрессионной модели оценка

_(2.10.5)

имеет наименьшую ковариационную матрицу.

На практике ковариационная матрица возмущений 𝛺 почти никогда не известна и оценить ее параметров по n наблюдениям не представляется возможным.

Тест Гольдфельда-Квандта на гомоскедастичность.

Этот тест применяется в том случае, если ошибки регрессии можно считать нормально распределенными случайными величинами.

Предположим, что средние квадратичные отклонения возмущений пропорциональны значениям объясняющей переменной Х (это означает постоянство часто встречающегося на практике относительного а не абсолютного, как в классической модели, разброса возмущений регрессионной модели).

Упорядочим n наблюдений в порядке возрастания значений Х и выберем m первых и m последних наблюдений.

В этом случае гипотеза о гомоскедастичности будет равносильна тому, что значения и , , то есть остатки регрессии первых и последних m наблюдений, представляют собой выборочные наблюдения нормально распределенных случайных величин, имеющих одинаковые дисперсии.

Гипотеза о равенстве дисперсий двух нормально распределенных совокупностей проверяется с помощью критерия Фишера.

Нулевая гипотеза о равенстве дисперсий двух наборов по m наблюдений, то есть гипотеза о гомоскедастичности отвергается, если

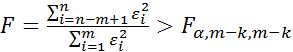, (2.10.6)

где k – число независимых переменных модели.

Мощность теста, то есть вероятность отвергнуть гипотезу о гомоскедастичности, когда действительно гомоскедастичности нет, оказывается максимальной, если выбирать m порядка n/3.

Пример. По данным n=150 наблюдений о доходе индивидуума Y, уровне его образования X₁ и возрасте X₂ выяснить, можно ли считать на уровне значимости α=0,05 линейную регрессионную модель Y по X₁ и X₂ гомоскедастичной.

Возьмем по m=n/3=150/3=50 значений доходов лиц с наименьшим и наибольшим уровнем образования X₁.

Вычислим суммы квадратов остатков

= .

По таблице распределения Фишера находим, что

Это означает, что гипотеза о гомоскедастичности должна быть отвергнута.

Задание № 1.

В табл. 1 приведены 5 показателей деятельности торговых предприятий. В соответствии с таблицей выберите номера 2-х показателей

Номер варианта	Номер 1-го показателя	Номер 2-го показателя
1	1	2
2	1	3
3	1	4
4	1	5
5	2	3
6	2	4
7	2	5
8	3	4
9	3	5
10	4	5

Т а б л и ц а 1 Показатели деятельности торговых предприятий за год

Номер предпри-ятия	Численность работников	Средняя зарплата, тыс. р.	Дебиторская задолженность на конец года, тыс. р.	Балансовая прибыль, тыс. р.	Собственные оборотные средства, тыс. р.
1	20	17,3	7,0	80	320
2	50	20,2	5,1	105	611
3	80	19,1	1,2	100	840
4	35	17,0	7,1	94	482
5	115	20,3	2,2	112	1050
6	40	19,1	5,3	108	499
7	40	19,2	4,0	100	505
8	50	19,2	4,1	88	521
9	30	17,0	7,8	92	412
10	35	17,1	7,3	90	405
11	70	19,3	2,2	92	788
12	120	21,0	1,0	101	1280
13	100	20,0	2,3	98	990
14	70	19,7	7,4	95	810
15	65	19,2	5,6	90	750
16	80	19,1	2,0	95	924
17	150	21,3	1,5	109	1950
18	50	18,0	5,3	90	590
19	60	20,0	3,2	97	722
20	50	19,1	5,8	90	540
21	60	19,0	5,0	87	700
22	90	20,7	5,6	100	980
23	40	19,6	6,5	98	490
24	25	20,5	5,3	89	375
25	85	18,3	3,7	90	910
26	75	19,2	4,8	97	845
27	175	21,8	4,9	108	2400
28	100	20,9	2,1	102	1100
29	40	18,2	7,0	88	470
30	50	18,0	6,8	96	588

С помощью корреляционного и регрессионного анализа изучить связь между показателями, указанными в Вашем варианте.

1. Рассчитать значение коэффициента корреляции для

данных табл. 1.

2. Сделать вывод о тесноте статистической связи.

3. Найти коэффициенты парной линейной регрессии и сделать прогноз признака-результата, если признак-фактор принимает свое среднее значение.

2. СИСТЕМЫ ОДНОВРЕМЕННЫХ УРАВНЕНИЙ

1. СИСТЕМЫ НЕЗАВИСИМЫХ И ВЗАИМОСВЯЗАННЫХ (СОВМЕСТНЫХ) УРАВНЕНИЙ

Сложные экономические процессы описываются с помощью системы взаимосвязанных (одновременных) уравнений.

Различают несколько видов систем уравнений.

1. Система независимых уравнений, когда каждая зависимая переменная Y_i (i=1,…,n) рассматривается как функция одного и того же набора факторов X_j (j=1,…,m).

………..

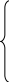
Для нахождения параметров этих моделей используется метод наименьших квадратов.

2. Система совместных (взаимозависимых) уравнений, когда одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других – в правую.

…………

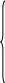
Переменные, определяемые внутри системы Y_i (i=1,…,n), называются эндогенными, а переменные, определяемые вне системы X_j (j=1,…,m)– экзогенными. Кроме экзогенных переменных в системе могут быть эндогенные переменные, относящиеся к предыдущим моментам времени (эндогенные переменные с временным лагом). Экзогенные переменные и эндогенные переменные с временным лагом называются предопределенными переменными, так как значения этих переменных известны к текущему моменту времени.

Пример.

Рассмотрим систему одновременных уравнений

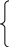(3.1.1)

,

где y₁ – спрос-предложение;

y₂ – цена;

х₁ – уровень доходов.

В рассматриваемой модели цена и спрос-предложение рассматриваются как эндогенные переменные, а доход – как экзогенная переменная. Предполагается, что экзогенные переменные определяются вне системы и поэтому не коррелируют со случайными компонентами, отражающим влияние неучтенных факторов. Эндогенные переменные, определяемые из уравнений системы, имеют ненулевую корреляцию со случайными компонентами.

Действительно, разрешая уравнения относительно эндогенных переменных, получим

Отсюда

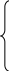
(3.1.2)

.

Нетрудно убедиться, что и _.

Таким образом, нарушаются основные предположения регрессионного анализа, что приводит к потере свойств оценок, получаемых методом наименьших квадратов (появляется смещенность и исчезает состоятельность оценок). Поэтому непосредственное применение метода наименьших квадратов приводит к грубым ошибкам.

2. СТРУКТУРНАЯ И ПРИВЕДЕННАЯ ФОРМЫ ЭКОНОМЕТРИЧЕСКОЙ МОДЕЛИ. УСЛОВИЯ ИДЕНТИФИКАЦИИ.

Система уравнений (3.1.1) называется структурной формой модели, а ее коэффициенты – структурными коэффициентами. Система (3.1.2) называется приведенной формой модели.

Обозначим

; ; ; .

Тогда систему уравнений (3.1.2) можно переписать в виде

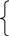(3.2.1)

.

В системе (3.2.1) объясняющая переменная х₁ является экзогенной переменной и, следовательно, независима со случайными компонентами v₁ и v₂. Метод наименьших квадратов дает состоятельные оценки и .

Очевидно, что . Можно показать, что будет состоятельной оценкой структурного коэффициента .

Такой метод построения оценок структурных коэффициентов с помощью оценок коэффициентов приведенной формы называется косвенным методом наименьших квадратов.

Вместе с тем, коэффициенты и не могут быть найдены, т. е. они неидентифицируемые.

В общем случае под идентифицируемостью понимают возможность определения структурных коэффициентов уравнений по коэффициентам приведенной формы.

Проблема идентификации – это проблема единственности соответствия между приведенной и структурной формами. Приведенная форма в полном виде имеет nm параметров, а структурная – n(n-1+m) параметров. Ясно, что n(n-1+m) оценок параметров структурной формы в общем случае невозможно получить единственным образом на основе nm параметров приведенной формы.

Необходимое условие идентифицируемости – выполнение следующего правила:

- уравнение идентифицируемое;

- уравнение неидентифицируемое;

- уравнение сверх идентифицируемое,

где Н – число эндогенных переменных в уравнении;

D – число предопределенных переменных системы, отсутствующих в уравнении.

Для сверх идентифицированных уравнений используется двухшаговый метод наименьших квадратов, который заключается в следующем:

- составляют приведенную форму модели и определяют ее параметры обычным МНК;

- выявляют эндогенные переменные, находящиеся в правой части структурного уравнения, и находят их расчетные значения по соответствующим уравнениям приведенной формы модели;

- обычным МНК определяют параметры структурного уравнения, используя в качестве исходных данных расчетные значения эндогенных переменных, стоящих в правой части структурного уравнения.

Пример.

Имеется следующая система структурных уравнений

.

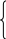
Приведенная система уравнений после оценки параметров методом наименьших квадратов имеет вид

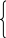
Для первого уравнения H=2, D=1 (отсутствует х₄) и , т. е. уравнение является идентифицируемым.

Для второго уравнения H=2, D=1 (отсутствует х₂) и , т. е. уравнение также является идентифицируемым.

Чтобы получить первое структурное уравнение из 1-го приведенного, выразим отсутствующий признак х₄ из 2-го приведенного уравнения:

После подстановки х₄ в первое приведенное уравнение и преобразований, получим

.

Для определения параметров 2-го структурного уравнения выразим отсутствующий во 2-ом структурном уравнении фактор х₂ из 1-го приведенного уравнения

После подстановки х₂ во второе приведенное уравнение, получим

Задание № 2.

Построить модель вида

,

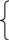
рассчитав соответствующие структурные коэффициенты.

Система приведенных уравнений имеет вид

Значения коэффициентов приведены в таблице

Номер варианта
1	0,006	-0,265	0,003	0,112
2	0,005	-0,308	0,002	0,115
3	0,006	-0,250	0,003	0,128
4	0,005	-0,275	0,002	0,117
5	0,006	-0,283	0,003	0,127
6	0,005	-0,301	0,003	0,110
7	0,006	-0,255	0,002	0,118
8	0,005	-0,315	0,002	0,131
9	0,006	-0,245	0,002	0,113
10	0,005	-0,270	0,003	0,126

3. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ И ПРОГНОЗИРОВАНИЕ

1. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ

Временной ряд представляет собой ряд числовых значений какого-либо показателя в последовательные моменты или периоды времени. Числовые значения, составляющие временной ряд, называются уровнями ряда.

По способу построения ряд может быть моментным, когда уровни ряда представлены на определенные моменты времени (конец квартала, начало года и т.д.) и интервальным, когда уровни ряда соответствуют определенным интервалам времени.

Изучение различных процессов на основе временных рядов включает следующие этапы:

- сбор исходной информации и построение временных рядов;

- визуальный анализ временного ряда и формирование набора возможных моделей прогнозирования;

- идентификация (подбор) модели;

- оценка параметров моделей;

- осуществление прогноза по математической модели.

В практике анализа временных рядов принято считать, что значения уровней временных рядов складываются из следующих компонент:

- тренд;

- сезонная составляющая;

- циклическая составляющая;

- случайная составляющая.

Под трендом (тенденцией) понимают изменения, определяющие общее направление развития изучаемого показателя. Это систематическая составляющая долговременного действия. Для описания тренда используют плавно меняющиеся, гладкие функции.

Наряду с долговременными тенденциями во временных рядах часто имеют место более или менее регулярные колебания – периодические составляющие рядов динамики. Если период колебаний не превышает одного года, то их называют сезонными. Причины сезонных колебаний могут быть связаны с природно-климатическими условиями, могут носить социальный характер (например, увеличение покупок в выходные дни, увеличение платежей в конце квартала и т. д.). Для описания сезонной компоненты используют периодические функции.

При большом периоде колебаний считают, что во временных рядах имеется циклическая составляющая. Примерами могут служить демографические, деловые, инвестиционные и другие циклы.

Если из временного ряда удалить тренд и периодические составляющие, то останется нерегулярная компонента. Часто причиной нерегулярных колебаний является действие большого числа различных факторов. Эта компонента рассматривается как случайная.

2. КРИТЕРИЙ СЛУЧАЙНОСТИ

Одним из первых вопросов при анализе временного ряда является вопрос о наличии или отсутствии тренда. Для решения этого вопроса со статистических позиций используют различные тесты на случайность.

Один из наиболее простых критериев состоит в подсчете количества «пиков» или «ям» в ряде. «Пик» есть значение, которое больше двух соседних, а «яма» - значение, которое меньше двух соседних. «Пики» и «ямы» называются экстремальными точками или «точками поворота». Интервал монотонности между двумя экстремальными точками называют «фазой».

Чтобы определить экстремальную точку требуется 3 последовательных уровня ряда. Если бы ряд был случаен, то вероятность появления экстремальной точки была бы равна 2/3 (четыре варианта из 3!).

Рассмотрим временной ряд и введем переменную следующим образом (i=1,2, …, n-2):

, если или ;

, в противном случае.

Тогда число экстремальных точек

_.

В предположении случайности ряда математическое ожидание случайной величины Р составит

.

Кроме того, можно показать, что

.

3. ПОКАЗАТЕЛИ ДИНАМИКИ ВРЕМЕННЫХ РЯДОВ

Показатели динамики – это величины, характеризующие изменения уровней временного ряда. К ним относятся абсолютный прирост, коэффициент (темп) роста и коэффициент (темп) прироста.

Различают базисные и цепные показатели динамики. Базисные показатели – это результат сравнения текущего уровня ряда с одним фиксированным уровнем, принятым за базу (обычно это начальный уровень ряда). Цепные показатели – это результат сравнения текущего уровня ряда с предшествующим уровнем.