6. Полиномиальные модели прогнозирования

Полиномиальная модель зависимости прогнозируемого показателя от времени имеет вид

(4.6.1)

где a_i – параметры модели (i=0,…,m);

t – время:

m – степень полинома.

Согласно модели (4.6.1) для фактических данных (i=1,..,n) имеют место следующие соотношения

(i=1,…,n).

Эти соотношения можно записать в матричном виде

, (4.6.2)

– вектор-столбец значений временного ряда;

– вектор-столбец значений параметров модели;

- вектор-столбец случайных ошибок;

T=

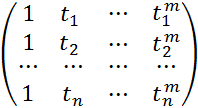
Оценки параметров а₀, a₁, … a_m можно получить с помощью рассмотренного ранее метода наименьших квадратов.

Система уравнений имеет вид

,

,

……..

.

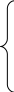Суммирование производится по индексу i от 1 до n, где n – количество точек (уровней) в динамическом ряду.

Эту систему обычно записывают в матричном виде

,

где - транспонированная матрица ;

Отсюда

. (4.6.3)

Оценки, полученные с помощью МНК, являются случайными величинами, так как представляют собой линейную комбинацию случайных величин у₁, у₂, … у_n.

Найдем математическое ожидание и дисперсию оценок параметров (i=0,…,m). Из (4.6.2) следует, что

.

Так как М()=0, то и

.

Таким образом, оценки являются несмещенными.

Найдем ковариационную матрицу оценок

.

В этой матрице элементами главной диагонали являются дисперсии оценок .

Выполним преобразование

,

откуда .

Тогда

.

Полученное выражение содержит матрицу

M(^T) =

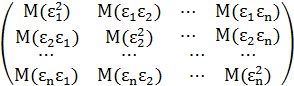
В данной матрице все элементы, не лежащие на главной диагонали, равны 0 (в силу предположения о некоррелированности ошибок _i). Поскольку все ошибки имеют одинаковую дисперсию, то

,

где Е – единичная матрица.

Окончательно получим

. (4.6.4)

Так как величина ² неизвестна, в качестве ее оценки используется величина

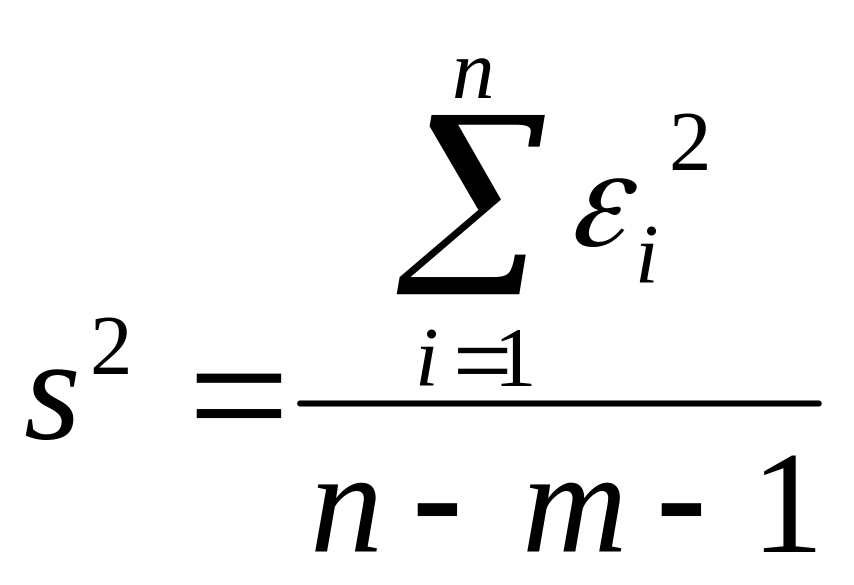. (4.6.5)

Определим теперь дисперсию ошибки прогноза. Если t_L – прогнозный момент времени, то прогноз по полиномиальной модели имеет вид

.

Отметим, что

,

т. е. мы получили несмещенный прогноз среднего уровня

+

+

Это выражение можно записать в матричной форме

,

где T^T_L= ( 1 t_L t_L² …… t_L^m ).

Учитывая (4.6.4), получим

.

Поскольку ² неизвестна, будем использовать ее оценку

.

Ошибка прогноза обусловлена не только ошибкой оценки среднего, но и случайным отклонением от среднего уровня

,

где – истинное значение среднего уровня.

Тогда

= .

Окончательно

. (4.6.6)

ПРИМЕР. Динамика объема продаж некоторого товара (тыс.шт.) за 9 лет приведена в табл. 4.3.

Таблица 4.3.

Год	ti	yi	tiyi	ti^2	yiti^2	ti^3	ti^4	(t)
1995	1	18,2	18,2	1	18,2	1	1	17,6
1996	2	20,1	40,2	4	80,4	8	16	20,9
1997	3	23,4	70,2	9	210,6	27	81	23,3
1998	4	24,6	98,4	16	393,6	64	256	24,1
1999	5	25,6	128,0	25	640,0	125	625	25,5
2000	6	25,9	155,4	36	932,4	216	1296	25,3
2001	7	23,6	165,2	49	1156,4	343	2401	24,2
2002	8	22,7	181,6	64	1452,8	512	4096	22,3
2003	9	19,2	172,8	81	1555,2	729	6561	19,4
Cумма	45	203,3	1030,0	285	6439,6	2025	15333	203,3

Из таблицы видно, что в течение первых 6 лет объем продаж товара возрастал, а в последние 3 года снижался. Это говорит о невозможности аппроксимации временного ряда линейной зависимостью.

Попробуем описать динамику полиномом 2-го порядка (параболой)

.

Система уравнений для оценки параметров полинома 2-го порядка имеет вид:

,

,

.

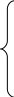Для нашего примера (см. итоговую строку таблицы):

,

,

.

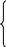
Решение этой системы дает коэффициенты полинома

,

а математическая модель принимает вид

.

Полученные с ее помощью «прогнозы» (для t=1,…,9) приведены в последнем столбце таблицы. Нетрудно заметить, что они достаточно близки к реальным данным.

7. СТАЦИОНАРНЫЕ ВРЕМЕННЫЕ РЯДЫ. АВТОКОРРЕЛЯЦИОННАЯ ФУНКЦИЯ.

Важное значение в анализе временных рядов имеют стационарные временные ряды, вероятностные свойства которых не изменяются во времени.

Случайным процессом Y(t) называется функция от t, которая при любом значении t является случайной величиной.

Временной ряд можно рассматривать как одну из реализаций (траекторий) случайного процесса Y(t).

Временной ряд называется строго стационарным (или стационарным в узком смысле), если совместное распределение вероятностей случайных величин

точно такое же, как и для случайных величин

для любых t,τ и n.

Для стационарных временных рядов определяют степень тесноты связи между Y(t) и

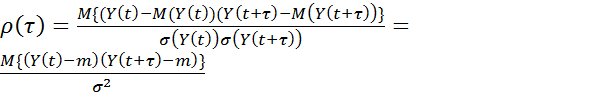
ибо

,

.

Зависимость называют автокорреляционной функцией. В силу стационарности временного ряда автокорреляционная функция зависит только от лага τ.

Под стационарным процессом в широком смысле понимают случайный процесс, у которого среднее и дисперсия не зависят от t, а автокорреляционная функция зависит только от длины лага между рассматриваемыми переменными

,

,

,

где

Основная проблема в оценивании параметров случайного процесса состоит в том, что фактически имеется только одна его реализация. Данную проблему можно решить с использованием понятия эргодичности – замены усреднения по множеству реализаций случайного процесса усреднением по времени. Эргодичность делает возможным оценивание только по одной его реализации – временному ряду.

Оценка математического ожидания

=

Оценка дисперсии

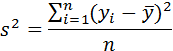
Оценка автокорреляции (выборочный коэффициент автокорреляции )

=

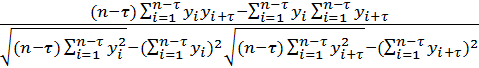
Функцию называют выборочной корреляционной функцией, а ее график – коррелограммой. При расчете следует помнить, что с увеличением τ число n-τ пар наблюдений уменьшается, поэтому лаг должен быть таким, чтобы число n-τ было достаточным для определения . Обычно .

8. АДАПТИВНЫЕ МОДЕЛИ ПРОГНОЗИРОВАНИЯ

При прогнозировании стационарных процессов используются так называемые адаптивные модели, к числу которых относятся модели экспоненциального сглаживания и модель Бокса-Дженкинса, которая является более общей по отношению к модели экспоненциального сглаживания.

Экспоненциальное сглаживание

Экспоненциальное сглаживание временного ряда y_t осуществляется по рекуррентной формуле

, (4.8.1)

где S_t- значение экспоненциальной средней в момент времени t;

a – параметр сглаживания (0<a<1);

=1-a.

Выражение (4.8.1) можно переписать следующим образом

(4.8.2)

В формуле (4.8.2) экспоненциальная средняя на момент времени t выражена как сумма экспоненциальной средней предшествующего периода S_t-1 и доли a разницы текущего значения временного ряда y_t и экспоненциальной средней S_t-1.

Последовательное применение рекуррентной формулы (4.8.1) приводит к следующему выражению для S_t

_,

где n – число точек временного ряда;

S₀ - некоторая начальная величина, необходимая для первого

применения формулы (4.8.1).

Так как <1, то при n , а сумма коэффициентов и

, (4.8.3)

т.е. S_t оказывается взвешенной суммой всех уровней временного ряда. При этом веса падают экспоненциально с возрастанием «возраста» данных.

Рассмотрим стационарный процесс следующего вида

.

Для такого процесса

(4.8.4)

Найдем математическое ожидание и дисперсию S_t, воспользовавшись формулой (4.8.4).

Так как , то

.

Таким образом, экспоненциальная средняя S_t имеет то же математическое ожидание, что и y_t , но меньшую дисперсию.

Экспоненциальная средняя S_t может быть использована не только для сглаживания временного ряда, но и для краткосрочного прогнозирования.

Прогнозная модель имеет вид

,

где - прогноз, сделанный в момент времени t на  единиц времени вперед.

Отметим, что все свойства экспоненциальной средней распространяются на прогнозную модель. В частности, если S_t-1 рассматривать как прогноз на 1 шаг вперед в момент времени t-1, то величина y_t-S_t-1 представляет собой погрешность этого прогноза, а новый прогноз S_t получается в результате корректировки предыдущего прогноза с учетом его ошибки по формуле (4.8.2). В этом и состоит суть адаптации.

При краткосрочном прогнозировании желательно с одной стороны быстро отразить изменение среднего уровня, а с другой – очистить ряд от случайных колебаний.

Для выполнения первого требования величину a следует увеличить, а для выполнения второго – уменьшить. Таким образом, эти два требования находятся в противоречии и необходим некий компромисс.

Рассмотрим вопрос выбора параметра a. При S_t= S₀, т.е. адаптация полностью отсутствует, а при имеет место так называемая «наивная» модель прогнозирования

,

в соответствии с которой прогноз на любой срок равен текущему (последнему) значению временного ряда. В ряде работ рекомендовано брать значение a в пределах от 0,1 до 0,3, однако эта рекомендация по сути не имеет должного обоснования.

Выбор начального значения S₀ всегда вызывает вопрос, однако если параметр a велик, то величина быстро убывает с ростом i и влияние S₀ на величину S_t становится несущественным.

ПРИМЕР

Для иллюстрации процедуры расчета экспоненциальной средней рассмотрим пример сглаживания динамики курса акций фирмы IBM, производящей ЭВМ (табл. 4.4).

Табл.4.4

Экспоненциальные средние

Номер точки	Исход-ный ряд				Номер точки	Исход-ный ряд
1	510	506,4	508,0	509,6	16	512	505,7	513,3	513,1
2	497	505,5	502,5	498,3	17	510	506,1	511,7	510,3
3	504	505,3	503,2	503,4	18	506	506,1	508,8	506,4
4	510	505,8	506,6	509,3	19	515	507,0	511,9	514,1
5	509	506,1	507,8	509,0	20	522	508,5	517,0	521,2
6	503	505,8	505,4	503,6	21	523	509,9	520,0	522,8
7	500	505,2	502,7	500,4	22	527	511,6	523,5	526,6
8	500	504,7	501,4	500,0	23	523	512,8	523,2	523,4
9	500	504,2	500,7	500,0	24	528	514,3	525,6	527,5
10	495	503,3	497,8	495,5	25	529	515,8	527,3	528,9
11	494	502,4	495,9	494,2	26	538	518,0	532,7	537,1
12	499	502,0	497,5	498,5	27	539	520,1	525,8	538,8
13	502	502,0	499,7	501,2	28	541	522,2	538,4	540,8
14	509	502,7	504,4	508,3	29	543	524,3	540,7	542,8
15	525	505,0	514,7	523,3	30	541	525,9	540,9	541,2

При проведении расчетов начальное значение экспоненциальной средней S₀ было принято равным средней арифметической из первых 5 уровней ряда

В нашем случае

Дальнейшие вычисления при выглядят следующим образом

и т. д.

Результаты вычислений экспоненциальных средних при a=0,1, a=0,5 и a=0,9 приведены в табл. 4.4.

Модели Бокса-Дженкинса

Рассмотрим ряд частных моделей Бокса-Дженкинса для стационарного процесса c нулевым математическим ожиданием. Если математическое ожидание процесса не равно нулю ( , то вычитая это значение из всех значений временного ряда, можно получить временной ряд с нулевым математическим ожиданием.

А) Модель скользящего среднего 1-го порядка СС(1)

Модель скользящего среднего 1-го порядка имеет вид

(4.8.5)

где - некоррелированная случайная величина с

нулевым математическим

ожиданием ( и постоянной

дисперсией ( );

– параметр модели.

Нетрудно видеть, что процесс СС(1) обладает следующими свойствами:

При

Аналогично при всех остальных τ (2,3,…) .

Б) Модель скользящего среднего q-го порядка СС(q)

Модель скользящего среднего q-го порядка имеет вид

(4.8.6)

Процесс СС(q)обладает следующими свойствами

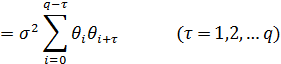
при .

В) Модель авторегрессии 1-го порядка

Модель авторегрессии 1-го порядка имеет вид

(4.8.7)

Предположим, что этот процесс стационарный с нулевым математическим ожиданием.

Тогда

и

Отсюда

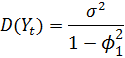
Таким образом,

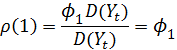
Можно показать, что в общем виде для автокорреляционной функции процесса авторегрессии первого порядка будет иметь место следующая зависимость

Таким образом, автокорреляционная функция убывает по геометрической прогрессии.

Г) Модель авторегрессии p-го порядка

Модель авторегрессии порядка p – АР(p) имеет вид

(4.8.8)

Для компактного описания этого процесса введем понятие оператора сдвига назад B: ; ; …. .

Тогда математическая модель может быть записана в следующем виде

(4.8.9)

где . (4.8.10)

Процесс авторегрессии не всегда стационарен. Вопрос о стационарности процесса авторегрессии можно выяснить с помощью так называемого характеристического уравнения

(4.8.11)

Если все комплексные корни характеристического уравнения лежат вне единичного круга, то есть , то процесс авторегрессии является стационарным. Отметим, что данное требование является обязательным.

Пример. Процесс авторегрессии первого порядка имеет характеристическое уравнение с корнем Так как , то процесс стационарен. Его значения колеблются вокруг нуля.

Процесс авторегрессии первого порядка имеет характеристическое уравнение с корнем Так как , то процесс не стационарен. Коэффициент 1,1 приводит к постоянному увеличению последующих значений процесса.

Для процесса авторегрессии диагностической функцией ее порядка является так называемая частная автокорреляционная функция (ЧАК).

Предположим, что описывается процессом авторегрессии порядка τ

(4.8.12)

При этом последний коэффициент называется коэффициентом частной автокорреляции для величины лага τ.

Ряд ЧАК(τ) называется частной актокорреляционной функцией. Для процесса АР(p) ЧАК(τ)=0 для значений .

Д) Смешанная модель авторегрессии – скользящего среднего порядка (p,q) – АРСС(p,q)

Модель авторегрессии – скользящего среднего порядка (p,q)имеет вид

(4.8.13)

С помощью оператора сдвига назад эта модель может быть записана в компактном виде

(4.8.14)

где

При соблюдении некоторых условий стационарный процесс АРСС(p,q) может быть представлен как бесконечный процесс авторегрессии или бесконечный процесс скользящего среднего

или

(4.8.15)

где

Бесконечный полином определяется выражением

(4.8.16)

В частности, стационарный процесс АР может быть представлен как бесконечный процесс скользящего среднего, а большинство процессов скользящего среднего (при условии обратимости) – как бесконечный процесс авторегрессии . При анализе реальных временных рядов следует выбирать представление процесса с наименьшим возможным числом параметров.

Пример1. Рассмотрим процесс скользящего среднего

Из следует, что и

Из следует, что и и т. д, т.е.

Этот процесс сходится при условии

Пример 2. Рассмотрим стационарный процесс авторегрессии первого порядка

Выразим предшествующий уровень по этой же формуле

. Тогда

Аналогично и +…

Поскольку , этот ряд сходится.

Е) Модели Бокса-Дженкинса для нестационарных рядов

Модели Бокса-Дженкинса могут применяться и для описания нестационарных рядов, которые путем взятия разностей приводятся к стационарным. Например, стационарным может оказаться процесс

Для таких процессов модель Бокса-Дженкинса представляется в виде

(4. 8.17)

где ;

− стационарный процесс, образованный d-й разностью процесса ;

– среднее значение процесса ;

− некоррелированная случайная величина с нулевым математическим ожиданием;

− параметры модели (авторегрессии и скользящего среднего).

Прогнозирование показателей на основе моделей Бокса-Дженкинса включает следующие этапы:

– идентификацию типа модели (определение порядка взятия разности d, числа членов авторегрессии p и скользящего среднего q);

– предварительную оценку параметров модели;

– уточненную оценку параметров модели;

– диагностическую проверку ее адекватности;

– использование модели для прогнозирования, расчет дисперсии ошибок прогноза.

На первом этапе последовательно производится взятие очередной

(d-й) разности исходного временного ряда

_t = ^d = (1-B)^d , (4. 8.18)

где B − оператор сдвига назад (B = );

 − оператор взятия разности ( = - ).

Выбор порядка разности d осуществляется последовательным перебором d=0,1,... до получения минимума дисперсии разностного временного ряда.

Для полученного разностного ряда вычисляются оценки:

– среднего значения

, (4.8.19)

где n = N – d;

N − число точек исходного временного ряда;

– автоковариационной функции

(k = 0,…, n/3); (4. 8.20)

– автокорреляционной функции

(k = 0,…, n/3 ); (4.8.21)

– частной автокорреляционной функции

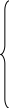
при l=1

=

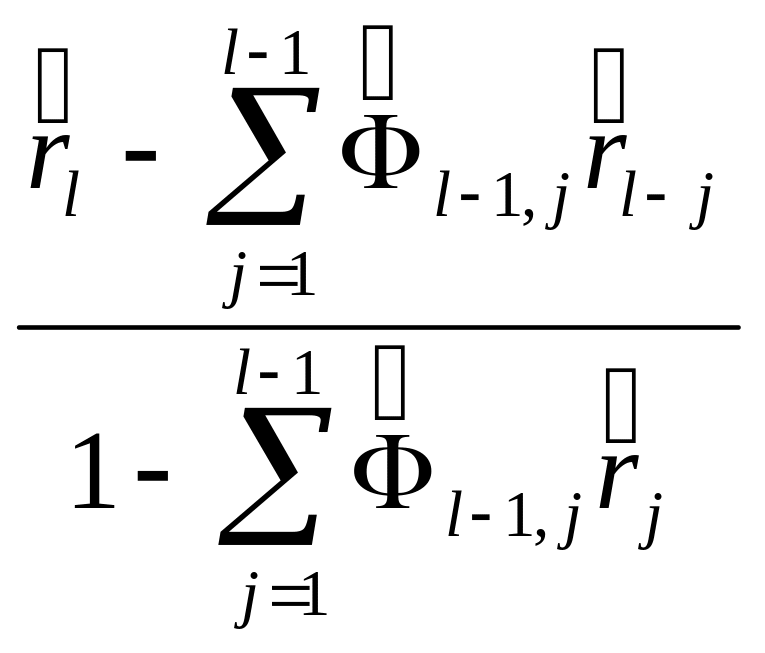(l=2,…, n/3), (4.8.22)

где ( j = 1,…, l-1 ).

Дальнейшая идентификация типа модели (определение параметров p и q) осуществляется на основании анализа поведения автокорреляционной и частной автокорреляционной функций. У процесса авторегрессии порядка p - АР(p) частная автокорреляционная функция равна нулю при k > p, а у процесса скользящего среднего порядка q - СС(q) автокорреляционная функция равна нулю при k > q.

Формула для оценки дисперсии выборочного коэффициента автокорреляции при задержках k, больших q, за которыми автокорреляционная функция процесса СС(q) равна нулю, получена Bartlett M. S. и имеет вид

. (4. 8.23)

Этот результат может использоваться для определения числа членов скользящего среднего q путем статистической проверки гипотезы

Н₀ : r_k=0 (k > q).

Гипотеза не отвергается, если

^{(k > q) . (4. 8.24)}

Отметим, что в формуле (4. 8.24) вместо истинных значений r_i стоят их оценки .

Если q невелико ( q  2 ), то процесс можно описать в виде модели скользящего среднего СС(q).

Определяется число членов авторегрессии - p из условия, что при k > p случайная величина имеет нормальное распределение с нулевым математическим ожиданием и дисперсией D ( )  n . Этот факт можно использовать для статистической проверки гипотезы о равенстве нулю истинных значений Ф_k,k для k > p.

Гипотеза не отвергается, если

(k > p) . (4. 8.25)

Если p невелико ( p 2 ), то процесс можно описать в виде модели авторегрессии АР( p ).

Из величин p и q выбирается наименьшее, и процесс полагается либо СС(q), либо АР(p). Если p=q или p и q достаточно велики, то процесс следует идентифицировать как смешанный процесс АРСС(1,1).

Для решения вопроса идентификации моделей можно использовать ряд критериев:

– информационный критерий Акаике

ИКА (p;q) = n ln S²(p;q) + 2 (p+q);

– байесовский информационный критерий

БИК (p;q) = ln S²(p;q) + (p+q) ln n / n;

– критерий Хеннана-Куина

XK (p;q) = ln S²(p;q) + (p+q) c ln( ln n / n).

Здесь S²(p;q) − оценка дисперсии ² остаточного ряда, а с − некоторая константа (c > 2) .

Процедура подгонки состоит в вычислении критериальной функции для различных значений p и q и выборе тех p и q, при которых величина критериальной функции минимальна.

На втором этапе осуществляется предварительная оценка параметров авторегрессии и скользящего среднего.

Рассмотрим сначала процесс авторегрессии АР(р).



Умножим (4.8.26) на :

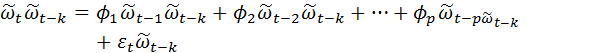
Берем математическое ожидание и получаем разностное уравнение для автоковариации μ( )

Отметим, что когда k>0, так как может включать реализации ε, имевшие место до момента t-k, а они некоррелированы с . Разделив все члены на дисперсию процесса, получим разностное уравнение для автокорреляционной функции

(4.8.27)

Имея коэффициенты автокорреляции, можно с их помощью оценить параметры авторегрессии. Для этого подставим в (4.8.27) k=1,2,..,p и получим систему линейных уравнений для

………………………………………………

(4.8.28)

Система уравнений (4.8.28) называется системой уравнений Юла – Уокера. Заменив теоретические автокорреляции на их оценки , можно получить оценки параметров модели авторегрессии.

Для модели скользящего среднего первоначальная оценка параметров может осуществляться на основе следующих соотношений

(4.8.29)

Задавая k=1,2,..,q , получим систему уравнений, которая является нелинейной относительно оцениваемых параметров и решается с помощью итеративных процедур.

Таким образом, оценка параметров авторегрессии Ф (если р >0) находится из системы p линейных уравнений Юла-Уокера, а оценка параметров скользящего среднего  осуществляется с помощью сложной итеративной процедуры.

На третьем этапе осуществляется уточнение оценок и , полученных на предыдущем этапе, с помощью алгоритма Марквардта, цель которого заключается в минимизации суммы квадратов _t по параметрам и .

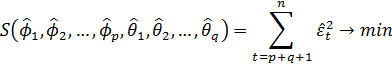
Диагностическая проверка адекватности моделей сводится к проверке статистической гипотезы о некоррелированности случайных величин _t. Для этого могут использоваться критерий Дарбина-Уотсона и совокупный критерий согласия Бокса-Пирса. Этот вопрос будет рассмотрен несколько позже.

На последнем этапе производится вычисление прогнозных значений показателя. Для этого модель

Ф(B) ( 1 - B )^d = (B) _t (4.8.30)

приводится к виду

,

(4.8.31)

где величины _получаются как коэффициенты при B^l в произведении

( 1 - B )^d на Ф(B).

Формула (4.8.31) позволяет прогнозировать y_t рекуррентно для t=t+1, t+2, ...., t+L , где t − текущий момент времени. При этом на i-м шаге в качестве величин y_t+1, y_t+2, ... y_t+i-1 используются их прогнозы, полученные на предыдущих шагах − _t+1, _t+2, ... _t+i-1, а _t+1, _t+2, ... _t+i-1 полагаются равными нулю. Величины ε_t, _t-1, _t-2, ... _t-q определяются на этапе уточненной оценки параметров модели.

Дисперсия ошибок прогноза вычисляется по формуле

, (4.8.32)

где - дисперсия ,

а величины _l определяются по формулам

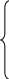₀= 1

₁= __

_{}₂= _₁ __



_l= __l-1 _p+d_l-p-d_l .

При этом _l = 0 для l > q и _l = 0 при l < 0 .

9. МОДЕЛЬ С ЦИКЛИЧНОСТЬЮ РАЗВИТИЯ

Наиболее распространенный подход к построению математических моделей прогнозирования циклических процессов заключается в первоначальном выделении тренда и анализе остаточного ряда в целях выявления и описания периодической компоненты. Для выделения тренда можно использовать процедуру сглаживания временных рядов с помощью метода скользящего среднего.

При анализе сезонных колебаний задача упрощается за счет того, что мы знаем их период – 1 год (это относится и к другим циклическим процессам с постоянным и известным периодом).

Скользящая средняя, применяемая для этой цели, должна иметь строго определенный период скольжения – 12 месяцев или 4 квартала. При этом индекс сезонности можно определить как отношение фактического уровня ряда к уровню, рассчитанному по скользящей средней. Очевидно, что значения индекса сезонности для данного месяца (квартала) будут различаться из года в год. Поэтому в качестве индекса сезонности следует использовать среднее значение индексов, полученных за ряд лет по одноименным месяцам или кварталам.

Однако полученные при этом данные относятся к интервалам с серединами между кварталами, а не к серединам интервалов (15 февраля, 15 мая, 15 августа, 15 ноября). Поэтому необходимо «центрировать» среднее. Наиболее просто это можно сделать, взяв средние последовательных пар средних, вычисленных по 4-м элементам. Такой процесс эквивалентен вычислению средних пяти элементов с весами [ ].

Если средний индекс сезонности за 12 месяцев или 4 квартала не равен единице, производится выравнивание индексов сезонности – деление всех индексов на их средний индекс.

Отметим, что разумно считать, что влияние сезонности носит мультипликативный характер. В этом случае

, (t=1,…,n ; q=1,…,4) (4.9.1)

где s_q – индекс сезонности;

g_t – трендовая составляющая временного ряда.

ПРИМЕР.

В таблице (4.5) представлены поквартальные данные о количестве реализованных единиц товара за три года.

Таблица 5. Данные о реализации товара

Год	Квартал	Период, t	Реализация товара	Тренд	Оценка сезонной компоненты
1	1	1	300	308,5	0,972
	2	2	320	310,4	1,031
	3	3	325	312,4	1,040
	4	4	295	314,3	0,939
2	1	5	310	316,2	0,980
	2	6	325	318,1	1,022
	3	7	340	320,1	1,062
	4	8	305	322,0	0,947
3	1	9	315	323,9	0,973
	2	10	335	325,8	1,028
	3	11	350	327,8	1,068
	4	12	310	329,7	0,940

Сначала следует оценить тренд. Для этого к данным табл. 4.5. подберем линейную модель тренда по методу наименьших квадратов.

(4.9.2)

Результаты расчетов трендовых значений для t=1,..,12 представлены в пятом столбце таблицы.

Произведем оценку сезонной составляющей модели как отношение фактического размера реализации к значению тренда. Результаты расчетов приведены в последнем столбце таблицы.

Полученные оценки сезонной компоненты пока еще не пригодны для построения прогнозов, поскольку они показывают сезонное отклонение от тренда для конкретного периода времени. Для того, чтобы оценки сезонности можно было использовать в целях получения прогноза, скорректированного с учетом сезонных изменений, необходимо найти средние оценки сезонной компоненты.

Рассчитаем средние индексы сезонности. Для первого квартала индекс сезонности равен

Для второго квартала

Для третьего квартала

Для четвертого квартала

Взаимная погашаемость сезонных воздействий в мультипликативной модели выражается в том, что сумма значений сезонной компоненты по отдельным периодам должна быть равна числу периодов в цикле. В нашем примере число периодов в цикле равно 4. Найдем сумму средних оценок сезонной компоненты

Полученные значения индексов сезонности не требуют корректировки и могут использоваться в моделях прогнозов.

Найдем прогноз на четвертый год . Для первого квартала (t=13) прогноз размера реализации равен

(306,6+1,9

Для второго квартала

(306,6+1,9

Для третьего квартала

(306,6+1,9

Для четвертого квартала

(306,6+1,9

10. ДИАГНОСТИЧЕСКАЯ ПРОВЕРКА АДЕКВАТНОСТИ МОДЕЛЕЙ. КРИТЕРИЙ ДАРБИНА-УОТСОНА.

Формально качество модели определяется ее адекватностью и точностью прогноза.

Модель считается адекватной, если ряд остатков удовлетворяет требованиям нулевого среднего, случайности, независимости последовательных значений и в ряде случаев нормальности.

Для проверки свойства нулевого среднего рассчитывается среднее значение остатков

.

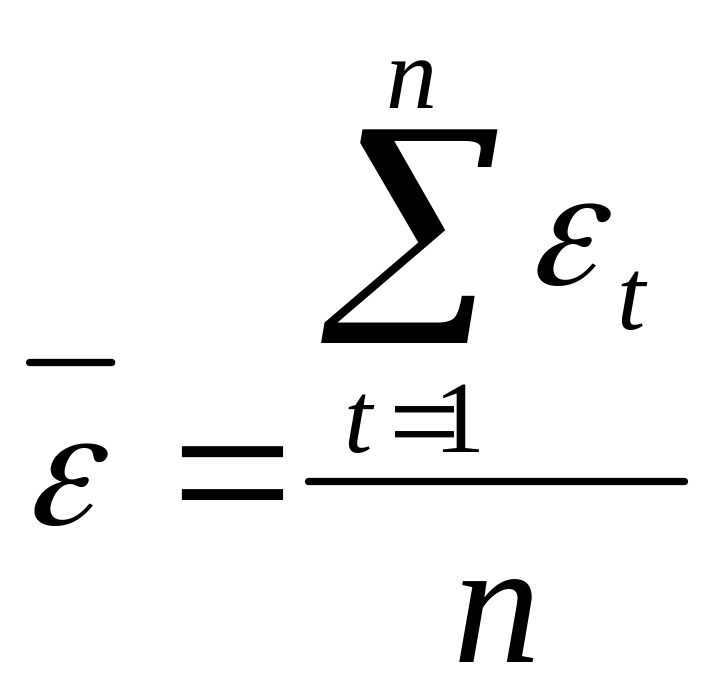Если близко к нулю, то можно считать, что модель не содержит систематической ошибки и адекватна по критерию нулевого среднего. Этот вопрос может быть решен со статистических позиций.

.

Гипотеза принимается, если

,

где

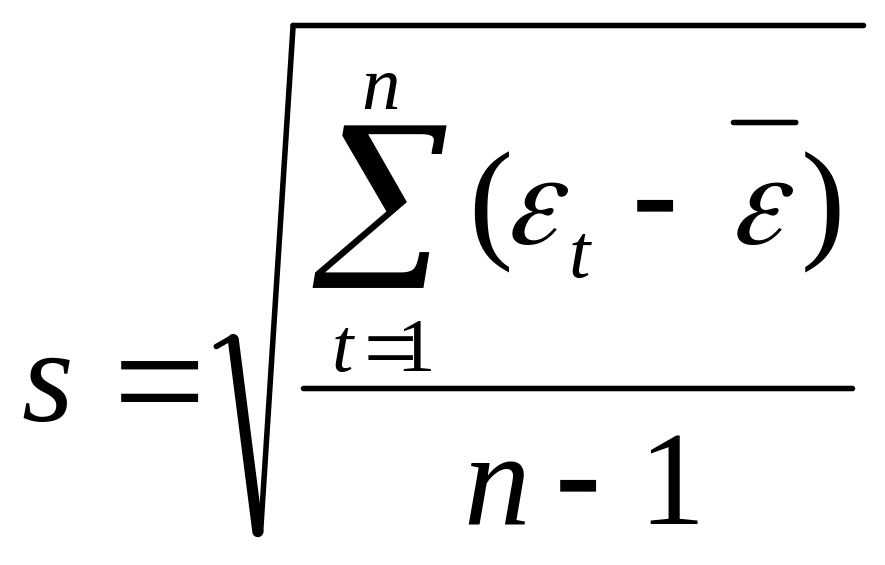- среднее квадратичное отклонение остатков;

- табличное значение критерия Стьюдента с n-1 степенью свободы уровня значимости .

Далее осуществляется проверка остаточного ряда по критерию случайности.

Проверка независимости последовательных остатков может осуществляться также по критерию Дарбина-Уотсона:

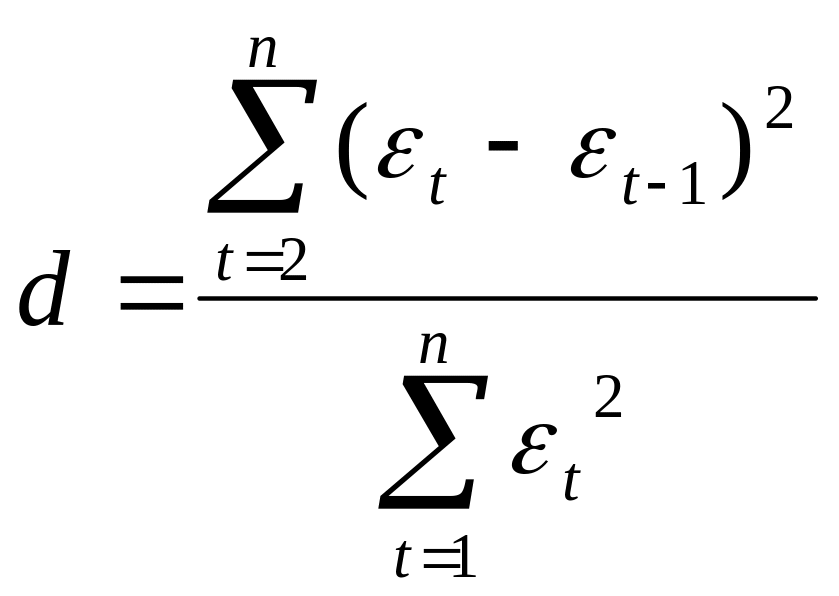. (4.10.1)

Несложные вычисления позволяют проверить, что статистика Дарбина- Уотсона следующим образом связана с выборочным коэффициентом корреляции между соседними наблюдениями.

(4.10.2)

В самом деле

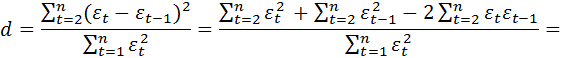
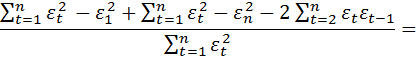
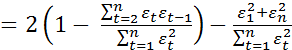
При большом числе наблюдений n сумма значительно меньше и

,

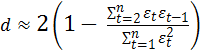откуда и следует приближенное равенство (4.10.2), так как в силу условия

Естественно, что в случае отсутствия автокорреляции выборочный коэффициент окажется не сильно отличающимся от нуля, а значение статистики d будет близко к двум.

Для рядов с тесной взаимосвязью между последовательными уровнями значение d близко к нулю; это свидетельствует о том, что регулярная составляющая не полностью отражена в модели тренда, т. е. модель не адекватна реальному процессу. Если последовательные остатки независимы, то d близко к 2, и это свидетельствует о хорошем качестве модели. При отрицательной автокорреляции остатков (строго периодическом чередовании их знаков) d близко к 4.

Заметим, что тест Дарбина-Уотсона, вообще говоря, не представляет собой статистический критерий в том смысле, что нельзя указать критическую область, которая позволяла бы отвергнуть гипотезу об отсутствии корреляции, если бы оказалось что в эту область попало наблюдаемое значение статистики d.

Тест работает следующим образом.

Если d , то значение d сравнивается с табличными значениями d_L и d_U:

- если , то гипотеза о независимости отвергается;

- если , то гипотеза о независимости принимается;

- если , то нет достаточных оснований для принятия решения.

Если , то с критическими значениями d_L и d_U, взятыми из таблиц, сравнивается не d, а 4- d и решение принимается по тем же правилам.

Изобразим результат Дарбина –Уотсона в виде таблицы

0<
Н0 отвергается (положительная автокорреляция)	Зона неопреде-ленности	Н0 принимается (отсутствие автокорреляции)	Зона неопреде-ленности	Н0 отвергается (отрицательная автокорреляция)

Совокупный критерий согласия Бокса-Пирса рассматривает совокупность первых k автокорреляций ряда остатков  ₁(), ₂(),…, _k():

Статистика Q имеет ²- распределение с k-m-1 степенями свободы. Пороговое значение для величины Q определяется по таблице.

Нормальность ряда остатков проверяется с целью использования этого свойства в дальнейшем при построении доверительных интервалов прогноза.

Ввиду малого числа наблюдений в большинстве временных рядов (меньше 30) это свойство может быть проверено лишь посредством вычисления оценок коэффициентов асимметрии и эксцесса для ряда остатков

; ,

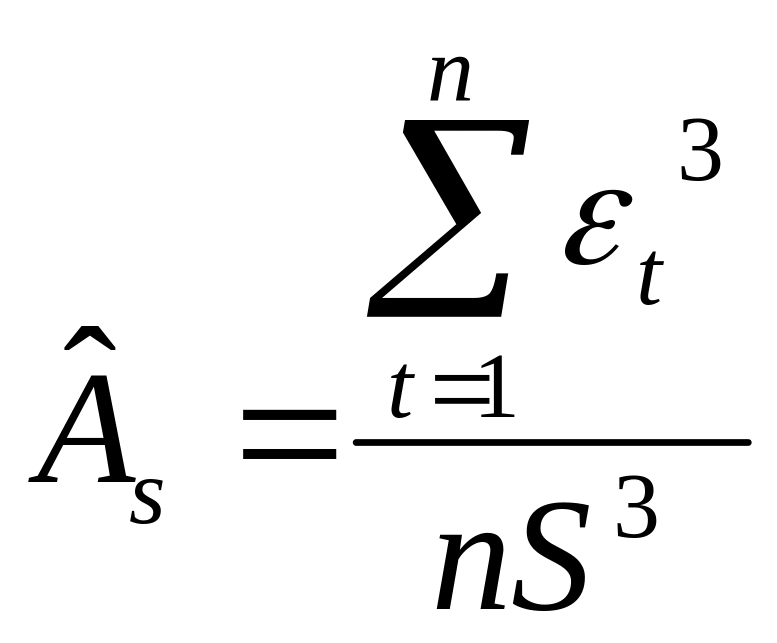где S – средняя квадратичная ошибка

.

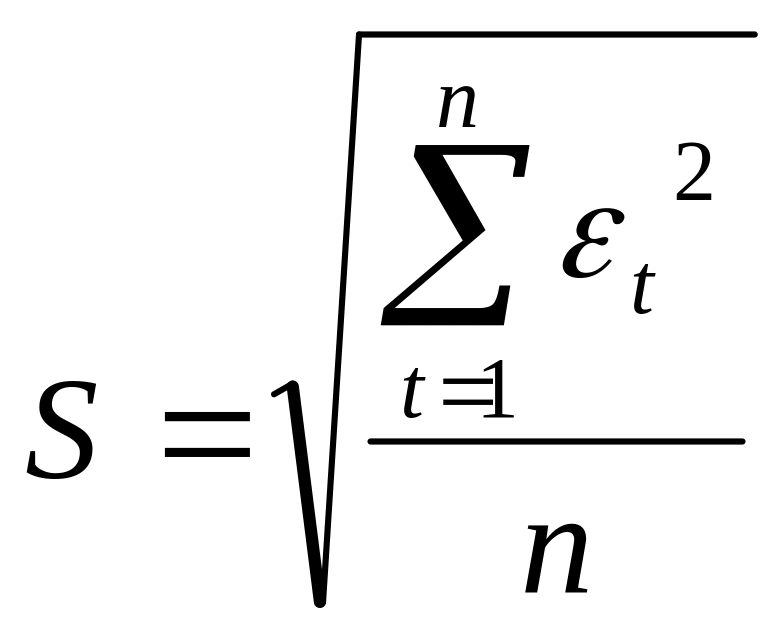Для нормального распределения и .

Гипотеза Н₀ о нормальном распределении ряда остатков ( ; ) принимается, если выполняются соотношения:

;

.

В этом случае доверительные интервалы для прогноза будут достаточно достоверными.

4.11. ОСНОВНЫЕ ПРОБЛЕМЫ ИДЕНТИФИКАЦИИ