13.Вопросы по теме»ряды и операционное исчисление решении Дифференциальных уравнений и систем

13.1Решение задачи Коши с помощью степенных рядов

Напомним формулировку теоремы Коши о существовании и единственности решения дифференциального уравнения первого порядка:

y^/=f (x) (27)

Если функция f (x, y) непрерывна в некоторой области D плоскости хоу и имеет там ограниченную производную  , то в каждой внутренней точке   существует функция  , и притом единственная, удовлетворяющая уравнению y^/=f (x) и условию y₀=y (x₀), т.е.   где 

Функция  , удовлетворяющая начальным условиям y₀=y(x₀), называется частным решением дифференциального уравнения первого порядка.

Рассмотрим два метода решения задачи о нахождении частного решения дифференциального уравнения с заданными начальными условиями.

Первый метод основан на последовательном дифференцировании исходного уравнения и применении ряда Тейлора:

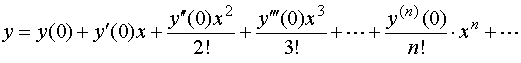
при условии, что х₀ = 0 и у₀ = у(0) или

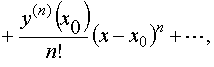
если х = х₀ и у₀ = у(х₀), причём полученное разложение как решение задачи Коши существует, и единственно.

Ищем коэффициенты ряда Тейлора: у(х₀) = у₀ по условию. Подставив у₀ в уравнение (27), найдём у^/(х₀) = f(х₀, у₀).

Следующий коэффициент ряда у^//(х₀) найдём, дифференцируя уравнение (27) как функцию двух переменных

 и т. д.

Пример 17. Решить уравнения. Найти первые пять членов разложения:

17.1. y^/=e^–x–y, y (0) = 0 17.2. y^/ = 2x cos x + y² , y(0) = 1.

Решение. Ищем решение задачи Коши в виде ряда

17.1. Коэффициент у(0) = 0 по условию. Подставляя начальные условия в дифференциальное уравнение, имеем

y ^/ (0) = e ⁰ – 0 = 1.

Дифференцируем уравнение и вычисляем последующие коэффициенты:

На этом остановимся, поскольку по условию необходимо найти только пять ненулевых членов ряда.

Итак, решение имеет вид

или

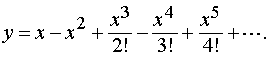
17.2.   где у(0) = 1 по условию;

Итак,

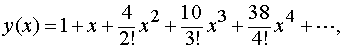
или

Второй метод, метод неопределённых коэффициентов, удобно использовать для решения линейных дифференциальных уравнений

 (10.28)

где функции с₁(х), с₂(х), …, с_п(х), f(x) разлагаются в ряды по степеням (х - х₀), сходящиеся в некотором интервале  .

Решение дифференциального уравнения (10.28) ищем в виде многочлена

(10.29)

где а₁, а₂, …, а_п - неопределённые коэффициенты.

Подставляем многочлен (10.29) и его производные в уравнение (10.28), затем приравниваем коэффициенты при одинаковых степенях х в левой и правой частях равенства. Остаётся решить полученную систему уравнений.

Пример 18. Решить уравнения. Найти первые шесть членов разложения:

18.1. y^/=y, y(0)=1;

18.2. y^///-2xy^//=e^-x, y(0)=-1, y(0)=-1, y^//(0)=2.

Решение

18.1. Ищем решение дифференциального уравнения в виде многочлена (10.29), дифференцируя который, получаем

y^/(x)=a₁+2a₂x+3a₃x²+4a₄x³+5a₅x⁴+…. (10.30)

Подставим у и уў в исходное уравнение

a₁+2a₂x+3a₃x²+4a₄x³+5a₅x⁴+…= a₀+a₁x+a₂x²+a₃x³+a₄x⁴+….

Приравниваем коэффициенты при одинаковых степенях х:

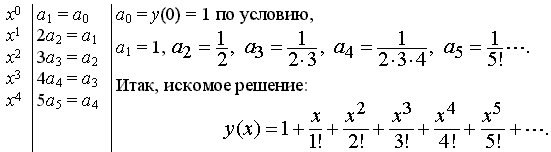
Заметим, что полученный ряд сходится к функции е^х (см. 10.21), которая и является частным решением данного дифференциального уравнения первого порядка.

Действительно, разделив переменные и проинтегрировав, получим общее решение данного уравнения:

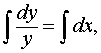    ln y=x+ln c,     y=ce^x.

Частное решение найдём, вычислив константу с. Подставим начальные условия в общее решение:

Отсюда частное решение у = е^х.