
- •1. Понятие эконометрики. Осн-е задачи эконометрики
- •2. Понятие корреляции и регрессии. Виды регр-й и корр-ий. Задачи регр-ого и корр-ого анализа.
- •4. Метод наимен квадратов (мнк)
- •5.Коэффициент корреляции.
- •7. Анализ точности определения оценок коэффициентов регрессии
- •8. Проверка гипотез относит. Коэф-тов лин. Ур-я регрессии
- •9. Интерв. Оценки коэф-ов лин. Ур-ния регрессии
- •10. Доверительный интервал для зависимой переменной
- •14. Дисперсии и станд. Ошибки коэф-в мр
- •17. Проверка общего кач-ва уравнения множественной регрессии.
- •19. Проверка равенства двух коэффициентов детерминации
- •26 Показательная модель.
- •31.Основные проблемы, возникающие при решении задач векторной оптимизации.
- •3. Проблема определения области компромисса.
- •32. Методы решения многоцелевых задач.
- •36. Метод равных и наименьших относительных отклонений.
14. Дисперсии и станд. Ошибки коэф-в мр
Знание дисперсии и станд. ошибок позвол-т анализ-ть точность оценок, строить доверит. интервалы для теоретич. коэф-в регр-ии, проверять соотв-щие гипотезы. Наиб. удобной ф-лой расчета данных хар-к явл-ся матрица.
1


………

0 0 … 1
D( 1)
1)
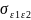 ...
...

 D(
2)
...
D(
2)
...
 .................................
.................................

 ...
D(
n)
...
D(
n)
1. М( )=0
2
 .
D(
)=
.
D(
)= 2
2 1
1
1
1
3. K( )= )= 2E, где = 2 , n*1= 1 ,En*n= , K( ) =
… ...
n 1
В
предыд. пункте была получена ф-ла опр-я
эмпирич. коэф-в множеств. линейн. регресии
: В=(
)-1
ХТУ.
Подставим в данную ф-лу теоретич. знач-я
зависим-й переменной: У= +
,
+
,
В=(
)-1 +
+ =(
)-1(
)
=(
)-1(
) +(
)-1
+(
)-1 =
+(
)-1
.
=
+(
)-1
.
Из последней ф-лы следует, что В- =( )-1 .
Построим дисперсионно-ковариационую матрицу вектора оценок параметра: K(В)=М((В-М(В))*(В-М(В))Т)=М((В- )*(В- )Т)=
=
М(((
)-1
)*((
)-1
)Т)=
М((
)-1 )-1).
)-1).
Т.к.
все независимые перем-ые
 ,
j=
,
j= не явл-ся случ. величинами, то получим:
не явл-ся случ. величинами, то получим:
Х(В)=(
)-1
 )-1=(
)-1
)-1=(
)-1
 2E
2E )-1=
2
)-1.
)-1=
2
)-1.
Получим,
что дисперсия оценок: D(bj)=
2zjj
,
j= ,
где zjj
– диагональный эл-т матрицы
)-1.
,
где zjj
– диагональный эл-т матрицы
)-1.
Но т.к. знач-е дисперсии 2 по выборке опр-ть невозможно, то оно замен-ся соотв-ей несмещенной оц-кой:
S2= /n-m-1.
Значит по выб-ке мы можем опр-ть лишь
выборочн. дисперсии эмпирич. коэф.
регрессии:
/n-m-1.
Значит по выб-ке мы можем опр-ть лишь
выборочн. дисперсии эмпирич. коэф.
регрессии:
S2(bj)=
S2
zjj=
/n-m-1)*
zjj
,
j=
.
Аналогично
как и в парной регр. S= – станд. ошибка регр.
– станд. ошибка регр.
S2(bj)= – стандартная ош-ка коэф. регр.
– стандартная ош-ка коэф. регр.
15.
После
опред-я точечных знач-й
 ,
j=
,
j= теор-х
коэф-ов регрессии мы можем опред-ть
интервальные оценки указан-х коэф-ов.Для
этого строит-ся t-статистика.
теор-х
коэф-ов регрессии мы можем опред-ть
интервальные оценки указан-х коэф-ов.Для
этого строит-ся t-статистика. -
- )/S(
),кот.
имеет распред-е Стьюдента с υ=n-m-1.По
выбранному уровню значим-ти(α) опред-м
)/S(
),кот.
имеет распред-е Стьюдента с υ=n-m-1.По
выбранному уровню значим-ти(α) опред-м
 ,
кот.
удов. соотнош-ю P(
,
кот.
удов. соотнош-ю P( )=1-α.
После преобраз-я для теор-х коэф-ов
регрессии получим доверительные
интервалы вида:
-
)=1-α.
После преобраз-я для теор-х коэф-ов
регрессии получим доверительные
интервалы вида:
- *
S(
)<
<
+
*
S(
),
где S(
)=
=
*
S(
)<
<
+
*
S(
),
где S(
)=
= =
=
 Аналогично
с парной регрессией можно постр-ть в
матрич. форме оценку для сред. знач-я
зависимой перемен.,когда X=
Аналогично
с парной регрессией можно постр-ть в
матрич. форме оценку для сред. знач-я
зависимой перемен.,когда X= ,
,
 -
*S*
-
*S* <M(
<M( /
)<
+
*S*
/
)<
+
*S*
16.Проверка
стат значимости коэф ур-ния регресс.
Как
и в случае парн регрес стат значимость
коэф множ лин регрес с m
объясняющими перемен проверяется на
основе t-стат:
 имеющей
в данной ситуации распределен Стьюдента
с числом степеней свободы ν=
n-m-1.
При требуемом уровне значимости
наблюд значение t-стат
сравнивается с крит точкой tα/2,n-m-1
распредел
Стьюдента.
имеющей
в данной ситуации распределен Стьюдента
с числом степеней свободы ν=
n-m-1.
При требуемом уровне значимости
наблюд значение t-стат
сравнивается с крит точкой tα/2,n-m-1
распредел
Стьюдента.
17. Проверка общего кач-ва уравнения множественной регрессии.
Для
этого используется коэф-т детерминации
 , 0≤R2≤1.
На ряду с коэф-том детерминации R2
использ-ся скорректированный (исправленный)
коэф-т детерминации, для этого в числителе
и знаменателе делается поправка на
число степеней свободы
, 0≤R2≤1.
На ряду с коэф-том детерминации R2
использ-ся скорректированный (исправленный)
коэф-т детерминации, для этого в числителе
и знаменателе делается поправка на
число степеней свободы
 ,
,
 ,
последнюю формулу легко получить, если
в формуле R2
разделить числитель и знаменатель на
,
последнюю формулу легко получить, если
в формуле R2
разделить числитель и знаменатель на
 ,
понятно, что
,
понятно, что
 .
Доказано, что добавление в модель новых
объясняющих переменных осущ-ся до тех
пор, пока растет скорректир-й коэф-т
детерминации. После проверки статистической
значимости каждого коэф-та регрессии
можно проверить совокупную значимость
коэф-тов, такой анализ осущ-ся на основе
проверки гипотезы об общей значимости,
т.е. гипотезы об одновременном равенстве
0 всех коэф-тов при объясняющих переменных:
Н0:
b1=b2=…=bn=0.
Если гипотеза Н0
не откланяется, то в этом случае совокуп-е
влияние всех объясняющих переменных
на зависимую переменную можно считать
статистич-ки несущественным, а общее
кач-во уравнения регрессии невысоким.
Данная гипотеза проверяется на основе
сравнения объясненной и остаточной
дисперсий. Н0:
объясненная дисперсия = остаточной
дисперсии; Н1:
объясненная дисперсия > остаточной
дисперсии. Для этого строится F-строка
по формуле:
.
Доказано, что добавление в модель новых
объясняющих переменных осущ-ся до тех
пор, пока растет скорректир-й коэф-т
детерминации. После проверки статистической
значимости каждого коэф-та регрессии
можно проверить совокупную значимость
коэф-тов, такой анализ осущ-ся на основе
проверки гипотезы об общей значимости,
т.е. гипотезы об одновременном равенстве
0 всех коэф-тов при объясняющих переменных:
Н0:
b1=b2=…=bn=0.
Если гипотеза Н0
не откланяется, то в этом случае совокуп-е
влияние всех объясняющих переменных
на зависимую переменную можно считать
статистич-ки несущественным, а общее
кач-во уравнения регрессии невысоким.
Данная гипотеза проверяется на основе
сравнения объясненной и остаточной
дисперсий. Н0:
объясненная дисперсия = остаточной
дисперсии; Н1:
объясненная дисперсия > остаточной
дисперсии. Для этого строится F-строка
по формуле:
 . F-статистика
имеет распредиление Фишера, которое
при выполнимости прелпосылок МНК имеет
следующее число степеней свободы: ν1=m,
ν2=n-m-1,
по заданному уровню значимости α и
числам ν1
и ν2
определяется F-критическое: Fкр=Fα,m,n-m-1.
Если F>Fкр,
то гипотеза Н0
откланяется в пользу Н1,
это значит, что объясненная дисперсия
> остаточной дисперсии, а это в свою
очередь значит, что построенное уравнение
регрессии хорошо описывает поведение
зависимой переменной.
. F-статистика
имеет распредиление Фишера, которое
при выполнимости прелпосылок МНК имеет
следующее число степеней свободы: ν1=m,
ν2=n-m-1,
по заданному уровню значимости α и
числам ν1
и ν2
определяется F-критическое: Fкр=Fα,m,n-m-1.
Если F>Fкр,
то гипотеза Н0
откланяется в пользу Н1,
это значит, что объясненная дисперсия
> остаточной дисперсии, а это в свою
очередь значит, что построенное уравнение
регрессии хорошо описывает поведение
зависимой переменной.
На
практике вместо указанной гипотезы
проверяется гипотеза о статистической
значимости коэф-та детерминации: Н0:
R2=0,
Н1:
R2≠0.
Для этого строится F-строка вида:
 .
.
18.
Анализ осущ на основе проверки гипотезы
об общей значим-ти- гип об одновр-м
равенстве нулю всех коэф-в регрессии
при объясняющих перем-х
 o:
o: =
= =…….
=……. =0.
Если
o
не отклоняется, то совок-е влияния всех
объясняющ перем-х на завис-ю перем-ю
можно счит-ь стат-и не существ-ым, а общее
кач-во урав-я регресс-и не высокое. Данная
гипотеза провер-ся на основе сравнения
объясненной и остаточ-й дисперсии.
o:
объяс-я дисперсия=остаточ-й,
ı:
объясн-я дисперсия > остаточ-я дисперс-я.
Для этого строи-ся F
статистика по формуле: F=
=0.
Если
o
не отклоняется, то совок-е влияния всех
объясняющ перем-х на завис-ю перем-ю
можно счит-ь стат-и не существ-ым, а общее
кач-во урав-я регресс-и не высокое. Данная
гипотеза провер-ся на основе сравнения
объясненной и остаточ-й дисперсии.
o:
объяс-я дисперсия=остаточ-й,
ı:
объясн-я дисперсия > остаточ-я дисперс-я.
Для этого строи-ся F
статистика по формуле: F=
 .
F
стат-ка имеет распред-ие Фишера, кот при
выполнимости пердпос-к МНК имеет
следующ-е число степеней свободы: υı=m,
υ₂=n-m-1.
По заданному уровню значим-ти λ и числам
υı, υ₂
опред-ся Fкритич=Fλ,m,n-m-1,если
F>Fкритич,
то гипотеза
o
отклон-ся в пользу
ı
это значит, что объяснен-я дисперсия
больше остаточной дисп-и, а это означ
что построенное уравн-ие регресс хорошо
описывает повед-ие зависим-й переем-й.
На практике вместе с указ-ой гипотезы
провер-ся гипотеза о стат. Значим. Коэф-та
детерминации:
o:
R²=0,
ı:R²
.
F
стат-ка имеет распред-ие Фишера, кот при
выполнимости пердпос-к МНК имеет
следующ-е число степеней свободы: υı=m,
υ₂=n-m-1.
По заданному уровню значим-ти λ и числам
υı, υ₂
опред-ся Fкритич=Fλ,m,n-m-1,если
F>Fкритич,
то гипотеза
o
отклон-ся в пользу
ı
это значит, что объяснен-я дисперсия
больше остаточной дисп-и, а это означ
что построенное уравн-ие регресс хорошо
описывает повед-ие зависим-й переем-й.
На практике вместе с указ-ой гипотезы
провер-ся гипотеза о стат. Значим. Коэф-та
детерминации:
o:
R²=0,
ı:R² F=
F= .
.
