26 Показательная модель.

П оказательная модель: Y = β₀е^{β1 Х}. Важным ее приложением является ситуация, когда анализируется изменение переменной Y постоянным темпом прироста во времени. В этом случае переменная Х символически заменяется переменной t: Y=β₀ . Данная функция путем логарифмирования (ln e^β1t = β₁t) сводится к лог –линейной модели: ln Y = ln β₀ + β₁t/

В общем случае Y =β₀ ,где -произвольная положительная константа, .

Данная функция к исходной вследствие тождества: .

Ряд экономических показателей моделируется через функции, являющиеся композицией перечисленных функции, что позволяет свести их к линейным. Например, производственная функция Кобба-Дугласса с учетом научно-технического прогресса: Y = . Прологарифмировать данную функцию, получим соотношение:

ln Y = ln A+αln K+βlnL+yt, которое сводится к линейному заменами ln Y =y, ln A=a, ln K = k, ln L= l.

27.Преобр-е случ.отклон-ий. Важн.значение имеет выпол-сть опред.предпосылок МНК для случ.отклонений.Они требуют,чтоб отклонения ε_i явл-сь нормально распред-ми случайн. величинами с нулевым мат. ожид-ем и постоян. дисперсией σ² и не коррелировали др. с другом (ε_i~N(0;σ²),cov(ε_i,εj)=0 при i≠j). При невыполнтмости указан. предпосылок оценки, получен. по МНК, не будут обладать св-ми BLUE-оценок, и проводимые для них тесты окаж-ся ненадежн. Если совокупн. Логарифмир-ние не треб-ся, с аддитив-м случайн. членом выполнимость предпосылок МНК имеет место, а следов-но, нет проблем с оцениваем. Для описания возможн.проблем со случ-м отклон-ем. воспользуемся моделью Y=A*X^B, дополнив ее случ-м членом. Случайный член ε может входить в соотнош-е в различн.видах. Рассмотрим 3 возможн. случая: Y=A*X^B*e^e (1);Y=A*X^B*e (2); Y=A*X^B+e (3).Данн. модели явл-ся нелин-ми относ-но параметра β. Прологарифмировав кажд.из этих соотнош-й, соответ-но получим: lnY=a+β*lnX+ε (4); lnY=a+β*lnX+lnε (5); lnY=ln(A+X^β+ε) (6). Здесь a=lnA. Использов-е(4)для оценки параметров в(1)не вызывает осложнений, связ-х со случ-м тклон-ем.Преобраз-е(2)в(5)приводит к преобр-ю случ. отклонений ε_i в lnε_i. Использ-ние МНК в(5)для нахождения BLUE- оценок параметров требует, чтобы отклон-я ν_i=lnε_i удовлетв-т предпос-ам МНК: ν_i~N(0, σ²). Но это возможно только в случае логарифм-ски нормальн.распред-я СВ ε_i c M(ε_i)=e^{(y^2)/2}иD(ε_i)=e^{y^2}(e^{y^2}-1). Логариф-кое соотнош-е(3) не привело к линеаризации соотнош-я относит-но парам-ов. Т.о. при исполь-нии преобраз-ний с целью нахожд-я оценок необходимо особ. вним-е уделять св-вам случайн.отклон-й, чтобы получен-е в результате оценки имели высок.статистич.значимость.

30. Постановка и математическая модель задачи векторной оптимизации. Многие экон.-управленческие задачи яв-ся многоцелевыми, напр., производственная программа предприятия д. обеспечить максим. возможный объем выпуска продукции, низкую ее себестоимость, высокие показатели рентабельности и др. В силу этого оптимальное решение по 1-му критерию м. оказаться не лучшим по другим критериям. Множество критериев м. представить в виде векторной целевой функции F(x)=(f1(x), f2(x),…, fK(x)). Для того, чтобы минимизировать частный критерий fK(x), достаточно максимизировать fk(x), т.к. min fk(x)=-max fk(x). Поэтому будем считать, что в дальнейшем каждая компонента векторного критерия максимизируется. Задача многоцелевой оптимизации записывается как векторная задача математического программирования:

max F(x) = (f1(x), f2(x),…, fK(x)) (1)

(2)

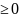xj , j= (3)

Будем рассматривать задачу 1-3 для случая, когда оптимальные решения , k= полученные при решении задачи по каждому решению не совпадают.

Найти решение, при котором значения всех критериев одновременно будет наилучшим, можно в области компромисса, кот. Находится в области допустимых решений. Решения, кот. Доставляют критериям наилучшие значения одновременно, называются эффективными, компромиссными, оптимальными по Паретто.

План Х1 не хуже плана Х2, если fk(Х1) fk(Х2), k= .

Если среди последних неравенств хотя бы 1 строгое, то план Х1 наз-ся предпочтительнее плана Х2. План Х1 оптимален по Паретто, если он допустим и не существует другого плана Х2, для кот. fk(Х1) fk(Х2) и хотя бы для 1 критерия выполняется строгое неравенство.