
- •16. Означення похідної фунуції. Основні теореми про похідні. Таблиця похідних.
- •17. Диференціювання неявної функції.
- •18. Правило Лопіталя.
- •19. Диференціал функції. Диференціал складної функції. Основні властивості диференціала.
- •21. Частковий та повний приріст, границя та неперервність функцій багатьох змінних.
- •Границя функції багатьох зміннихфункція формула неперервність змінна
- •22. Часткові похідні функцій декількох змінних.
1.Матрицы .Виды матриц
Матрицей называется множество чисел, образующих прямоугольную таблицу, которая содержит m строк и n столбцов.
Для любого элемента aij первый индекс i означает номер строки, а второй индекс j - номер столбца.
Если число строк матрицы не равно числу столбцов то матрица называется квадратная. Число строк или столбцов квадратной матрицы называется ее порядком.
Диагональ с лева на право - главная, а с право на лево - побочная.
Если только по главной диагонали матрицы стоят числа отличные от нуля, а все остальные элементы матрицы 0,то матрица называется диагональная.
Если у диагональной матрицы все числа главной диагонали равны, то матрица называется скалярной.
Если это 1 матрица называется единичной.
Матрица в которой все элементы равны 0, то матрица называется нулевой.
Бывают матрицы строки и матрицы столбцы - они называются векторами.
Если у матриц одинаковое число строк и столбцов и их соответствующие элементы равны то матрицы равны.
Если переставить строки со столбцами - то матрица будет транспортированная.
2.Линейные операции над матрицами
Суммой матриц А и В условимся называть такую матрицу, элементы которой равны сумме соответствующих элементов матриц А и В. Складывать можно только матрицы, имеющие одинаковое строение.
Для любой матрицы А существует матрицы -А, такая что А+(-А)=0.
Произведением матрицы А на число к называется такая матрицы кА, каждый элемент которой равен кij
Умножение матрицы на число сводится к умножению на это число всех элементов матрицы.
Что бы найти элемент с11 первой строки и первого столбца матрицы С, нужно каждый элемент первой строки матрицы А умножить на соответствующий элемент первого столбца матрицы В и полученное произведение сложить
Для прямоугольных матриц справедливы следующие правила:
1)умножение матрицы А на матрицу В имеет смысл только в том случае, когда число столбцов матрицы А равно числу строк матрицы В;
2) в результате умножения двух прямоугольных матриц получается матрица, содержащая столько строк, сколько строк сколько в первой матрице, и столько столбцов, сколько во второй матрице
АВ не равно ВА, произведение двух матриц не подчиняется переместительному закону
Произведение двух ненулевых матриц может равняться 0
3.Определители та их свойства
Определителем второго порядка, называется число а11а22 - а12а21
Равен разнице главной и побочной диагонали
Определителем третьего порядка , называется число а11а22а33+а12а23а31+а21а32а13-а13а22а31-а12а21а33-а23а32а11
Свойства:
1. Определитель не изменится, если его строки поменять местами с соответствующими столбцами - свойство равноправности строк и столбцов;
2. При перестановки двух строк (или столбцов) определитель изменит свой знак на противоположный;
3. Общий множитель всех элементов строки (или столбца) можно вынести за знак определителя;
4. Определитель с двумя одинаковыми строками или столбцами равен нулю;
5. Если все элементы двух строк (столбцов) определителя пропорциональны, то определитель равен нулю;
6. Если к какой-либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число, то определитель не изменит своей величины;
7. Треугольный определитель, у которого все элементы, лежащие выше(или ниже) главной диагонали, - нули, равен произведению элементов главной диагонали;
4. Методы вычисления определителей. Миноры и алгебраические дополнения элементов определителя
Минором Мij элемента аij определителя D=|aij| , где i и j меняются от 1 до n , называется такой новый определитель, который получается из данного определителя путём вычеркивания строки и столбца, содержащих данный элемент
Алгебраическим дополнением элемента aij определите Д называется минор Мij этого элемента, взятый со знаком (-1)i+j
Принято обозначать Аij = (-1)i+jMij
Сумма произведений элементов любой строки (или столбца) определителя Д на их алгебраические дополнения равна этому определителю
Методы вычисления определителей:
1. Определитель можно вычислить, используя непосредственное его определение. Этим способом удобно находить определители второго и третьего порядков, а для определителя более высокого порядка применим следующий способ;
2. Определитель можно вычислить с помощью его разложения по элементам строки или столбца;
3 Определитель можно вычислить способом приведения к треугольному виду. Этот способ основан на том, что в силу свойства 7 треугольный определитель равен произведению элементов главной диагонали
Что бы получить треугольный определитель, нужно, используя свойство 6, к какой-либо строке (или столбцу) заданного определителя прибавлять соответствующие элементы другой строки (или столбца), умноженные на одно и то же число, до тех пор пока не придем к определителю треугольного вида;
Понятие обратной матрицы и ее вычисление. Теорема существования обратной матрицы
Квадратная матрица A называется вырожденной, если ее определитель равен нулю, и невырожденной, если ее определитель не равен нулю.
Если A - квадратная матрица, то обратной по отношению к А называется матрица, которая, будучи умножена на А(как справа, так и слева), дает единичную матрицу
А-1А =А А-1=Е
Если обратная матрица А-1 существует, то матрица А называется обратимой. Операция вычисления обратной матрицы при условии, что она существует, называется обращением матрицы.
Для того чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы матрица А была невырожденной.
Нахождение обратной матрицы:
1)Находим определитель матрицы А;
2)Находим алгебраические дополнения всех элементов и записуем в новую матрицу;
3)Меняем местами столбцы полученной матрицы;
4)Умножаем полученную матрицу на 1/Д
6. Решение систем линейных уравнений с помощью обратной матрицы
Нужно:
1) Найти обратную матрицу А-1;
2) Найти произведение обратной матрицы А-1 на матрицу-столбец свободных членов В 3) Пользуясь определением равных матриц, записать ответ
Для решения линейных уравнений нужно записать уравнение в матричной форме АХ=В
Метод Крамера для решения систем линейных уравнений
Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера (1704–1752), придумавшего метод.
Пример:

Определители:
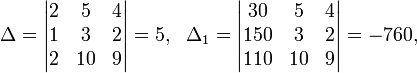
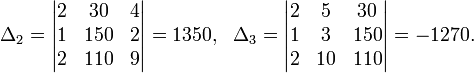
![]()
8. Метод Гаусса для решения систем линейных уравнений
Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Покажем, как методом Гаусса можно решить следующую систему:
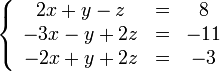
Обнулим
коэффициенты при ![]() во
второй и третьей строчках. Для этого
вычтем из них первую строчку, умноженную
на
во
второй и третьей строчках. Для этого
вычтем из них первую строчку, умноженную
на ![]() и
и ![]() ,
соответственно:
,
соответственно:
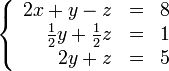
Теперь
обнулим коэффициент при ![]() в
третьей строке, вычтя из неё вторую
строку, умноженную на
в
третьей строке, вычтя из неё вторую
строку, умноженную на ![]() :
:

В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.
На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:
![]() из
третьего;
из
третьего;
![]() из
второго, подставив полученное
из
второго, подставив полученное ![]()
![]() из
первого, подставив полученные
и
.
из
первого, подставив полученные
и
.
9. Уравнение линии на плоскости. Виды уравнения прямой
Любое уравнение первой степени относительно неизвестных х и у является уравнением прямой на плоскости: АX + ВY + С = 0
Оно может быть записано в некоторых специальных видах:
а) уравнение с угловым коэффициентом у= kx+b , где k - угловой коэффициент, численно равный тангенсу угла наклона прямой к положительному направлению оси Ох , а свободный член b - ордината точки пересечения графика и Оу.
![]() -отрезок,
отсекаемый графиком на оси оу
-отрезок,
отсекаемый графиком на оси оу
Общее уравнение прямой на плоскости - рассмотрим на плоскости Оху произвольную прямую L. Пусть дана некоторая ее точка М1(х1у1) и вектор N=Ai+Bj, перпендикулярный рассматриваемой прямой. Этот вектор называется нормальным вектором прямой. Точка М1 и нормальный вектор N вполне определяют положение прямой L на плоскости Оху.
Каноническое уравнение - положение прямой L на плоскости вполне определяется заданием какой-либо ее точки М(х1,у1) и вектора S=mi+nj , параллельного L или лежащего на ней. Этот вектор называется направляющим вектором прямой L.
Уравнение прямой, проходящей через заданную точку в заданном направлении. Тогда каноническое уравнение прямой будет иметь вид:
|
получим у-у1 = k(х – х1) – это прежнее уравнение прямой с угловым коэффициентом. |
Уравнение прямой, проходящей через две данные точки. Пусть на плоскости даны М1(х1у1) и М2(х2у2). Составим каноническое уравнение прямой, проходящей через эти две точки в качестве направляющего вектора S возьмем M1M2 |
|
Уравнение прямой в отрезках х/а+у/в=1
Уравнением прямой в отрезках удобно пользоваться для построения прямой. Поэтому при необходимости уравнение прямой приводят к виду уравнения в отрезках и строят прямую
Окружность
Окружностью называется множество всех точек плоскости, равноудаленных от одной точки, называемой центром.
|OM| =
![]()
(x-a)^2+(y-b)^2=r^2 - Каноническое уравнение окружности с центром О(а;б) и радиусом r
Эллипс
Эллипсом называется множество точек на плоскости, сумма расстояний от каждой из которых до двух заданных точек(называемых фокусами) есть величина постоянная, большая, чем расстояние между фокусами.
Фокусы эллипса принято обозначать буквами F1 и F2, расстояние между фокусами - через 2c, сумму расстояний от любой точки эллипса до фокусов - через 2а(2а>2c).
Каноническое уравнение эллипса имеет вид:
х^2/а^2+у^2/б^2=1
a^2-b^2=c^2
Эксцентриситет эллипса - отношение расстояний между фокусами к длине большой оси = 2с/2а или 2с/2б
Если эксцентриситет равен нулю, то эллипс вырождается в окружность
12. Гипербола
Гиперболой называется множество точек плоскости, разность расстояний от каждой из которых до двух заданных точек(называется фокусами) есть величина постоянная. Эта постоянная величина положительна и меньше расстояния между фокусами
Каноническое уравнение гиперболы:
x^2/a^2-y^2/b^2 =1 или y^2/b^2-x^2/a^2=1
Эксцентриситетом гиперболы называется отношение расстояния между фокусами к длине действительной оси = 2с/2а или 2с/2б
2а>2c E>1
Прямые l1 и l2 называются асимптотами; их уравнения имеют вид
у=+-б/ах
13. Парабола
Параболой называется множество точек на плоскости, равноудаленных от заданной точки (называемой фокусом) и данной прямой(называемой директрисой).
Фокус параболы принято обозначать буквой F, директрису - буквой d, расстояние от фокуса до директрисы - буквой p (p>0).
Каноническое уравнение параболы, фокус которой расположен на оси абсцисс
y^2=2px или y^2=-2px
Каноническое уравнение параболы,фокус которой расположен на оси ординат
x^2=2py или x^2=-2py
14.Понятие предела функции. Основные теоремы про пределы. Первая и вторая определенная граница
Пусть величина х в процессе своего изменения неограниченно приближается к числу 5:4,9;4,99;4,999; или 5,1;5,01;5,001 Число 5 называется пределом переменной величины х.
Постоянная величина а называется пределом переменной х, если модуль разности |x-a| при изменении х становится и остается меньше любого как угодно малого положительного числа е.
Свойства:
1) Предел алгебраической суммы конечного числа переменных величин равен алгебраической сумме пределом слагаемых;
2)Предел произведения конечного числа переменных величин равен произведению их пределов;
3)Постоянный множитель можно выносить за знак предела;
4)Предел отношения двух переменных величин равен отношению пределов, если предел знаменателя не равен нулю;
5)Предел целой положительной степени переменной величины равен той же степени предела этой же переменной;
6)Если переменные x, y, z удовлетворяют неравенствам х<=y<=z и z->a, то y->a.
Число б называется пределом функции f(x) в точке а, если для всех значений x, достаточно близких к a и отличных от a, значения функции f(x) сколь угодно мало отличается от числа б.
15. Непрерывность функции. Свойства функции непрерывной в точке и на промежутке
Функция f(x) называется непрерывной в точке х=х0,если:
1) эта функция определена в точке х=х0 (т.е. определенному значению аргумента х, равному х0, соответствует вполне определенное значение функции y,равное y0;
2) приращение функции в точке х0, стремится к нулю
Функция f(x) называется непрерывной в данной точке х0, если ее предел в точке хо, существует и равен значению функции в этой точке
Свойства:
Если функция f1(x) и f2(x) непрерывны в точке a,то:
1)их сумма, разность, произведение является функциями, непрерывными в этой точке;
2) частное f1(x)/f2(x) есть непрерывная функция при условии f2(a) не равно 0.
Функция f(x) называется непрерывной на отрезке a,b, если она непрерывна в каждой точке этого отрезка
16. Означення похідної фунуції. Основні теореми про похідні. Таблиця похідних.
Похідна́ — основне поняття диференційного числення, що характеризує швидкість зміни функції. Визначається як границя відношення приросту функції до приросту її аргументу коли приріст аргументу прямує до нуля (якщо така границя існує). Функцію, що має скінченну похідну, називають диференційовною.
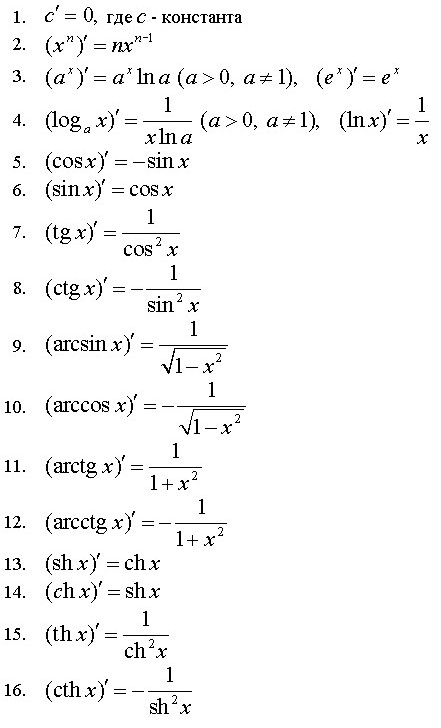
17. Диференціювання неявної функції.
Функція
![]() називається
неявною,
якщо вона задається рівнянням
називається
неявною,
якщо вона задається рівнянням
![]()
нерозв’язним
щодо
![]() .
Знайдемо частинні похідні
.
Знайдемо частинні похідні
![]() і
і
![]() неявної функції
,
заданої рівнянням (2.11). Для цього,
підставивши
в рівняння замість
функцію
неявної функції
,
заданої рівнянням (2.11). Для цього,
підставивши
в рівняння замість
функцію
![]() ,
отримаємо тотожність
,
отримаємо тотожність
![]() Частинні похідні по
Частинні похідні по
![]() і по
і по
![]() функції, тотожно рівній нулю, також
рівні нулю:
функції, тотожно рівній нулю, також
рівні нулю:
![]() (
– вважаємо сталою)
(
– вважаємо сталою)
![]() (
–
вважаємо сталою)
(
–
вважаємо сталою)
звідки
![]() і
і
![]()
Зауваження.
а)
Рівняння вигляду
не
завжди визначає одну змінну як неявну
функцію двох інших. Так, рівняння
![]() визначає функції
визначає функції
![]() або
або
![]() ,
визначені в крузі
,
визначені в крузі
![]() ,
,
![]() визначену
в півколі
при
визначену
в півколі
при
![]() і т. д., а рівняння
і т. д., а рівняння
![]() не визначає ніякої функції.
не визначає ніякої функції.
Має місце теорема існування неявної функції двох змінних:
Якщо
функція
![]() і її похідні
і її похідні
![]()
![]() визначені
і безперервні в деякій околі точки
визначені
і безперервні в деякій околі точки
![]() ,
причому
,
причому
![]() ,
a
,
a
![]() ,
то існує
окіл
точки
,
то існує
окіл
точки
![]() ,
в якій рівняння (2.11) визначає єдину
функцію
,
неперервну
і диференційовану в околі точки
,
в якій рівняння (2.11) визначає єдину
функцію
,
неперервну
і диференційовану в околі точки
![]() і таку, що
і таку, що
![]() .
.
б)
Неявна функція
![]() однієї
змінної задається рівнянням
однієї
змінної задається рівнянням
![]() .
Можна показати, що у випадку, якщо
виконуються умови
існування
неявної функції однієї змінної (є
теорема, аналогічна вищезгаданій), то
похідна неявної функції знаходиться
по формулі
.
Можна показати, що у випадку, якщо
виконуються умови
існування
неявної функції однієї змінної (є
теорема, аналогічна вищезгаданій), то
похідна неявної функції знаходиться
по формулі
![]()
![]()
18. Правило Лопіталя.
Правило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность
типа или .
Пусть a является некоторым конечным действительным числом или равно бесконечности.
Если
 и
и
 , то
, то
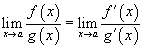 .
.Если
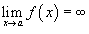 и
и
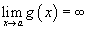 ,
то аналогично
.
,
то аналогично
.
Правило
Лопиталя можно также применять к
неопределенностям типа
![]() Первые
две неопределенности
Первые
две неопределенности
![]() можно
свести к типу
можно
свести к типу
![]() или
или
![]() с
помощью алгебраических преобразований.
А неопределенности
с
помощью алгебраических преобразований.
А неопределенности
![]() сводятся
к типу
сводятся
к типу
![]() с
помощью соотношения
с
помощью соотношения
![]() Правило
Лопиталя справедливо также и для
односторонних пределов.
Правило
Лопиталя справедливо также и для
односторонних пределов.
19. Диференціал функції. Диференціал складної функції. Основні властивості диференціала.
Диференціалом dy називають також диференціал першого порядку. З виразу (4) бачимо що диференціал функції є функція двох незалежних змінних х і х. Якщо y = х, то у' = х' =1, тому dy = dxx. Тобто диференціал незалежної змінної ототожнюється з її приростом, тобто диференціал незалежної змінної дорівнює приросту незалежної змінної
На цій підставі для будь-якої диференційованої функції y = f (x) можемо записати так: dy = f' (x) dx (5).
Ланцюгове правило (правило диференціювання складної функції) дозволяє обчислити похідну композиції двох і більше функцій на основі індивідуальних похідних.
Якщо
функція f має похідну в точці![]() , а функція g має похідну в точці
, а функція g має похідну в точці![]() , тоді складна функція h(x) = g(f(x)) також
має похідну в точці .
, тоді складна функція h(x) = g(f(x)) також
має похідну в точці .
Властивості диференціала.
Властивість 1. Диференціал суми дорівнює сумі диференціалів.
d (a + b) = da + db
Дана властивість застосовується незалежно від того, яка функція дана — тригонометрична або звичайна.
Властивість 2. Постійний множник можна винести за знак диференціала.
d (2a) = 2d (a)
Властивість 3. Твір складної диференційної функції дорівнює добутку однієї простої функції на диференціал другий, складеному з твором другої функції на диференціал першої. Виглядає це таким чином:
d (uv) = du * v + dv * u
Таким прикладом може служити функція y = x sinx, диференціал якої дорівнює:
y ‘= (xsinx)’ = (x) ‘* sinx + (sinx)’ * x = sinx + cosx ^ 2.
. Означення функції багатьох змінних. Геометрична інтерпретація.

 -
это уравнение прямой, проходящей
через две данные точки (х1 у1)
и (х2,
у2)
-
это уравнение прямой, проходящей
через две данные точки (х1 у1)
и (х2,
у2)