35.Диф.Рівняння 1-го порядку з відокремленими змінними.

1. Диференціальні рівняння і порядку

Диференціальне рівняння першого порядку в загальному випадку має вигляд F(x,y,y’) = 0. Якщо його можна розв'язати відносно y’, то воно набуває вигляду

y’ = f(x,y).

Співвідношення типу y’ = f(x,y) називається диференціаль­ним рівнянням першого порядку, розв'язаним відносно по­хідної у'.

Кажуть, що одне диференціальне рівняння рівносиль­не якомусь іншому, якщо множини розв'язків цих рів­нянь однакові.

Оскільки 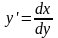, диференціальному рівнян­ню y’ = f(x,y) рівносильне рівняння в диференціальній формі dy = f(x,y)dx, в якому шуканою функцією вважається у.

Справедливою є така теорема про існування та єдиність розв'язку диференціального рівняння.

Теорема (теорема Коші). Якщо функція f(x,y) та її частинна похідна y’ = 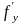(x,y) визначені й неперервні в деякій області 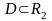i (a,b) - довільна фіксована точка області D, то існує єдина функція y(x), визначена та диференційована в деякому околі точки а, яка є розв'язком диференціального рівняння, що задовольняє умову y(a) = b.

Геометрично теорема означає, що для кожної точ­ки (a,b) області D снує єдиний розв'язок y(x) диференці­ального рівняння y’ = f(x,y), графік якого (мається на увазі графік функції y(x) проходить через точку (a,b))

Із цієї теореми випливає, що диференціальне рівняння y’ = f(x,y) має нескінченну кількість розв'язків (наприклад, розв'язки, графіки яких проходять через точку (a,b), точ­ку (a, b₁) і т. д., якщо тільки ці точки є точками області D). Кожна функція множини {y = x² + c, c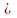 R} є розв'язком рівняння y’ = 2x.

Задача відшукання розв'язку диференціального рів­няння, що задовольняє умову y(a) = b, називається за­дачею Коші, а умова y(a) = b — початковою.

Означення. Функція y(x,c), де c — довільна стала, називається загальним розв'язком диференціального рів­няння y’ = f(x,y), якщо:

1) при будь-якому конкретному значенні сталої с вона є розв'язком цього рівняння;

2) для будь-якої початкової умови y(a) = b такої, що (a,b) — точка області D, сталу с можна пі­дібрати так, що функція y(x,c) задовольнятиме цю почат­кову умову.

Означення. Будь-яка функція, яка утворюється із загального розв'язку диференціального рівняння y’ = f(x,y) при конкретному значенні сталої с, називається частин­ним розв'язком цього рівняння.

Іноді у процесі відшукання загального розв'язку дифе­ренціального рівняння приходять до співвідношення Ф(х, у, с) = 0, яке не можна розв'язати відносно у. У цьому разі цю рівність називають загальним інтегралом диференціально­го рівняння. Якщо у співвідношенні сталій с надати конкретного значення, то дістанемо частинний ін­теграл диференціального рівняння.

Проінтегрувати або, як часто кажуть, розв'язати ди­ференціальне рівняння y’ = f(x,y), означає знайти його загаль­ний розв'язок чи загальний інтеграл (якщо початкову умову не задано) або відшукати той частинний розв'язок чи частинний інтеграл рівняння, який задовольняє задану початкову умову (якщо така є).

2. Диференціальні рівняння з відокремленими змінними.

Диференці­альне рівняння типу y’ = g(x)h(y) називається рівнянням з відокремлюваними змінними.

Для даного диференціального рівняння рівносильним є рівняння в диференціальній формі dy = g(x)h(y)dx, в якому шуканою є функція у.

Припускаючи, що h(y) ≠ 0 для всіх у з області визна­чення функції h(y). Знаходимо .

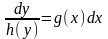Диференціальне рівняння називається рівнян­ням з відокремленими змінними (в ньому множник при dy є функцією, залежною тільки від y, а множник при dх є функцією, залежною тільки від x), а перехід від диферен­ціального рівняння y’ = g(x)h(y) до диференціального рівняння — відокремленням змінних у рівнянні y’ = g(x)h(y).

Обидві частини диференціального рівняння є ди­ференціалами функцій змінної x, або y = y(x). Оскільки диференціали рівні між собою

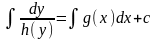
де під інтегралами розуміють деякі відповідні первісні (вважаємо, що вони існують), а с — довільна стала.

Отже, будь-який розв'язок у диференціального рів­няння міститься у співвідношенні .

Якщо це співвідношення містить усі розв'язки дифе­ренціального рівняння y’ = g(x)h(y), то воно є загальним інтегра­лом цього рівняння.

При відокремленні змінних можна втратити деякі розв'язки диференціального рівняння. Нехай, наприклад, y = b — розв'язок рівняння h(y) = 0. Оскільки h(b) =0 і db = 0, підставивши y = b в диференціальне рівняння dy = g(x)h(y)dx, рівносильне диференціальному рівнянню y’ = g(x)h(y), діс­танемо тотожність. Отже, при будь-якому x маємо y = b — розв'язок диференціального рівняння y’ = g(x)h(y). І якщо цей розв'язок не можна знайти із співвідношення при деякому значенні довільної сталої с, то його треба розгля­дати окремо від розв'язків, що містяться у цьому співвідношен­ні.

Іноді первісні, які входять у рівність , не є еле­ментарними функціями. Проте і тоді задачу інтегрування диференціального рівняння вважають розв'язаною і ка­жуть, що розв'язок диференціального рівняння виражено у квадратурах.

Це пов'язано з іншою назвою операції знаходження ін­тегралів — квадратурою, яку, зокрема, вживають у теорії диференціальних рівнянь.

36.Лінійне програмування