5.5. Связь кодового расстояния с корректирующей способностью кода.

Говорят, что код исправляет все – кратные ошибки, если декодирование по правилу минимума расстояния любого кодового слова с(и менее) ошибочными символами завершается правильным решением. Параметром, определяющим исправляющую способность кода, служит егокодовое расстояние.

Кодовым расстоянием кода называется минимальное расстояние Хэмминга между любой парой несовпадающих векторов кода

.

Теорема 5.5.1. Код исправляет любые ошибки кратности и менее в том и только в том случае, если кодовое расстояние удовлетворяет неравенству

. (5.5)

Доказательство:

Пусть имеется код с кодовым расстоянием. Предположим, что произошла ошибка кратности, и что найдутся два кодовых вектораитакие, что

,

а значит, не позволяющие исправить ошибку кратности . Однако, как следует из аксиом расстояния,

,

что противоречит условию теоремы. Следовательно, неравенство (5.5) определяет достаточное условие исправление ошибок кратности и менее.

С другой стороны, если , то обязательно возникнет ситуация, при которой произойдет неверное декодирование. Например, если, то существует такой вектор наблюдения, для которого, и, следовательно, наблюдается неопределенность в принятии решения. Таким образом, условие (5.5) является необходимым.

Полезной иллюстрацией приведенного доказательства может служить диаграмма, представленная на рис. 5.3. На ней изображены сферы Хэмминга радиуса c центром , представляющие собой множество точек (векторов), расположенных отна расстоянии Хэммингаили ближе. Если все сферы Хэмминга радиуса, окружающие кодовые вектора, не перекрываются, декодер воспримет любой вектор внутриi–ой сферы, как i–ый кодовый вектор . Это означает, что любая ошибка кратностии менее в кодовом слове будет исправлена. Вместе с тем, при условии исправления любых ошибок кратностиизбежать перекрытия сфер можно только в том случае, если минимальное расстояние Хэмминга между кодовыми векторами не меньше, чем.

Из представленной диаграммы легко увидеть, что обнаружение ошибок кратности в принятых векторах возможно тогда, когда выполняется условие

.

Из рассмотренного видно, что основными параметрами блокового кода являются: кодовое расстояние , его объеми длина. Часто при описании характеристик кода вместо объемаиспользуют либо число информационных символов в кодовом слове, либо скорость кода. Именно с этими параметрами связаны два основных варианта задач, рассматриваемых теорией кодирования. Первая из них связана с максимизациейпри заданных значениях(или) идля достижения хорошей корректирующей способности кода. Дуальной задачей является максимизация(или) при минимумеи длины.

5.6. Важнейшие границы теории кодирования.

Значительная часть всех работ по теории кодирования посвящена установлению и исследованию различных границ для кодов и, в частности, границ для кодового расстояния. Указанные границы представляют собой ориентиры, позволяющие объективно судить, насколько успешно решены задачи построения кодов, упомянутые в предыдущем параграфе.

Наиболее важными и полезными границами кодового расстояния являются границы Хэмминга, Плоткина и Гильберта. Первые две из упомянутых границ указывают предел максимизации кодового расстояния при заданных длине и скоростикода. Граница же Гильберта является границей существования и дает нижнюю оценку кодового расстояния «наилучшего» кода. Остановимся только на первой границе.

Теорема 5.6.1. (Граница Хэмминга). Для любого двоичного кода, содержащего кодовых слов длиныи исправляющего(и менее) ошибок, выполняется соотношение

, (5.6)

где – биномиальный коэффициент.

Иным вариантом представления границы может служить соотношение

,

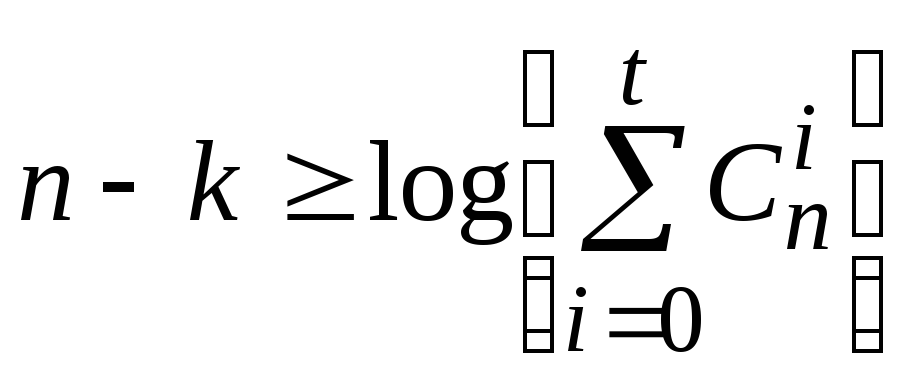устанавливающее минимально число проверочных символов, необходимое для обеспечения требуемой корректирующей способности.

Доказательство. Посчитаем «объем» сферы радиуса , изображенной на рис. 5.3, т.е. определим число точек, находящихся внутри сферы,

.

Требование однозначного декодирования означает, что сферы не должны пересекаться, и значит, общий объем, создаваемый всеми сферами, будет . Поскольку при длине кодового слова всего может существоватьвекторов наблюдения, то , что и завершает доказательство.

Замечание. В случае рассмотрения недвоичных, –ичных кодов, граница Хэмминга имеет вид

.

Коды, для которых достигается равенство в границе Хэмминга, называются совершенными.

Совершенные коды исправляют любую ошибку кратности и менее, но не исправляют ни одной ошибки большей кратности. Геометрически эти коды воплощают т.н. «плотную упаковку», когда вседвоичных векторов охваченысферами радиусабез пересечения и свободного пространства. В этой связи совершенные коды также называют плотно упакованными или сферически упакованными. Их совершенство заключается в достижении максимально возможной скоростипри фиксированныхи. Среди двоичных кодов известны три класса совершенных кодов – тривиальный код с повторением нечетной длины, коды Хэмминга, исправляющие любую однократную ошибку, и код Голея длины 23 и кодовым расстоянием 7 (исправляет любую 3–кратную ошибку и менее).

Пример 5.6.1. Убедимся, что для кодов Хэмминга действительно достигается равенство в (5.6). Коды Хэмминга характеризуются следующими параметрами:

.

Тогда из (5.6) следует

.

Фактические параметры кодов Хэмминга представимы следующим рядом – (3,1), (7,4), (15,11), (31,26), (63,57)…., где применено стандартная запись обозначения кода – первая цифра отвечает длине кодового слова , а вторая – числуинформационных символов в кодовом слове.

Коды, исправляющие любые ошибки кратности до включительно, а также некоторые ошибки кратности, и не исправляющие никаких ошибок большей кратности, называютсяквазисовершенными кодами.

Примером квазисовершенного кода может служить расширенный код Хэмминга с параметрами , получаемого из совершенного кода Хэмминга добавлением еще одного проверочного символа путем простой проверки на четность.

46