
- •Учебно-методическое пособие для выполнения индивидуального задания определенный интеграл
- •Предисловие
- •Понятие определенного интеграла. Вычисление определенных интегралов
- •1. Понятие определенного интеграла
- •2. Условия интегрируемости функций
- •4. Свойства определенного интеграла
- •5. Вычисление определенного интеграла
- •1. Непосредственное интегрирование.
- •2. Интегрирование по частям определенного интеграла
- •3. Замена переменной в определенном интеграле
- •Решение задач I типового варианта
- •6. Вычисление несобственных интегралов
- •Решение задач II типового варианта
- •7. Приложение определенных интегралов к задачам геометрии
- •1. Вычисление площадей плоских фигур
- •2. Вычисление объемов тел вращения
- •3. Вычисление длин плоских кривых при различных способах задания линий основные понятия и формулы
- •Решение задачи III типового варианта
- •Решение задачи IV типового варианта
- •Знания и умения, которыми должен владеть студент
- •1. Знания на уровне понятий, определений, описаний, формулировок
- •Содержание
- •Учебно-методическое пособие для выполнения индивидуального задания определенный интеграл
Решение задач II типового варианта
Вычислить несобственные интегралы или доказать их расходимость.
▲
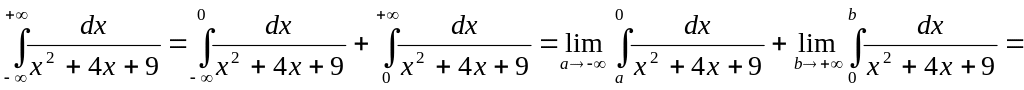
![]()
![]()
![]() .
.
Данный несобственный интеграл сходится. ▼
▲

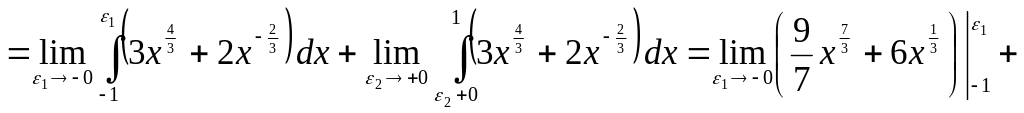
![]() .
.
Данный несобственный интеграл сходится. ▼
7. Приложение определенных интегралов к задачам геометрии
Определенный интеграл, вследствие абстрактности его понятия, широко применяется для вычисления различных геометрических и физических величин.
Величины, которые можно найти с помощью определенного интеграла, должны обладать свойством аддитивности.
Величина
![]() называется аддитивной относительно
называется аддитивной относительно
![]() ,
если
,
если
![]() вытекает
вытекает
![]() .
.
Аддитивными величинами являются площадь, объем, длина дуги, площадь поверхности вращения, работа, давление и др.
Существуют две схемы применения определенного интеграла для определения различных величин. Одна из них, повторяющая алгоритм получения определенного интеграла по заданной функции, наиболее приемлема в теории. Другая схема носит название дифференциального метода и наиболее приемлема в практике.
Для
определения какой-либо величины
![]() по дифференциальному методу нужно:
по дифференциальному методу нужно:
Найти дифференциал этой величины
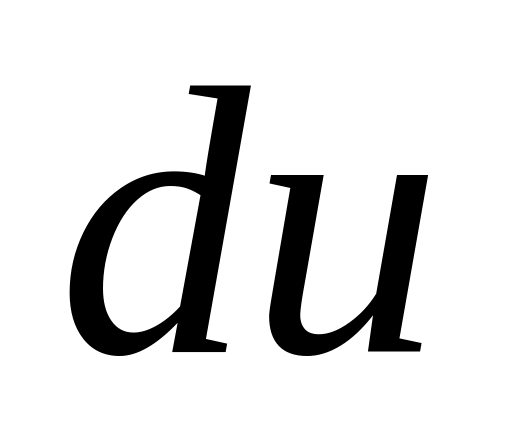 из условий задачи, как главную часть
приращения функции
из условий задачи, как главную часть
приращения функции
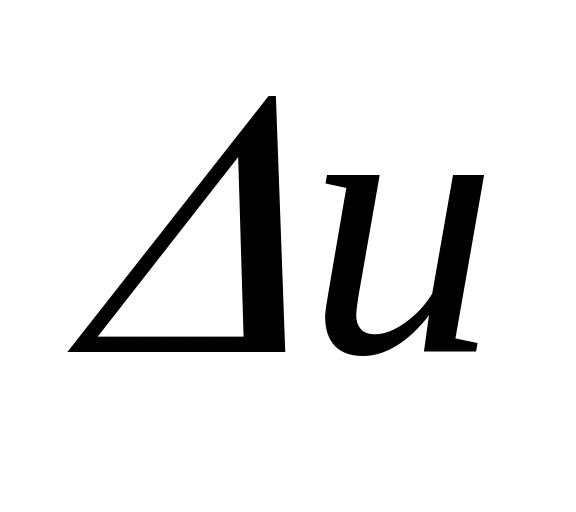
Определить пределы интегрирования, если они не заданы,
 .
.Вычислить интеграл
 .
.
1. Вычисление площадей плоских фигур
Плоской фигурой будем называть любое ограниченное множество точек плоскости.
Так как площадь – аддитивная величина, то ее можно вычислить с помощью определенного интеграла.
Воспользуемся дифференциальным методом.
Найти дифференциал площади
 .
.Определить пределы интегрирования
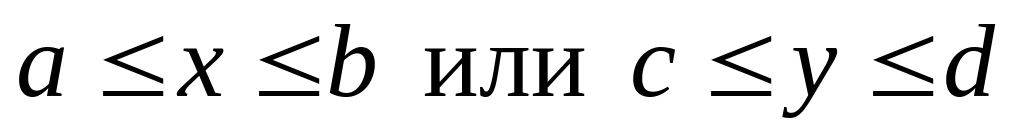 .
.Вычислить площадь
 .
.
Перед решением задачи на вычисление площадей необходим чертеж, для построения которого нужно исследовать поведение функции или воспользоваться тем, что вид графика известен, и построить линию по нескольким точка
Вычисление площади в прямоугольной системе координат. Дифференциал площади в прямоугольной системе координат – площадь прямоугольника с бесконечно малым основанием и переменной высотой. Форма записи дифференциала зависит от способа задания фигуры, от условий задачи.
Пусть
![]() –
прямоугольная декартова система
координат. Фигуры будем задавать с
помощью неравенств или систем неравенств.
–
прямоугольная декартова система
координат. Фигуры будем задавать с
помощью неравенств или систем неравенств.
Определение.
Область называется правильной
(стандартной)
относительно оси
![]() ,
если любая горизонтальная (вертикальная)
прямая пересекает границу области не
более чем в двух точках.
,
если любая горизонтальная (вертикальная)
прямая пересекает границу области не
более чем в двух точках.
Если область правильная относительно
осей
![]() ,
то она просто называется правильной
областью.
,
то она просто называется правильной
областью.
 Условимся
дальше области, правильные относительно
оси
Условимся
дальше области, правильные относительно
оси
![]() ,
штриховать линиями, параллельными оси
.
,
штриховать линиями, параллельными оси
.
y





![]()
![]()


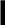

O a dx b x
![]()
Область правильная
относительно оси
![]() .
.
Если
область
![]() ,
правильная относительно оси
,
проектируется на ось
,
правильная относительно оси
,
проектируется на ось
![]() в отрезок
,
то ее граница разбивается на две линии:
нижнюю границу области, задаваемую
уравнением
в отрезок
,
то ее граница разбивается на две линии:
нижнюю границу области, задаваемую
уравнением
![]() и верхнюю, задаваемую уравнением
и верхнюю, задаваемую уравнением
![]() .
.
Тогда область определяется системой неравенств
![]()
а площадь
![]() вычисляется по формуле
вычисляется по формуле
![]() .
.
![]()
 y
y
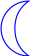



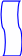 d
d


 dy
dy ![]()
![]()
c

O x
Область правильная относительно оси
![]() .
.
Если
область
,
правильная относительно оси
,
проектируется на ось
в отрезок
![]() ,
то ее граница разбивается на две линии:
левую границу области, задаваемую
уравнением
,
то ее граница разбивается на две линии:
левую границу области, задаваемую
уравнением
![]() и правую, задаваемую уравнением
и правую, задаваемую уравнением
![]() .
В этом случае область
определяется системой неравенств
.
В этом случае область
определяется системой неравенств
![]()
а площадь вычисляется по формуле
![]() .
.
Задача
7.1.1. Найти площадь фигуры,
ограниченной линиями
![]() .
.
▲
![]() – парабола;
– парабола;
![]() – прямые линии.
– прямые линии.
Найдем точки пересечения данных линий:
![]()
Построение очевидно.


 y
y
![]() B
B
![]()


 A
A


O dx C x
Найдем
![]() .
.
Область
![]() ,
правильная относительно оси
,
правильная относительно оси
![]() ,
определяется системой неравенств
,
определяется системой неравенств
![]()
![]() .
▼
.
▼
Замечание. Единицы измерения площадей всюду опускаются (для простоты).
Задача
7.1.2. Найти площадь фигуры,
ограниченной линиями
![]() .
.
▲
![]() – парабола, которая
строится по трем точкам: вершина
определяется из условия
– парабола, которая
строится по трем точкам: вершина
определяется из условия
![]() .
.
![]() .
.
Точки
пересечения с осью
![]() :
:
![]() .
.
![]() – прямая, которая
строится по двум точкам, в качестве
которых возьмем точки пересечения
данных линий:
– прямая, которая
строится по двум точкам, в качестве
которых возьмем точки пересечения
данных линий:
![]()
![]() .
.

y

 C
10
C
10
4
![]()
![]()


–2 O dx 2 B x
A D
1)
Имеем:
![]() .
.
2) Область , правильная относительно оси , определяется системой неравенств
![]()
3)
![]() .
▼
.
▼
Задача
7.1.3. Найти площадь фигуры,
ограниченную параболой
![]() и осью
.
и осью
.
▲
![]() – парабола, которая
строится по трем точкам: вершина
определяется из условия
– парабола, которая
строится по трем точкам: вершина
определяется из условия
![]() .
.
![]()
Точки пересечения с осью :
![]() .
.
![]() y
y
 C
C
 A
A
dy
 B
B
O x
1) Найдем
![]() .
.
2) Область , правильная относительно оси , определяется системой неравенств
![]()
3)
![]() .
▼
.
▼
Задача
7.1.4. Найти площадь фигуры,
ограниченной линиями
![]() .
.
▲
![]() – парабола, которая
строится по трем точкам: вершина
определяется из условия
.
– парабола, которая
строится по трем точкам: вершина
определяется из условия
.
![]() .
.
Точки пересечения с осью :
![]() .
.
![]() – прямая, которая
строится по двум точкам, в качестве
которых возьмем точки пересечения
данных линий:
– прямая, которая
строится по двум точкам, в качестве
которых возьмем точки пересечения
данных линий:
![]()
![]() .
.


y
![]()
C


 A
A
![]() O B
4 x
O B
4 x
 dy
dy
–3 D
1) Имеем
![]() .
.
2) Область , правильная относительно оси , определяется системой неравенств
![]()
3)
![]() .
▼
.
▼
Вычисление площадей при параметрическом задании линий, ограничивающих фигуру. В задачах такого типа последовательность действий сохраняется, чаще всего усложняется отыскание пределов.
Пусть
граница плоской области фигуры
– простая замкнутая кривая, заданная
параметрически уравнениями
![]() ,
причем точка
,
причем точка
![]() при изменении
при изменении
![]() границу области
так, что фигура
остается слева от движущейся точки.
Тогда площадь фигуры
может быть вычислена по любой из следующих
формул:
границу области
так, что фигура
остается слева от движущейся точки.
Тогда площадь фигуры
может быть вычислена по любой из следующих
формул:
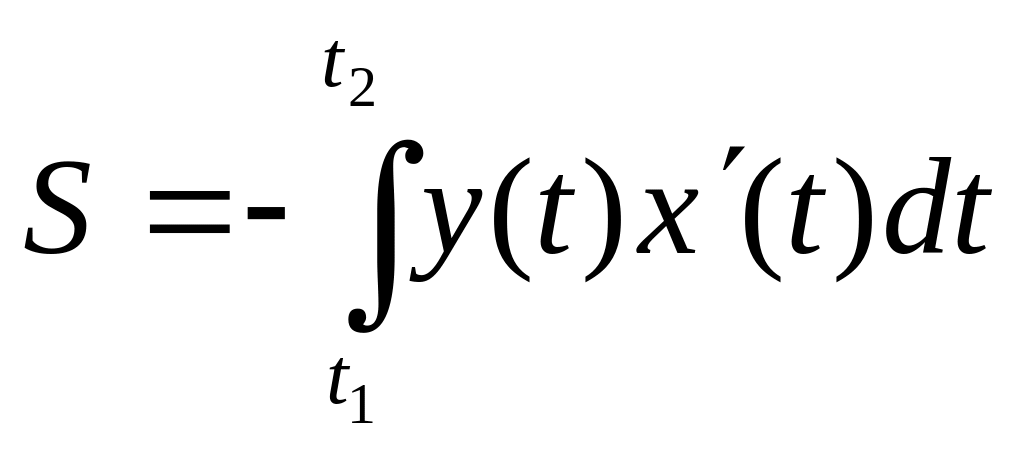 ,
,
 ,
,
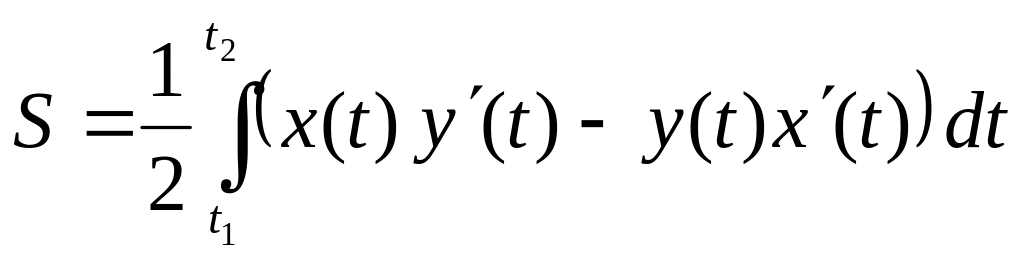 .
.
Задача
7.1.5. Найти площадь эллипса:
![]() .
.
▲ Чертеж очевиден.
y

 b
b

O dx a x
1) Имеем
![]() .
.
2)
С учетом свойств симметрии фигуры при
определении
![]() пределы находим по изменению
пределы находим по изменению
![]()
|
|
|
|
|
0 |
3)
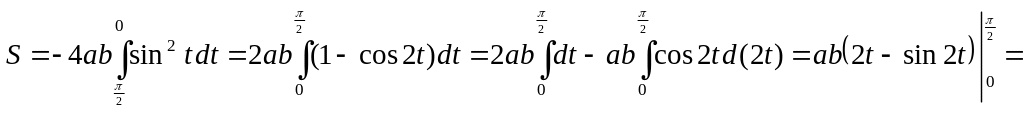
![]() .
▼
.
▼
Вычисление площадей в полярной системе координат. Вычисление площадей в полярной системе координат производится по дифференциальному методу без каких-либо изменений в его операциях и их последовательности.
Дифференциалом площади
в полярной системе координат является
площадь кругового сектора с бесконечно
малым центральным углом
![]() и переменным радиусом
и переменным радиусом
![]() :
:
![]() .
.
Форма записи дифференциала площади зависит от способа задания фигуры в полярной системе координат.
I .
.
![]() II.
II.
![]()
![]()


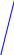
![]()



 dφ
dφ
dφ
dφ
![]()




 β β
β β

 α α
α α

O p O p
![]()
![]()
Задача
7.1.6. Найти площадь фигуры,
ограниченной лемнискатой Бернулли
![]() .
.
▲ Напоминаем, что в полярной системе координат чертеж строится по точкам.
Сначала выясняется,
где расположена линия по признаку
![]() :
:
![]() .
.
Затем по периодичности косинуса находим количество петель. Здесь их 2.
Находится
![]() по условию
по условию
![]() .
.
Построение графика очевидно.


![]()







 O 2 p
O 2 p
![]()
Далее все операции совпадают с действиями, рассмотренными раньше.
1)
![]() .
.
2)
Пределы по условию существования функции
![]() .
.
Или
с учетом свойств симметрии фигуры при
определении
пределы находим:
![]() .
.
3)
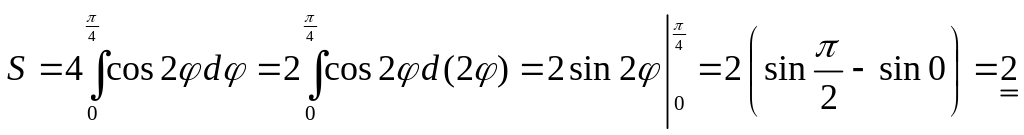
Замечание.
Кривые вида
![]() называются розами. Розы имеют
называются розами. Розы имеют
![]() лепестков (петель), если
лепестков (петель), если
![]() ,
и
,
и
![]() петель, если
петель, если
![]() .
.
Например,
![]() – трехлепестковая роза,
– трехлепестковая роза,
![]() – четырехлепестковая роза.
– четырехлепестковая роза.
При вычислении площадей, ограниченных розами, достаточно найти площадь одного лепестка и затем ее умножить на число лепестков.
