51. Понятие критерия. Критическая область и область принятия гипотезы. Односторонняя и двусторонняя критическая область, критические точки. Мощность критерия.

Статистический критерий — случайная величина R с известным законом распределения, служащая для проверки нулевой гипотезы.

Статистический критерий — строгое математическое правило, по которому принимается или отвергается та или иная статистическая гипотеза. Построение критерия представляет собой выбор подходящей функции от результатов наблюдений (ряда эмпирически полученных значений признака), которая служит для выявления меры расхождения между эмпирическими значениями и гипотетическими.

Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.

Областью принятия гипотезы (областью допустимых значений) называют совокупность значений критерия, при которых гипотезу принимают.

Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области – гипотезу отвергают, если области принятия гипотезы – гипотезу принимают.

Так как критерий K – одномерная случайная величина, то все ее возможные значения принадлежат некоторому интервалу и, соответственно, должны существовать точки, разделяющие критическую область и область принятия гипотезы. Такие точки называются критическими точками.

Различают одностороннюю (правостороннюю левостороннюю) и двустороннюю критические области.

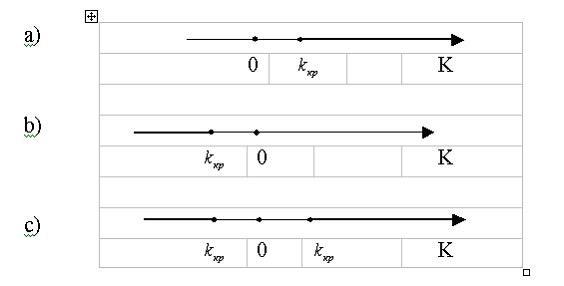
Правосторонней(а) называют критическую область, определяемую неравенством  , где   – положительное число.

Левосторонней(b) называют критическую область, определяемую неравенством  , где   – отрицательное число.

Двусторонней(c) называют критическую область, определяемую неравенствами  , где  . В частности, если критические точки симметричны относительно нуля, двусторонняя критическая область определяется неравенствами   или равносильным неравенством  .

Мощностью критерия называется вероятность попадания критерия в критическую область, при условии, что верна конкурирующая гипотеза (т.е. гипотеза противоположная нулевой). 52. Законы распределения "хи-квадрат", Стьюдента, Фишера. 

χ²-распределение, хи-квадрат распределение,  с n степенями свободы - распределение вероятностей, заданное плотностью вероятностей где Γ(λ) - гамма-функция. 

Случайная величина   имеет распределение хи-квадрат с   степенями свободы, если плотность ее распределения имеет вид:

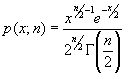
Хи-квадрат распределение с n степенями свободы может быть выведено как распределение суммы квадратов   n независимых случайных величин x₁, x₂, ..., x_n, имеющих стандартное нормальное распределение с параметрами 0 и 1. Сумма независимых случайных величин   с n₁, n₂, ..., n_k степенями свободы, соответственно, подчиняется хи-квадрат распределению с n = n₁ + n₂ + ... + n_k степенями свободы.

Сумма независимых случайных величин, имеющих распределение хи-квадрат, тоже подчинена закону распределения хи-квадрат с числом степеней свободы, равной сумме степеней свободы случайных величин, составляющих сумму.

Распределение Стьюдента

Пусть случайная величина x имеет стандартное нормальное распределение, а случайная величина c _n² - c ²-распределение с n степенями свободы.

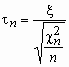
Если x и c _n² - независимы, то про случайную величину  говорят, что она имеет распределение Стьюдента с n степенями свободы. Плотность вероятности этой случайной величины вычисляется по формуле:

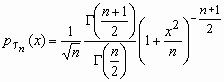, x   R, Mt _n = 0, Dt _n = n/(n-2), n>2.

При больших n распределение Стьюдента практически не отличается от N(0, 1).

Распределение Фишера

Пусть случайные величины c _n²и c _m² независимы и имеют распределение c ² с n и m степенями свободы соответственно.

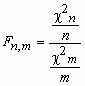
Тогда о случайной величине говорят, что она имеет F-распределение. Плотность вероятности этой случайной величины вычисляется по формуле:

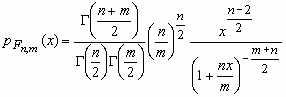, x>0, 

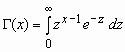 - гамма-функция Эйлера;

  , m>2; 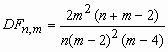 , m > 4. 53. Критерии и правила проверки гипотез: о равенстве дисперсий и математических ожиданий двух нормальных генеральных совокупностей; о том, что генеральная совокупность распределена по нормальному закону.

Проверка гипотезы о равенстве математических ожиданий  двух генеральных совокупностей

Пусть из каждой из двух нормально распределенных генеральных совокупностей   (с параметрами  ) и   (с параметрами  ) извлечены выборки объема   и   соответственно. Требуется проверить нулевую гипотезу   о равенстве средних значений этих генеральных совокупностей. Альтернативная гипотеза формулируется в соответствии с условиями задачи или эксперимента:

 (двустороння критическая область);

 (левостороння критическая область);

 (правостороння критическая область).

Случай, когда дисперсии генеральных совокупностей   и   известны. В этом случае для проверки нулевой гипотезы используют случайную величину

,

где   – выборочные средние первой и второй выборок соответственно. Если нулевая гипотеза справедлива, то статистика   имеет нормальное распределение с математическим ожиданием, равным нулю и дисперсией, равной единице . Критическое значение выбирается в соответствии с задаваемым уровнем значимости по таблице значений функции Лапласа или стандартного нормального распределения.

Если объемы выборок достаточно велики  , то случайную величину   можно использовать и при неизвестных дисперсиях генеральных совокупностей, положив в выражении для    ,  .

Эту же статистику используют и при проверке гипотезы о равенстве вероятностей «успеха». Объемы выборок   должны быть достаточно велики, чтобы биномиальное распределение можно было бы приближенно считать нормальным.

 

Проверка гипотезы о равенстве дисперсий  двух генеральных совокупностей

Пусть из двух нормально распределенных генеральных совокупностей извлечены выборки объема   и   соответственно. По этим выборкам вычислены несмещенные оценки дисперсий   и  . Для проверки нулевой гипотезы о равенстве дисперсий генеральных совокупностей   против одной из альтернативных (  – двусторонняя критическая область,   или   – односторонняя критическая область) используется случайная величина

,

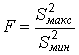здесь в числителе дроби стоит максимальная оценка дисперсии из   и  , в знаменателе – минимальная. Если нулевая гипотеза верна, то статистика   распределена по закону Фишера-Снедекора как отношение двух случайных величин, имеющих распределение   и   (  – число степеней свободы числителя;   – число степеней свободы знаменателя).

Действительно, если  , для определенности будем полагать  , то

где  ,  .

 По таблице распределения Фишера-Снедекора (прил. 5) для заданного уровня значимости   определяется критическое значение статистики   для двусторонней критической области и   – для односторонней критической области.

Вычисленное значение статистики   сравнивается с критическим. Если  , то при уровне значимости   нулевую гипотезу считают непротиворечащей опытным данным. Если же  , то нулевая гипотеза отвергается в пользу конкурирующей. 54. Функциональная, статистическая и корреляционная зависимости.

Функциональной зависимостью называется связь между двумя величинами, при которой изменение одной из них вызывает изменение другой.

Графическим изображением анализируемой зависимости (полученным путем соединения непрерывной линией точек, соответствующих данным таблицы) служит прямая линия. Такая зависимость называется прямой пропорциональной зависимостью. Ее аналитическим выражением является уравнение y=kx, где k — коэффициент пропорциональности.

Функциональная зависимость представляет собой частный случай корреляционной.

Статистическая зависимость между двумя переменными, при которой каждому значению одной переменной соответствует определённое условное математическое ожидание (среднее значение) другой, называется корреляционной. Возникновение понятия статистической связи обусловливается тем, что зависимая переменная подвержена влиянию неконтролируемых или неучтённых факторов, а также тем, что измерение значений переменных неизбежно сопровождается некоторыми случайными ошибками.

В отличие от функциональной зависимости, когда каждому значению одного признака всегда соответствует определенное значение другого, при статистической зависимости одному и тому же значению одного признака могут соответствовать различные значения другого. Это происходит в силу того, что при статистической зависимости связь устанавливается между признаками (двумя, тремя и т. д.), которые изменяются не только в силу взаимодействия между собой, но и под воздействием множества различных неучтенных факторов. В результате множественного воздействия взаимно переплетающихся факторов связь между признаками существует и проявляется не в каждом отдельном случае, как при функциональной связи, а только в тенденции, «в среднем». Поэтому здесь установить наличие взаимосвязи и определить ее количественную меру можно не на основе единичных наблюдений, а лишь применительно к определенной совокупности объектов, т. е. в среднем по отношению к тем или иным массовым объектам или явлениям. Характеризующие эти объекты количественные показатели в источниковедении и в статистике называются массовыми данными.

При функциональной зависимости с изменением значений некоторой переменной xоднозначно изменяется определенное значение переменной y, при корреляционной – определённое среднее значение (математическое ожидание) y, а при статистической – определённое распределение переменной y. Каждая корреляционная зависимость является статистической, но не каждая статистическая зависимость является корреляционной.    Статистические связи между переменными можно изучать методами корреляционного и регрессионного анализа. Основной задачей корреляционного анализа является выявление связи между случайными переменными и оценка её степени. Основной  задачей регрессионного анализа является установление формы и изучение зависимости между переменными.

Корреляционная зависимость между х и у называется линейной, если обе линии регрессии ( а; по у и у по х) являются прямыми. 

Корреляционная зависимость отражает закон множественности причин и следствия. Поэтому при изучении характера связи явлений приходится из многих причин выделять главные, решающие. 

Корреляционная зависимость между случайными величинами ( A, Y) называется линейной корреляцией, если обе функции регрессии р ( х) и g ( y) будут линейными. В этом случае линии регрессии являются прямыми и называются прямыми регрессиями.  55. Условное математическое ожидание. Коэффициент корреляции и его свойства.

Условным математическим ожиданием дискретной случайной величины Y при X =x (х – определенное возможное значение Х) называется произведение всех возможных значений Y на их условные вероятности. Для непрерывных случайных величин, где f(y/x) – условная плотность случайной величины Y при X=x.

Условное математическое ожидание M(Y/x)=f(x) является функцией от х и называется функцией регрессии Х на Y.

Свойства условного математического ожидания:

1)   2)   для любого действительного с;  3)   для любых действительных  и    4)   5)   для выпуклых функций g(x).

6) если   -тривиальная   -алгебра, то    7)    8)   9) если X не зависит от   -алгебры   то    10) если Y измерима относительно   -алгебры   то   

Корреляция определяет степень, с которой значения двух переменных «пропорциональны» друг другу. Пропорциональность означает просто линейную зависимость. Корреляция высокая, если на графике зависимость «можно представить» прямой линией (с положительным или отрицательным углом наклона). Таким образом, это простейшая регрессионная модель, описывающая зависимость одной переменной от одного фактора.

В производственных условиях обычно информации, полученной из диаграмм рассеяния при условии их корректного построения, бывает достаточно для того, чтобы оценить степень зависимости у от х. Но в ряде случаев требуется дать количественную оценку степени связи между величинамих и у. Такой оценкой является коэффициент корреляции.

Основные характеристики этого показателя.

• Он может принимать значения от –1 до +1. Знак «+» означает, что связь прямая (когда значения одной переменной возрастают, значения другой переменной также возрастают), «–» означает, что связь обратная.

• Чем ближе коэффициент к |1|, тем теснее линейная связь. При величине коэффициента корреляции менее 0,3 связь оценивается как слабая, от 0,31 до 0,5 – умеренная, от 0,51 до 0,7 – значительная, от 0,71 до 0,9 – тесная, 0,91 и выше – очень тесная.

• Если все значения переменных увеличить (уменьшить) на од­но и то же число или в одно и то же число раз, то величина коэф­фициента корреляции не изменится.

• При r=±1 корреляционная связь представляет линейную функциональную зависимость. При этом все наблюдаемые значения располагаются на общей прямой. Её ещё называют линией регрессии.

• При r=0 линейная корреляционная связь отсутствует. При этом групповые средние переменных совпадают с их общи­ми средними, а линии регрессии параллельны осям координат.