3.3.2. Ограничения на глубину связи в схеме
Формализуем понятие глубины связей в схемах следующим образом. Рассмотрим схемы, не имеющие обратных связей. Элементы таких схем можно однозначно разбить на группы, называемые рангами или ярусами, по следующему правилу. К нулевому ярусу (рангу) относим входные полюса схемы. Элементы, входы которых связаны только с входными полюсами, отнесем к первому ярусу. В общем, к элементу i-го яруса отнесем все элементы, входы которых связаны только с выходами элементов (i --1)-го и, может быть, элементов нижних ярусов. Если выход элемента i-го уровня связан с входом элемента j-го уровня, то длину этой связи оценим числом (i - j), названным глубиной связи. Если на схему задано ограничение на глубину связи, это означает, что рассматриваются только такие схемы, в которых глубина связи не превосходит заданной величины
Если рассматривать модель схемы, в которой функционирование происходит в дискретном времени по тактам и элементам приписаны единичные задержки, то ранг элемента определяет такт, в котором на его выходе реализуется выходной сигнал, а ограничение на глубину связей определяет максимальный разброс времени поступления дискретных сигналов на входы элементов схемы, равный (-1). Если = 1, то величина этого разброса равна нулю.
Определим, как изменятся требования к множеству функций, порождающих класс всех булевых функций, если рассматривать только такие их суперпозиции, которым соответствуют схемы с ограниченной глубиной связи, в частности схемы с глубиной, равной единице.
Вслед за Постом, определим булеву функцию как -функцию, если f(x,x,x,...x) = x, -функцию, если f(x,x,...,x)=1, - функцию, если f(x,x,...,x) = 0 и как - функцию, если f(x,x,...,x) = `x , где `x -инверсия х.
Очевидно, что если базис содержит хотя бы одну -функцию, он является функционально полным при условии, что глубина связи =1, так как из этой функции реализуется функция, равная переменной (повторитель или задержка), и, следовательно, любую связь можно свести введением этих функций к последовательности связей единичной глубины.
Теорема. Любой полный базис из более чем одной функции порождает С при = 1, за исключением случая, когда базис содержит ровно две функции : функцию нелинейную и несамодвойственную и функцию, не сохраняющую константу, причем последняя не равна константе и не есть -функция. Одноэлементный базис при условии = 1 неполон.
Следующие утверждения будут нам необходимы при доказательстве:
У1. Если функция самодвойственная, то она или - или -функция. Утверждение следует из того, что f(0,0,...,0) f(1,1,...,1).
У2. Линейная функция есть - или -функция тогда и только тогда, когда она самодвойственная, - или -функция тогда и только тогда, когда она несамодвойственная. Утверждение следует из определения линейной функции и того, что в первом случае сумма будет содержать нечетное число сомножителей, во втором случае – четное.
У3. Если - или -функция отлична от константы, то она немонотонна. Утверждение следует из того, что эта функция будет иметь одинаковые значения на нулевом и единичном наборах, которые сравнимы со всеми наборами и являются, соответственно, максимальным и минимальным.
У4. -функция является немонотонной и не сохраняет константы.
У5. Из линейной функции заменой некоторых переменных на константу 0 можно получить переменную (-функцию). Из нелинейной функции для получения -функции необходимо иметь обе константы.
Доказательство проведем в несколько этапов. Вначале покажем, что если базис содержит более двух элементов, то среди его функций обязательно есть -функция, то есть он полон при Затем более подробно разберем двухэлементные базисы, не содержащие функций. В конце доказательства рассмотрим одноэлементные базисы.
Пусть базис i | i=1,ки к > 2. Покажем, что он содержит функцию.
Разделим базисы на две группы в зависимости от того, какова в нем нелинейная функция (обозначим ее как 1):
а. 1 является самодвойственной;
б. 1 – функция несамодвойственная.
Случай а. По свойству 1 функция 1 или - или -функция. Если это- -функция, то она немонотонная, не сохраняет константы, и в базис достаточно добавить несамодвойственную функцию, то есть базис будет иметь только две функции.
Случай б. Если 1 -функция, то она по свойству У4 одна является полным базисом. Если 1 - или -функция, то по свойству У3 она немонотонна и не сохраняет одну константу. В этом случае в базис нужно добавить только функцию, не сохраняющую вторую константу.
Утверждение 1 доказано. Рассмотрим теперь базисы, содержащие ровно две функции и не содержащие -функций. Обозначим их как ={1, 2}.
Снова разделим рассмотрение на два случая: а) функция 1 –несамодвойственная и линейная, 2 - функция самодвойственная и нелинейная. Случай б) функция 1 – несамодвойственная и нелинейная, 2 - не сохраняет константу.
Случай а). По свойству У2 функция 2 является -функцией, значит на втором уровне можно получить инверсии переменных. Функция 1 является - или -функцией, значит на втором уровне можно получить одну из констант. На третьем уровне с помощью этих функций получаем переменные и обе константы (вторую – через инверсию первой). С помощью констант из линейной функции можно получить на четвертом и всех последующих уровнях -функцию (повторитель), чем и обеспечивается полнота базиса для этого случая.
Случай б.
функция 1 – несамодвойственная, нелинейная и не -функция (иначе она одна – базис). Значит это - или -функция. Если при этом 2 есть - или -функция , то на втором уровне можно получить только такие функции, которые имеют значения на нулевом наборе такие же, как и на единичном. Значит, на следующих уровнях из них не удастся получить - или -функции и полнота обеспечена не будет.
Если же функция 2 есть -функция, то на втором уровне могут быть получены инверсии переменных и константа, на третьем – переменные и обе константы, которые позволят по свойству У5 получить повторитель на всех последующих уровнях.
И, наконец, если функция 2 есть константа, то она есть на первом уровне вместе с переменными. С ее помощью из функции 1 можно получить на втором уровне инверсии переменных и обе константы, которые обеспечат полноту.
Для одноэлементного базиса, реализующего только -функцию, на первом ( и всех нечетных ) уровне можно реализовать только -функции, на втором (и всех четных) уровне реализуются только -функции. В этом базисе при никогда не реализуются и функции. Значит, полнота обеспечена быть не может.
При функциональная полнота обеспечивается для любого функционально полного в смысле Поста базиса.
Теперь понятно, почему нельзя реализовать любую функцию из элементов шефферовского типа в однородных двумерных решетках как на рис.3.4
Здесь любая схема будет иметь , и для получения схем с глубиной связи, равной двум, нужно решетку дополнить диагональными связями,
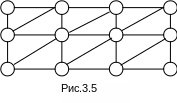
например, как это показано на рис. 3.5.