
- •Проектирование автоматов
- •Проектирование автоматов
- •5.7. Упражнения 90
- •Введение
- •1. Абстрактные автоматы
- •1.1. Эквивалентность автоматов
- •1.2. Минимизация автоматов
- •1.2.1. Минимизация полностью определенного автомата
- •1.2.2. Минимизация частичного автомата
- •1.3. Композиция автоматов
- •1.3.1. Параллельное соединение
- •1.3.2. Последовательное соединение
- •1.3.3. Соединение с обратной связью
- •1.3.4. Соединение в сеть
- •1.4 Декомпозиция автомата
- •1.4.1. Задача декомпозиции
- •1.4.2. Разбиения со свойствами подстановки
- •1.4.3. Метод декомпозиции
- •1.5. Упражнения Эквивалентность автоматов
- •Минимизация полностью определённого автомата.
- •Декомпозиция автоматов
- •2. Структурные автоматы
- •2.1. Автоматная полнота и теорема в.М.Глушкова
- •2.2. Гонки в автомате
- •2.2.1. Кодирование состояний
- •2.2.2. Понятие о гонках. Противогоночное кодирование
- •2.3. Проектирование автомата
- •2.4. Упражнение Кодирование
- •Синтез автомата
- •3. Синтез схем
- •3.1. Определения
- •3.2. Функциональная полнота базиса
- •3.2.1. Классы функций
- •3.2.2. Монотонные функции
- •3.2.3. Самодвойственные функции
- •3.2.4. Линейные функции
- •3.2.5. Функции, сохраняющие константу
- •3.2.6. Функциональная полнота
- •3.3. Топологические ограничения в схемах
- •3.3.1. Плоские схемы
- •3.3.2. Ограничения на глубину связи в схеме
- •3.4. Методы синтеза схем
- •3.4.1. Метод факторизации
- •3.4.2. Метод декомпозиции
- •3.4.3. Синтез схем в классическом базисе.
- •3.4.4. Синтез схем в монофункциональном базисе.
- •3.5. Упражнения Функциональная полнота
- •Синтез схем
- •4. Эксперименты над автоматами
- •4.1. Построение диагностических деревьев
- •4.2. Диагностические и установочные эксперименты
- •4.2.1. Дерево преемников
- •4.2.2. Диагностический эксперимент
- •4.2.3. Установочный эксперимент
- •4.3. Упражнения Диагностические эксперименты
- •Установочные эксперименты
- •5. Формальные грамматики
- •5.1. Языки и порождающие их грамматики
- •5.2. Примеры фрагментов описаний в языках программирования.
- •5.3. Порождающая грамматика
- •5.4. Классы языков и грамматик
- •5.5. Язык, понимаемый устройством
- •5.6. Автоматные языки
- •5.7. Упражнения
- •Библиографический список
- •Проектирование автоматов
- •620002, Екатеринбург, Мира, 19
3.4. Методы синтеза схем
Рассмотрим два подхода к синтезу схем – декомпозицию и факторизацию.
3.4.1. Метод факторизации
Метод факторизации заключается в алгебраических преобразованиях описаний, заданных для реализации функций, с тем, чтобы выразить их через функции базиса. При этом важной частью преобразований является учёт числа входов элементов базиса, что обеспечивается вынесением за скобки и использованием свойств дистрибутивности функций.
Рассмотрим применение метода для классического базиса, состоящего из элементов {2-И, 2-ИЛИ, НЕ}, и для монофункциональных базисов {И-НЕ} или {ИЛИ-НЕ.}
3.4.2. Метод декомпозиции
Метод декомпозиции ещё называют методом от выходов к входам. Он состоит из последовательности шагов:
Определяется множество функций, называемых множеством непостроенных функций (обозначим как Fн). Вначале Fн=F.
Выбирается функция fFн и она удаляется из Fн. Выбирается элемент . Предполагается, что f реализуется на выходе элемента .
Определяются функции (называемые образующим списком), которые необходимо подать на вход элемента , чтобы на выходе его получить f.
Эти функции, за исключением входных переменных, вносятся в множество Fн.
Шаги 2 -4 повторяются до тех пор, пока множество Fн не станет пустым. Для того чтобы получить решение, любая из функций образующего списка для f должна быть проще функции f. Самыми простыми считаются входные переменные, для других функций каждый метод предлагает своё понятие простоты.
Рассмотрим работу метода на примере реализации функции сложения по модулю два от двух переменных в одноэлементном базисе, состоящем из элемента 2-И-НЕ.
Запишем таблицу для элемента базиса (табл. 3.4) и перепишем её в виде табл.3.5, где символом x обозначено значение «что угодно». Например, 2-я строка таблицы означает, что если на первом входе элемента – нулевое значение, то независимо от значения на втором входе значение на выходе элемента равно единице.
Запишем функцию в векторном виде как f = (ab) = <0110>.
При построении образующего списка будем исходить из того, что для реализации на выходе элемента 0 необходимо на оба входа подать 1, для реализации 1 необходимо на один вход подать 0, на другой – что угодно. Образующий список для f в этом случае будет иметь вид {<1x01>,<10x1>}.
Таблица 3.4 |
||
a |
b |
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
Таблица 3.5 |
||
a |
b |
|
0 |
x |
1 |
x |
0 |
1 |
1 |
1 |
0 |
П
 редставим
всё решение в виде рис. 3.6. На выходе 2-го
элемента верхняя функция дополняется
до переменной b=<0011>,
нижняя функция элемента 3 – до функции
а=<0101>. На входе 5-го элемента нижняя
функция дополняется до b,
верхняя функция 4-го элемента – до а.
редставим
всё решение в виде рис. 3.6. На выходе 2-го
элемента верхняя функция дополняется
до переменной b=<0011>,
нижняя функция элемента 3 – до функции
а=<0101>. На входе 5-го элемента нижняя
функция дополняется до b,
верхняя функция 4-го элемента – до а.
Результирующая схема приведена на рис.3.7.
К методу декомпозиции можно отнести и метод каскадов Поварова, основанного на разложении К. Шеннона. Функция представляется как f(x1,x2,…,xn) = xf(x=1) xf(x=0), конструкция из элемента дизъюнкции и 2-х элементов конъюнкции образует каскад, на входе которого функции не зависят от переменной х и в этом смысле более просты, чем исходная функция.
В этом методе результат неоднозначен и зависит от порядка выбора переменных, по которым проводится разложение. Если функцию можно представить как сложение по модулю два переменной и некоторой функции f” от остальных переменных, то f” = f(x = 1) =f(x = 0).
Пример. Построим схему для функции от 4 переменных, представленную в виде вектора
f (a,
b, c,
d) = <0110100101000101>
(a,
b, c,
d) = <0110100101000101>
Начнём разложение с разложения по a. Получим f1 = f(a = 0) = <01101001>, f2 = f(a = 1) = <01000101>.
Р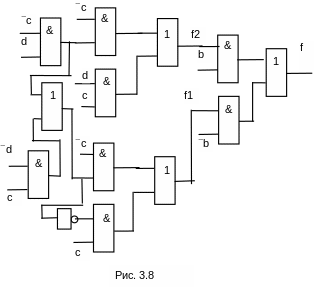 азложим
f1 по переменной b, получим
азложим
f1 по переменной b, получим
f11 = f1(b = 0) = <0110>, f12 = f1(b = 1) = <1001>.
Замечаем, что f11 =f12 = cd cd.
Эта функция не минимизируется, реализуем её в базисе
{2-И, 2-ИЛИ, НЕ}.
Разложим f2 по переменной b, получим:
f21=f2(b=0)=<0100>, f22=f2(b=1)=<0101
Замечаем, что f22=переменной d, f21 =(cd).
Окончательно решение примет вид как на рис. 3.8.
