
- •1. Предмет теории вероятностей. Случайный эксперимент.
- •2. Классическое определение вероятности.
- •3. Геометрическое определение вероятности
- •4. Аксиоматическое определение вероятности
- •5. Условные вероятности
- •6. Независимые события
- •7. Формулы полной вероятности и Байеса
- •8. Схема независимых испытаний Бернулли
- •9. Случайные величины. Функция распределения случайной величины и ее свойства
- •10. Дискретные случайные величины. Закон распределения дсв.
- •12. Непрерывные случайные величины. Плотность вероятностей
- •13. Важнейшие непрерывные случайные величины
- •1 4. Математическое ожидание св.
- •15. Моменты. Дисперсия. Среднее квадратическое отклонение.
- •16. Чх дискретных и непрерывных случайных величин
- •17. Случайные векторы. Фр случайного вектора и ее свойства.
- •18. Дискретные случайные векторы. Зр дискретного случайного вектора
- •19. Непрерывные случайные векторы. Плотность вероятностей и ее свойства
- •20. Пример. (Равномерное распределение в области ).
- •21. Независимость случайных величин
- •22. Условные законы распределения и условные числовые характеристики
- •23. Числовые характеристики случайных векторов
- •24. Теоремы о числовых характеристиках
- •25. Некоррелированность случайных величин и ее связь с независимостью
- •26. Коэффициент корреляции его свойства
- •27. Многомерное нормальное (гауссовское) распределение
- •28. Функции случайных аргументов
- •29. Композиция (свертка) законов распределения
- •30. Неравенство Чебышева
- •31. Законы больших чисел
- •32. Теорема 3 (збч для независимых, одинаково распределенных св).
- •33. Центральная предельная теорема
- •34. Теорема 2 (Ляпунова) (цпт для независимых, разнораспределенных св)
12. Непрерывные случайные величины. Плотность вероятностей
Определение. СВ
называется непрерывной или имеющей
непрерывный закон распределения
(НСВ), если существует такая функция
![]() ,
что для любого
,
что для любого
![]() ФР
ФР
![]() СВ
допускает представление:
СВ
допускает представление:
![]() .(2.3)При
этом функция
.(2.3)При
этом функция
![]() называется плотностью вероятностей
СВ
.
называется плотностью вероятностей
СВ
.
Замечание. Для существования интеграла (2.3) предполагается, что ПВ является функцией непрерывна всюду, за исключением, может быть, конечного числа точек.
Из определения следует:
1. Если СВ является непрерывной, то ее ФР непрерывна на всей числовой прямой.
Следствие. Если СВ
является непрерывной, то
![]() для любого
.
(2.4)
для любого
.
(2.4)
2. Если СВ
является непрерывной, то ее ФР
является дифференцируемой во всех
точках, где ПВ
непрерывна, и при этом справедливо
равенство![]() .
(2.5)
.
(2.5)
(Также следует из свойств интеграла с переменным верхним пределом).
В точках, где ПВ
непрерывной не является, производная
ФР
точках, где ПВ
непрерывной не является, производная
ФР
![]() не существует. Это означает, что в этих
точках ФР
,
являясь функцией непрерывной, имеет
излом, так что
не существует. Это означает, что в этих
точках ФР
,
являясь функцией непрерывной, имеет
излом, так что
![]() .
Но таких точек в соответствии с замечанием
не более конечного числа и в них ПВ может
быть задана произвольно (на величине
интеграла (2.3) и на вероятностях событий,
связанных с НСВ, в соответствии с (2.4)
это никак не отражается). Графическая
иллюстрация.
.
Но таких точек в соответствии с замечанием
не более конечного числа и в них ПВ может
быть задана произвольно (на величине
интеграла (2.3) и на вероятностях событий,
связанных с НСВ, в соответствии с (2.4)
это никак не отражается). Графическая
иллюстрация.
Из равенства (2.5) и определения производной следует, что
![]() .
.
Интерпретируя вероятность
![]() как массу, приходящуюся на интервал
как массу, приходящуюся на интервал
![]() ,
отношение
,
отношение
![]() представляет собой среднюю плотность
массы на этом интервале, а в пределе при
представляет собой среднюю плотность
массы на этом интервале, а в пределе при
![]() получаем плотность массы в точке х.
Это оправдывает использование термина
«плотность» для функции
.
Формулы (2.3) и (2.5) показывают, что между
ФР
и ПВ
существует взаимно однозначное
соответствие. Поэтому по аналогии с
дискретным случаем ПВ можно называть
ЗР НСВ.
получаем плотность массы в точке х.
Это оправдывает использование термина
«плотность» для функции
.
Формулы (2.3) и (2.5) показывают, что между
ФР
и ПВ
существует взаимно однозначное
соответствие. Поэтому по аналогии с
дискретным случаем ПВ можно называть
ЗР НСВ.
Свойства плотности вероятностей.
1.
![]() для любого
.
Поскольку ФР
является функцией неубывающей, то ее
производная
для любого
.
Поскольку ФР
является функцией неубывающей, то ее
производная
![]() .
Поэтому свойство следует из равенства
(2.5) ■.
.
Поэтому свойство следует из равенства
(2.5) ■.
2.
![]() - условие нормировки. Из представления
(2.3) следует, что
- условие нормировки. Из представления
(2.3) следует, что
![]() ,
а в соответствии со свойством 3 ФР
,
а в соответствии со свойством 3 ФР
![]() ■.
■.
3. Вероятность попадания НСВ
в интервал
определяется как интеграл от ПВ по этому
интервалу: для любых
![]() .
(2.6)
.
(2.6)
П оскольку
в соответствии со свойством 5 ФР
оскольку
в соответствии со свойством 5 ФР
![]() ,
то свойство непосредственно вытекает
из представления (2.3):
,
то свойство непосредственно вытекает
из представления (2.3):
![]() ■.
■.
Следствие. Для непрерывной СВ
![]()
и все вероятности определяются с помощью интеграла (2.6).
Графическая иллюстрация ФР и ПВ НСВ.
13. Важнейшие непрерывные случайные величины
1.
Равномерная
СВ.
Говорят, что НСВ
имеет равномерное распределение
(равномерный ЗР) на отрезке
![]() ,
если множество ее возможных значений
,
если множество ее возможных значений
![]() ,
а
ПВ
постоянна на этом отрезке:
,
а
ПВ
постоянна на этом отрезке: Константа С
при этом однозначно определяется из
условия нормировки:
Константа С
при этом однозначно определяется из
условия нормировки:
![]() ,
то есть
,
то есть
![]() .
Таким образом, равномерно распределенная
СВ имеет ПВ:
.
Таким образом, равномерно распределенная
СВ имеет ПВ: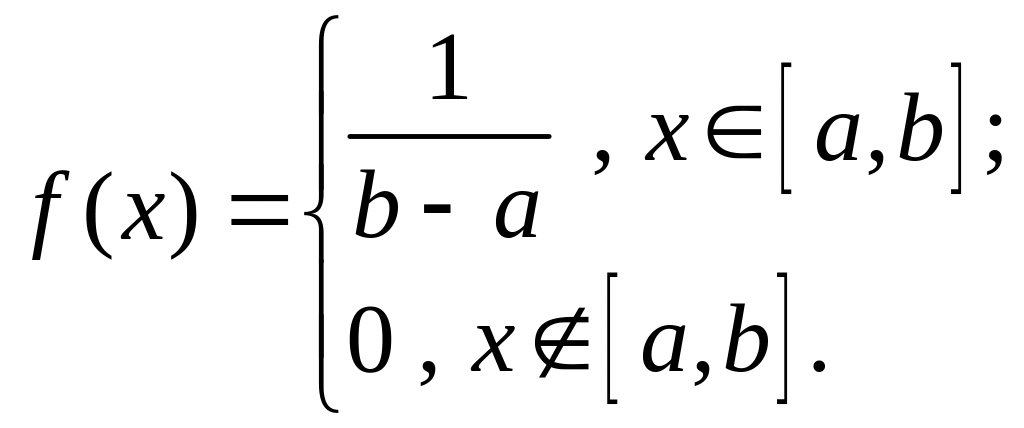 и для нее используется сокращенная
запись:
и для нее используется сокращенная
запись:
![]() .
.
Н айдем
ФР
СВ
.
Для этого рассмотрим три случая:
айдем
ФР
СВ
.
Для этого рассмотрим три случая:
а)
если
![]() ,
то
,
то
![]() ;
;
б )
если
)
если
![]() ,то
,то
![]() ;
;
в)
если
![]() ,
то
,
то
![]() .
.
Окончательно
имеем: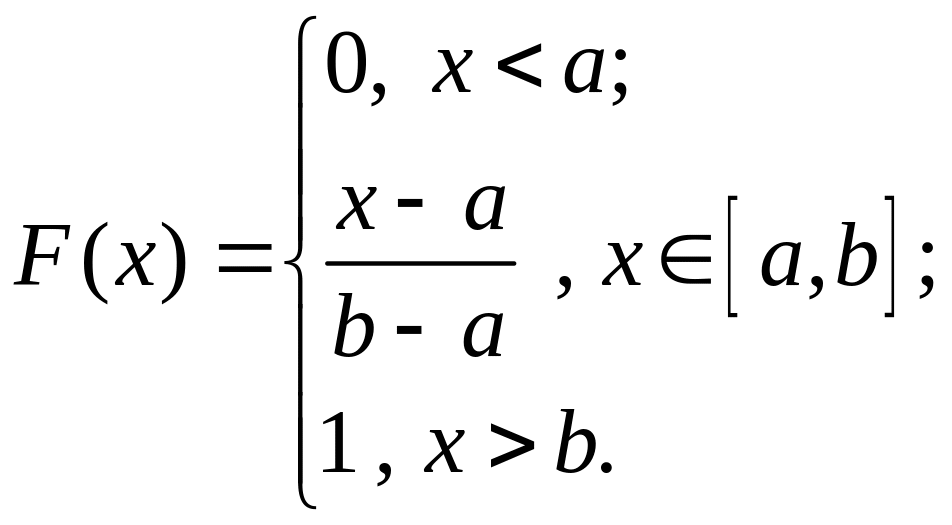 Графики
ПВ и ФР СВ
имеют вид:
Графики
ПВ и ФР СВ
имеют вид:
2.
Показательная
(экспоненциальная) СВ.
Говорят, что НСВ
имеет показательное распределение
(показательный, экспоненциальный ЗР),
если множество ее возможных значений
![]() ,
а
ПВ
имеет вид:
,
а
ПВ
имеет вид:![]()
![]() - параметр показательного распределения.
Сокращенная запись для показательной
СВ:
- параметр показательного распределения.
Сокращенная запись для показательной
СВ:
![]() .
.
Проверим
условие нормировки.
 при любом
.
при любом
.
Н айдем
ФР СВ
.
айдем
ФР СВ
.
Для этого рассмотрим два случая:
а)
если
![]() ,
то
;
,
то
;
б)
если
![]() ,
то
,
то
 .
.
Окончательно
имеем:![]() Графики ПВ и ФР СВ
имеют вид:
Графики ПВ и ФР СВ
имеют вид:
3. Нормальная (гауссовская) СВ.
![]() Говорят,
что НСВ
имеет нормальное распределение
(нормальный, гауссовский ЗР) с параметрами
Говорят,
что НСВ
имеет нормальное распределение
(нормальный, гауссовский ЗР) с параметрами
![]() ,
если множество ее возможных значений
,
если множество ее возможных значений
![]() ,
а
ПВ
имеет вид:
,
а
ПВ
имеет вид:
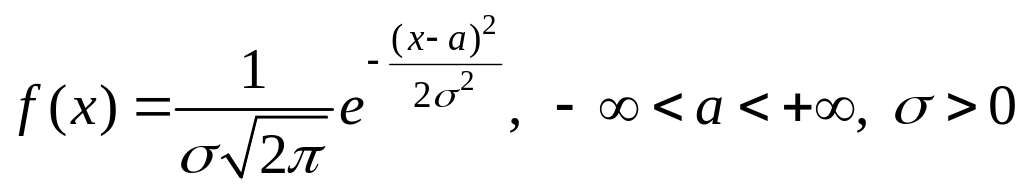
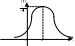 .
Сокращенная запись:
.
Сокращенная запись:
![]()
Кривая
ПВ СВ
имеет симметричный вид относительно
прямой
![]() и имеет максимум в точке
.
и имеет максимум в точке
.
Проверим
условие нормировки:
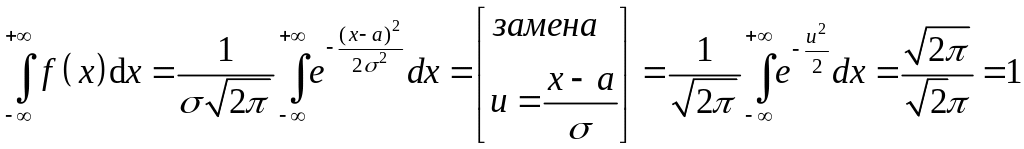
для
любых значений параметров а
и
![]() (при этом был использован известный в
анализе факт, что
(при этом был использован известный в
анализе факт, что
![]() - интеграл Пуассона).
- интеграл Пуассона).
 Е
Е сли
параметр
фиксирован, то при изменении а
кривая
,
не изменяя своей формы, просто смещается
вдоль оси абсцисс. Изменение
при фиксированном а
равносильно изменению масштаба кривой
по обеим осям: при увеличении
ПВ становится более плоской, растягиваясь
вдоль оси абсцисс; при уменьшении
- вытягивается вверх, одновременно
сжимаясь с боков (эффект действия условия
нормировки). Таким образом, параметр
является параметром масштаба. Также
параметр
характеризует степень разброса значений
СВ около среднего значения а:
при уменьшении
значения СВ
более плотно группируются около а,
то есть степень разброса значений СВ
около среднего значения а
меньше.
сли
параметр
фиксирован, то при изменении а
кривая
,
не изменяя своей формы, просто смещается
вдоль оси абсцисс. Изменение
при фиксированном а
равносильно изменению масштаба кривой
по обеим осям: при увеличении
ПВ становится более плоской, растягиваясь
вдоль оси абсцисс; при уменьшении
- вытягивается вверх, одновременно
сжимаясь с боков (эффект действия условия
нормировки). Таким образом, параметр
является параметром масштаба. Также
параметр
характеризует степень разброса значений
СВ около среднего значения а:
при уменьшении
значения СВ
более плотно группируются около а,
то есть степень разброса значений СВ
около среднего значения а
меньше.
Если
![]() и
и
![]() ,
то нормальный ЗР называется стандартным,
его ПВ имеет вид:
,
то нормальный ЗР называется стандартным,
его ПВ имеет вид:![]()
и называется функцией Гаусса. ФР СВ
называется функцией Гаусса. ФР СВ
![]() имеет вид:
имеет вид:![]() и не выражается в элементарных функциях.
Функцию
и не выражается в элементарных функциях.
Функцию
![]() называют функцией Лапласа (или интегралом
вероятностей).
называют функцией Лапласа (или интегралом
вероятностей).
Свойства
функции Лапласа
![]() :
:
1.
![]() ;
2.
;
2.
![]() для
для
![]() .
Значения функции Лапласа
для
табулированы.
.
Значения функции Лапласа
для
табулированы.
ФР СВ также выражается через функцию Лапласа :
 .
.
Вероятность
попадания СВ
в заданный интервал
![]() определяется по формуле:
определяется по формуле:
![]() .
.
Наиболее
просто выражается через функцию Лапласа
вероятность попадания СВ
в интервал длины
![]() ,
симметричный относительно точки
.
,
симметричный относительно точки
.
![]()
![]() .
.
Д алее,
если положить
алее,
если положить
![]() и учесть, что
и учесть, что
![]() ,
то получаем:
,
то получаем:
![]() .
.
Полученный
результат носит название «Правило
трех сигма».
Он означает, что «практически все»
значения СВ
находятся внутри интервала
![]() в том смысле, что вероятность СВ
принять значение, не принадлежащее
этому интервалу, пренебрежимо мала (
в том смысле, что вероятность СВ
принять значение, не принадлежащее
этому интервалу, пренебрежимо мала (![]() ).
).
4. СВ, имеющая распределение Коши.
Говорят,
что НСВ
имеет ЗР Коши, если множество ее возможных
значений
,
а
ПВ
имеет вид:![]() .
ФР СВ, распределенной по закону Коши,
имеет вид:
.
ФР СВ, распределенной по закону Коши,
имеет вид:
![]() .
.
Графики ПВ и ФР СВ, распределенной по закону Коши, выглядят следующим образом:
