
Непосредственное интегрирование
Метод интегрирования, при котором интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.
Подведение под знак дифференциала
Данный метод эквивалентен методу замены переменной (см. далее):
![]()
Если n и m чётные, то удобнее сделать подстановку tg x = t.
Интегрирование по частям — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы
для неопределённого интеграла:
![]()
для определённого:
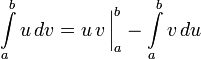
Предполагается,
что нахождение интеграла
![]() проще, чем
проще, чем
![]() .
В противном случае применение метода
неоправдано.
.
В противном случае применение метода
неоправдано.
Метод замены переменной (метод подстановки)
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть
требуется вычислить интеграл
![]() Сделаем подстановку
Сделаем подстановку
![]() где
где
![]() — функция, имеющая непрерывную
производную.
— функция, имеющая непрерывную
производную.
Тогда
![]() и на основании свойства инвариантности
формулы интегрирования неопределенного
интеграла получаем формулу интегрирования
подстановкой:
и на основании свойства инвариантности
формулы интегрирования неопределенного
интеграла получаем формулу интегрирования
подстановкой:
![]()
Рассмотрим интегралы, подынтегральная функция в которых содержит квадратный трёхчлен
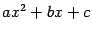 ,
где
,
где
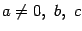 -- некоторые постоянные, вида
-- некоторые постоянные, вида
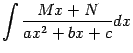 и
и
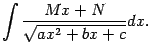
(Заметим,
что в числителе дроби должно стоять
линейное выражение
![]() ,
где
,
где
![]() и
и
![]() -- постоянные; при этом какой-либо из
постоянных не запрещается быть равной
0.)
-- постоянные; при этом какой-либо из
постоянных не запрещается быть равной
0.)
Такие интегралы приводятся к табличным следующим способом. Нужно выделить из квадратного трёхчлена выражение, равное полному квадрату, сделав такое преобразование:
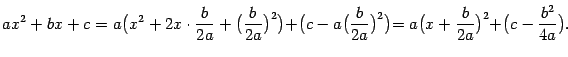
После
этого сделаем линейную замену
![]() и получим интеграл одного из видов:
и получим интеграл одного из видов:
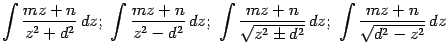
при
некоторых постоянных
![]() и
и
![]() .
Далее разбиваем интеграл на два слагаемых
и в первом, в числителе подынтегральной
функции содержащем
.
Далее разбиваем интеграл на два слагаемых
и в первом, в числителе подынтегральной
функции содержащем
![]() ,
делаем замену
,
делаем замену
![]() ,
,
![]() или
или
![]() , согласно тому, что стоит в знаменателе.
После этого первое слагаемое приводится
к табличному интегралу. Второе слагаемое,
с
, согласно тому, что стоит в знаменателе.
После этого первое слагаемое приводится
к табличному интегралу. Второе слагаемое,
с
![]() в числителе подынтегральной функции,
тоже даёт табличный интеграл.
в числителе подынтегральной функции,
тоже даёт табличный интеграл.
?????????????????????????????????????????
Интегрирование выражений вида
Если m нечётное, m > 0, то удобнее сделать подстановку sin x= t.
Если n нечётное, n > 0, то удобнее сделать подстановку cos x = t.
??????????????????????????????????????????????????????????
Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).
Данное выше определение интеграла при всей его кажущейся общности в итоге приводит к привычному пониманию определённого интеграла, как площади подграфика функции на отрезке.
Пусть
![]() определена на
определена на
![]() .
Разобьём
на части с несколькими произвольными
точками
.
Разобьём
на части с несколькими произвольными
точками
![]() Тогда говорят, что произведено разбиение
Тогда говорят, что произведено разбиение
![]() отрезка
Далее
выберем произв. точку
отрезка
Далее
выберем произв. точку
![]() ,
,
![]() ,
Определённым интегралом от функции
на отрезке
называется предел интегральных сумм
,
Определённым интегралом от функции
на отрезке
называется предел интегральных сумм
![]() при
при
![]() ,
если он существует независимо от
разбиения
и выбора точек
,
если он существует независимо от
разбиения
и выбора точек
![]() ,
т.е.
,
т.е.
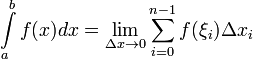 (1) Если существует (1), то
функция
называется интегрируемой на
– определение интеграла по Риману.
(1) Если существует (1), то
функция
называется интегрируемой на
– определение интеграла по Риману.
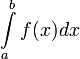
 –
нижний предел.
–
нижний предел.
 –
верхний предел.
–
верхний предел.
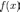 –
подынтегральная функция.
–
подынтегральная функция.
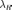 -
длина частичного отрезка.
-
длина частичного отрезка.
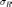 – интегральная сумма от
функции
на
соответствующей разбиению
.
– интегральная сумма от
функции
на
соответствующей разбиению
.
- максимальная длина част. отрезка.
Определение
интеграла на языке
![]() ,
,
![]() :(по
"Коши") Число I – называется
определённым интегралом от f(x) на [ a ; b
], если для любого ε>0 существует
δ=δ(ε)>0: для любого разбиения R отрезка
[ a ; b ]: λR < δ, выполняется неравенство:
|I- σR | = |∑n-1i=0f(ξi) Δxi - I| < ε при любом ξi
є [ xi ; xi+1] Тогда I = ∫abf(x)dx
:(по
"Коши") Число I – называется
определённым интегралом от f(x) на [ a ; b
], если для любого ε>0 существует
δ=δ(ε)>0: для любого разбиения R отрезка
[ a ; b ]: λR < δ, выполняется неравенство:
|I- σR | = |∑n-1i=0f(ξi) Δxi - I| < ε при любом ξi
є [ xi ; xi+1] Тогда I = ∫abf(x)dx
Определённый
интеграл
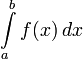 численно равен площади фигуры, ограниченной
осью абсцисс, прямыми
численно равен площади фигуры, ограниченной
осью абсцисс, прямыми
![]() и
и
![]() и графиком функции
.
и графиком функции
.
Теорема Коши
Пусть
даны две функции
и
![]() такие, что:
такие, что:
 и
определены и непрерывны на отрезке
и
определены и непрерывны на отрезке
![]() ;
;
производные
![]() и
и
![]() конечны на интервале
;
конечны на интервале
;
производные и не обращаются в нуль одновременно на интервале ;
![]()
тогда
![]() ,
где
,
где
![]()
(Если
убрать условие 4, то необходимо усилить
условие 3: g'(x) не должна обращаться в
нуль нигде в интервале
![]() .)
.)
Геометрически
это можно переформулировать так: если
и
![]() задают закон движения на плоскости (то
есть определяют абсциссу и ординату
через параметр
задают закон движения на плоскости (то
есть определяют абсциссу и ординату
через параметр
![]() ),
то на любом отрезке такой кривой, заданном
параметрами
),
то на любом отрезке такой кривой, заданном
параметрами
![]() и
и
![]() ,
найдётся касательный вектор, коллинеарный
вектору перемещения от
,
найдётся касательный вектор, коллинеарный
вектору перемещения от
![]() до
до
![]() .
.
Основные свойства определенного интеграла.
Условимся, что a < b.
1)Для функции y = f(x),
определенной при x = a, справедливо
равенство
 .
.
2)
Для интегрируемой на отрезке [a; b] функции
выполняется
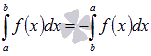 .
.
3)
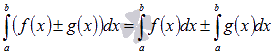 для интегрируемых на отрезке [a; b] функций
y = f(x) и y = g(x).
для интегрируемых на отрезке [a; b] функций
y = f(x) и y = g(x).
4)
остоянный множитель можно
выносить за знак определенного интеграла.
То есть, для интегрируемой на отрезке
[a; b] функции y = f(x) и произвольного числа
k справедливо равенство
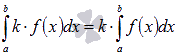 .
.
5)
Пусть функция y = f(x)
интегрируема на интервале X, причем
![]() и
и
![]() ,
тогда
,
тогда
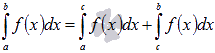 .
.
6)
Если функция интегрируема
на отрезке [a; b], то она интегрируема и
на любом внутреннем отрезке
![]() .
.
7)
Если функция y = f(x) интегрируема на
отрезке [a; b] и
![]() для любого значения аргумента
для любого значения аргумента
![]() ,
то
,
то
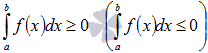 .
.
8)
Пусть функция y = f(x)
интегрируема на отрезке [a; b], тогда
справедливо неравенство
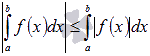 .
.
9)
Пусть функции y = f(x) и y =
g(x) интегрируемы на отрезке [a; b] и
![]() для любого значения аргумента
,
тогда
для любого значения аргумента
,
тогда
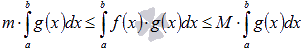 ,
где
,
где
![]() и
и
![]() .
.
10) Первая формула среднего значения.
Пусть функция y = f(x)
интегрируема на отрезке [a; b],
и
,
тогда существует такое число
![]() ,
что
,
что
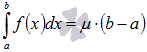 .
.
11) Вторая формула среднего значения.
Если на отрезке [a; b] функция
y = f(x) интегрируема, а y = g(x) монотонна, то
существует такое число
![]() ,
что справедливо равенство
,
что справедливо равенство
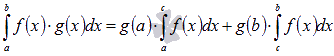 .
.
Формула Ньютона-Лейбница.
Пусть функция y = f(x)
непрерывна на отрезке [a; b] и F(x) - одна из
первообразных функции на этом отрезке,
тогда справедливо равенство
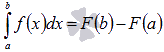 .
.
Эту формулу называют основной формулой интегрального исчисления.
Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы
для неопределённого интеграла:
для определённого:
Предполагается, что нахождение интеграла проще, чем . В противном случае применение метода неоправданно.
ТЕОРЕМА.
Пусть функция φ(t) имеет непрерывную
производную на отрезке [α,β], а=φ(α), в=φ(β)
и функция f(х) непрерывна в каждой точке
х вида х=φ(t), где t![]() [α,β].
[α,β].
Тогда справедливо следующее равенство:
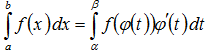
Эта формула носит название формулы замены переменной в определенном интеграле.
Площадь, заключённая между графиком непрерывной функции на интервале
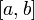 и горизонтальной осью, может быть
вычислена как определённый интеграл
от этой функции:
и горизонтальной осью, может быть
вычислена как определённый интеграл
от этой функции:
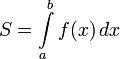
Площадь,
заключённая между графиками двух
непрерывных функций
![]() на
интервале
находится как разность определённых
интегралов от этих функций:
на
интервале
находится как разность определённых
интегралов от этих функций:
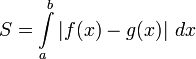
Обыкновенные дифференциальные уравнения (ОДУ) — это дифференциальное уравнение вида
![]()
где
![]() — неизвестная функция (возможно,
вектор-функция, тогда
— неизвестная функция (возможно,
вектор-функция, тогда
![]() ,
как правило, тоже вектор-функция со
значениями в пространстве той же
размерности; в этом случае говорят о
системе дифференциальных уравнений),
зависящая от независимой переменной
,
штрих означает дифференцирование по
.
Число
(порядок старшей производной, входящей
в данное уравнение) называется порядком
дифференциального уравнения (1).
,
как правило, тоже вектор-функция со
значениями в пространстве той же
размерности; в этом случае говорят о
системе дифференциальных уравнений),
зависящая от независимой переменной
,
штрих означает дифференцирование по
.
Число
(порядок старшей производной, входящей
в данное уравнение) называется порядком
дифференциального уравнения (1).
Наиболее часто встречаются дифференциальные уравнения вида
![]()
в
которых старшая производная
![]() выражается в виде функции от переменных
выражается в виде функции от переменных
![]()
![]() и производных
и производных
![]() порядков меньше
порядков меньше
![]() Такие дифференциальные уравнения
называются нормальными или разрешёнными
относительно производной.
Такие дифференциальные уравнения
называются нормальными или разрешёнными
относительно производной.
В противоположность уравнениям вида (2), дифференциальные уравнения вида (1) называются уравнениями, не разрешёнными относительно производной или неявными дифференциальными уравнениями.
Классическим решением дифференциального уравнения (2) называется раз дифференцируемая функция , удовлетворяющая уравнению во всех точках своей области определения. Обычно существует целое множество таких функций, и для выбора одного из них требуется наложить на него дополнительное условие. Начальным условием для уравнения (2) называется условие
![]()
где
![]() —
некоторое фиксированное значение
независимой переменной (фиксированный
момент времени), а
и
—
некоторое фиксированное значение
независимой переменной (фиксированный
момент времени), а
и
![]() — соответственно, фиксированные значения
функции
и всех её производных до порядка
— соответственно, фиксированные значения
функции
и всех её производных до порядка
![]() включительно. Дифференциальное уравнение
(2) вместе с начальным условием (3)
называется начальной задачей или задачей
Коши:
включительно. Дифференциальное уравнение
(2) вместе с начальным условием (3)
называется начальной задачей или задачей
Коши:
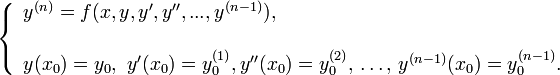
При достаточно общих ограничениях на функцию , стоящую в правой части уравнения (2), задача Коши для этого уравнение имеет единственное решение, определенное на некотором интервале оси времени , содержащем начальное значение (этот интервал, вообще говоря, может не совпадать со всей осью).
Основные задачи и результаты теории дифференциальных уравнений: существование и единственность решения различных задач для ОДУ, методы решения простейших ОДУ, качественное исследование решений ОДУ без нахождения их явного вида.
Пусть
в области
![]() рассматривается задача Коши:
рассматривается задача Коши:
![]()
где
![]() .
Пусть правая часть является непрерывной
функцией в
.
Пусть правая часть является непрерывной
функцией в
![]() .
В этих предположениях имеет место
теорема Пеано, устанавливающая локальную
разрешимость задачи Коши: Пусть a>0 и
b>0 таковы, что замкнутый прямоугольник
.
В этих предположениях имеет место
теорема Пеано, устанавливающая локальную
разрешимость задачи Коши: Пусть a>0 и
b>0 таковы, что замкнутый прямоугольник
![]()
принадлежит
области D, тогда на отрезке
![]() ,
где
,
где
![]() ,
,
![]() ,
существует решение задачи Коши.
,
существует решение задачи Коши.
Указанный
отрезок называется отрезком Пеано.
Заметим, что, локальный характер теоремы
Пеано не зависит от гладкости правой
части. Например, для
![]() и для
и для
![]() решение
решение
![]() существует лишь на интервале
существует лишь на интервале
![]() .
Также отметим, что без дополнительных
предположений относительно гладкости
правой части, нельзя гарантировать
единственность решения задачи Коши.
Например, для
.
Также отметим, что без дополнительных
предположений относительно гладкости
правой части, нельзя гарантировать
единственность решения задачи Коши.
Например, для
![]() возможно более одного решения.
возможно более одного решения.
Чтобы сформулировать теорему о единственности решения задачи Коши, необходимо наложить дополнительные ограничения на правую часть. Будем говорить, что функция f(x,y) удоволетворяет условию Липшица на D относительно y, если существует постоянная L такая, что
![]()
для
всех
![]() ,
i=1,2.
,
i=1,2.
Пусть правая часть f(x,y) дополнительно удовлетворяет условию Липшица на D относительно y, тогда задача Коши не может иметь в D более одного решения.
Также отметим, что хотя эта теорема имеет глобальный характер, тем не менее она не устанавливает существование глобального решения.
Для существования глобального решения необходимо наложить условия на рост правой части по y: пусть функция f удовлетворяет условию
![]()
где A>0 - константа не зависящая ни от x, ни от y, тогда задача Коши имеет решение в D. В частности, из этой теоремы следует, что задача Коши для линейных уравнений (с непрерывными по x коэффициентами) имеет глобальное решение.
Уравнения с разделенными переменными
P(x)dx+Q(y)dy=0
Общий интеграл
∫P(x)dx+∫Q(y)dy=C
Дифференциальное уравнение
![]() (3.1)
(3.1)
называется уравнением с разделяющимися переменными.
Умножая
обе части уравнения на
![]() , получаем уравнение
, получаем уравнение
(3.2)
В уравнении (3.2) коэффициент при dx зависит только от x, а коэффициент при dy зависит только от y. Значит, в уравнении (3.2) переменные разделены. Интегрируя, получаем:
![]()
![]() +
+
![]()
Линейное дифференциальное уравнение первого порядка с переменными коэффициентами имеет общий вид
![]()
Уравнения в такой форме могут быть решены путём умножения на интегрирующий множитель
![]()
получим
![]()
используем правило дифференцирования произведения
![]()
что, после интегрирования обеих частей, дает нам
![]()
![]()
Таким образом, решение линейного дифференциального уравнения первого порядка
![]()
(в частности, с постоянными коэффициентами) имеет вид
![]()
где
![]() является константой интегрирования.
является константой интегрирования.
Однородное уравнение второго порядка:
![]()
интегрируется следующим образом:
Пусть
![]() — корни характеристического уравнения.
— корни характеристического уравнения.
![]() ,
,
являющегося квадратным уравнением.
Вид
общего решения однородного уравнения
зависит от значения дискриминанта
![]() :
:
при
![]() уравнение имеет два различных вещественных
корня
уравнение имеет два различных вещественных
корня
![]()
Общее решение имеет вид:
![]()
при
![]() — два совпадающих вещественных корня
— два совпадающих вещественных корня
![]()
Общее решение имеет вид:
![]()
при
![]() существуют два комплексно сопряженных
корня
существуют два комплексно сопряженных
корня
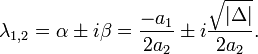
Общее решение имеет вид:
![]()
Если дано уравнение y'' = f(x), то его порядок можно понизить введением новой функции p(x), такой, что y' = p(x). В результате мы получим дифференциальное уравнение первого порядка
![]()
Решая его, находим функцию p(x). Затем решаем второе уравнение
![]()
получаем общее решение исходного уравнения.
Уравнение вида y''+ρy'+qy=f(x), где ρ и q – вещественные числа, f(x) – непрерывная функция, называется линейным дифференциальным уравнением с постоянными коэффициентами.
Рассмотрим линейное уравнение второго порядка вида:
y''+ρy'+qy=0, (1)
у которого правая часть f(x) равна нулю. Такое уравнение называется однородным.
Уравнение
K2+ρK+q=0 (2)
называется характеристическим уравнением данного уравнения (1).
Характеристическое уравнение (2) является квадратным уравнением, имеющим два корня. Обозначим их через К1 и К2.
Общее решение уравнения (1) может быть записано в зависимости от величины дискриминанта D=ρ2–4q уравнения (2) следующим образом:
1. При D>0 корни
характеристического уравнения
вещественные и различные (К1≠К2), и общее
решение имеет вид
![]() .
.
2. При D=0 корни
характеристического уравнения
вещественные и равные (К1=К2=К), и общее
решение имеет вид:
![]()
3. Если D<0, то корни
характеристического уравнения
комплексные:
![]() ,
где
,
где
![]() – мнимая единица,
– мнимая единица,
![]() и общее решение (К1=α+βi, К2=α–βi, β≠0),
имеет вид y=eαx(C1 cosβx+C2 sinβx).
и общее решение (К1=α+βi, К2=α–βi, β≠0),
имеет вид y=eαx(C1 cosβx+C2 sinβx).
Функции y1(x), y2(x), ..., yn(x), определённые на отрезке [a;b], называются линейно зависимыми на [a;b] , если существуют постоянные α1, α2, ..., αn , не равные нулю одновременно и такие, что α1y1(x) + α2y2(x) + ... + αnyn(x) = 0 для всех x из отрезка [a;b].
В противном случае функции y1(x), y2(x), ..., yn(x) называются линейно независимыми.
Линейную зависимость и линейную независимость функций определяют также на (a;b) , (a;b] , [a;b) , на бесконечных промежутках.
Справедливо следующее утверждение.
Функции y1(x), y2(x), ..., yn(x) линейно зависимы на отрезке [a;b] тогда и только тогда, когда хотя бы одна из них является линейной комбинацией других на этом отрезке .
Справедливо следующее утверждение.
Функции y1(x), y2(x), ..., yn(x) линейно зависимы на отрезке [a;b] тогда и только тогда, когда хотя бы одна из них является на этом отрезке линейной комбинацией других .
Очевидны следующие утверждения.
• Если среди функций y1(x), y2(x), ..., yn(x) есть нулевая функция, то функции линейно зависимы.
• Если функции y1(x), y2(x), ..., yk(x) линейно зависимы, то при любых yk + 1(x), yk + 2(x), ..., yn (x) функции y1(x), y2(x), ..., yk(x), yk + 1(x), ..., yn(x) также линейно зависимы.
• Если функции y1(x), y2(x), ..., yn(x) линейно зависимы на отрезке [a;b] , то они линейно зависимы и на любом отрезке, лежащем внутри [a;b] .
• Если функции y1(x), y2(x), ..., yn(x) линейно независимы на [a;b] , то они линейно независимы и на любом отрезке, содержащем отрезок [а;b] (если, они определены на этом отрезке).
Вектор–функции Y1(x), Y2(x), ..., Yn(x),
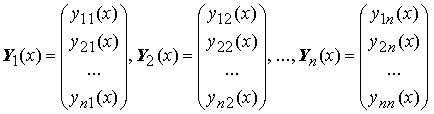
называются линейно зависимыми на отрезке [a;b] , если существуют постоянные α1, α2, ..., αn , не равные нулю одновременно и такие, что
α1 Y1(x) + α2 Y2(x) + ... + αn Yn(x) = 0
для всех x из отрезка [a; b].
В противном случае функции Y1(x), Y2(x), ..., Yn(x) называются линейно независимыми.
Вронскиа́н
(определитель Вронского) системы функций
![]() ,
дифференцируемых на промежутке
,
дифференцируемых на промежутке
![]() (n-1)-раз — функция на
,
задаваемая определителем следующей
матрицы:
(n-1)-раз — функция на
,
задаваемая определителем следующей
матрицы:
.

Также
вронскианом называют функцию, заданную
определителем более общего вида. А
именно, пусть задано n вектор-функций
![]() с n компонентами:
с n компонентами:
![]() .
Тогда определитель будет выглядеть так
(чтобы избежать разночтений обозначим
его
.
Тогда определитель будет выглядеть так
(чтобы избежать разночтений обозначим
его
![]() ):
):
.

Определитель Вронского применяется для решения дифференциальных уравнений, например для того, чтобы узнать, являются ли найденные решения однородного линейного дифференциального уравнения (либо системы уравнений) линейно независимыми. Это помогает в поиске его общего решения.
Теорема. Если
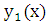 и
и
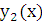 – линейно независимые решения уравнения
(2.3), то их линейная комбинация
– линейно независимые решения уравнения
(2.3), то их линейная комбинация
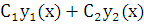 ,
где
,
где
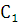 и
и
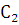 – произвольные постоянные, будет общим
решением этого уравнения.
– произвольные постоянные, будет общим
решением этого уравнения.
Теорема (о ФСР).
Пусть ранг основной
матрицы
![]() ,
где
— число переменных системы (1), тогда:
,
где
— число переменных системы (1), тогда:
ФСР (1) существует:
![]()
она состоит из
![]() векторов;
векторов;
общее решение системы
имеет вид
![]() .
.
Замечание:
Если
![]() ,
то ФСР не существует.
,
то ФСР не существует.
Линейное дифференциальное уравнение с постоянными коэффициентами — обыкновенное дифференциальное уравнение вида:
![]()
где
![]() —
искомая функция,
—
искомая функция,
![]() — её
— её
![]() -тая
производная,
-тая
производная,
![]() — фиксированные числа,
— фиксированные числа,
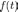 —
заданная функция (когда
—
заданная функция (когда
![]() ,
имеем линейное однородное уравнение,
иначе — линейное неоднородное уравнение).
,
имеем линейное однородное уравнение,
иначе — линейное неоднородное уравнение).
Рассмотрим ЛНДУ второго порядка с постоянными коэффициентами, т. е. уравнение
![]()
где р и q - некоторые числа.
Согласно
теореме 5.1, общее решение уравнения
(5.10) представляет собой сумму общего
решения
![]() соответствующего однородного уравнения
и частного решения у* неоднородного
уравнения. Частное решение уравнения
(5.10) может быть найдено методом вариации
произвольных постоянных (п. 5.2).
соответствующего однородного уравнения
и частного решения у* неоднородного
уравнения. Частное решение уравнения
(5.10) может быть найдено методом вариации
произвольных постоянных (п. 5.2).
Для уравнений с постоянными коэффициентами (5.10) существует более простой способ нахождения у*, если правая часть ƒ(х) уравнения (5.10) имеет так называемый «специальный вид»:
I.
![]() или
или
II.
![]()
Суть метода, называемого методом неопределенных коэффициентов, состоит в следующем: по виду правой части ƒ(х) уравнения (5.10) записывают ожидаемую форму частного решения с неопределенными коэффициентами, затем подставляют ее в уравнение (5.10) и из полученного тождества находят значения коэффициентов.
Рассмотрим линейное неоднородное дифференциальное уравнение
y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = f(x).
Общим решением этого уравнения на отрезке [a;b] называется функция y = Φ(x, C1,..., Cn ), зависящая от n произвольных постоянных C1,..., Cn и удовлетворяющая следующим условиям :
− при любых допустимых значениях постоянных C1,..., Cn функция y = Φ(x, C1,..., Cn ) является решением уравнения на [a; b] ;
− какова бы ни была начальная точка (x0, y0, y1,0 ,..., yn − 1,0 ) , x0∈ [a;b] , существуют такие значения C1 =C10 , ..., Cn = Cn0 , что функция y = Φ(x, C10 , ..., Cn0) удовлетворяет начальным условиям y(x0) = y0, y '(x0) = y1,0 ,..., y(n − 1) (x0) = yn− 1,0 .
Справедливо следующее утверждение ( теорема о структуре общего решения линейного неоднородного уравнения).
Если все коэффициенты уравнения линейного однородного дифференциального уравнениния непрерывны на отрезке [a;b] , а функции y1(x), y2(x),..., yn(x) образуют фундаментальную систему решений соответствующего однородного уравнения, то общее решение неоднородного уравнения имеет вид
y(x,C1,..., Cn) = C1 y1(x) + C2 y2(x) + ... + Cn yn(x) + y*(x),
где C1,...,Cn — произвольные постоянные, y*(x) — частное решение неоднородного уравнения.
В 41
