- •16. Типы конечных графов
- •Типы конечных графов
- •Матрицы смежности и инцидентности
- •Изоморфизм графов общего вида
- •Признаки непланарных графов
- •Алгоритм поиска в глубину
- •Реализация
- •Способы построения матрицы достижимости [править]Перемножение матриц
- •[Править]Случай нескольких путей
- •Каркас неориентированного графа
- •Формулировка
- •[Править]Оценка
- •Обозначения
- •[Править]Псевдокод
- •[Править]Описание
- •[Править]Доказательство корректности
- •Неформальное описание
- •[Править]Формальное описание
- •Основные определения
- •Классификация автоматов по логическим свойствам функций переходов и выходов
- •[Править]Автомат Мили
- •[Править]Автомат Мура
- •Форма компактного представления, применяемая во время выполнения
- •Реализация компактного представления
- •Анализ конечных автоматов.
- •Описание
- •Алгоритм симплекс-метода [править]Усиленная постановка задачи
- •[Править]Алгоритм
- •Модели вычислений
- •Описание
- •Устройство машины Тьюринга
- •[Править]Описание машины Тьюринга
- •Условия применимости
- •[Править]Принцип жадного выбора
- •[Править]Оптимальность для подзадач
16. Типы конечных графов
Если
граф не имеет ребер (т.е. ![]() ),
то все его вершины изолированы, и он
называетсяпустым или нульграфом.
),
то все его вершины изолированы, и он
называетсяпустым или нульграфом.
Простой
неориентированный граф, в котором любые
две вершины соединены ребром,
называется полным.
Полный граф с ![]() вершинами
обозначают символом
вершинами
обозначают символом ![]() (рис.4.2,
граф
(рис.4.2,
граф ![]() ).
Граф порядка n без
ребер называется пустым и
обозначается
).
Граф порядка n без
ребер называется пустым и
обозначается ![]() .
Граф
.
Граф ![]() называется
тривиальным. Можно
расширить полный граф до полного
графа с петлями,
добавляя петлю в каждой вершине (рис.4.6).
В ориентированном полном графе
имеются пары ребер, по одному в каждом
направлении, соединяющие любые две
различные вершины.
называется
тривиальным. Можно
расширить полный граф до полного
графа с петлями,
добавляя петлю в каждой вершине (рис.4.6).
В ориентированном полном графе
имеются пары ребер, по одному в каждом
направлении, соединяющие любые две
различные вершины.
Турниром называется орграф, любую пару вершин которого соединяет только одна дуга. Турнир отличается от полного ориентированного графа тем, что у него нет противоположно направленных дуг.
Граф
называется однородным (регулярным)
степени ![]() ,
если степени всех его вершин одинаковые
и равны
.
Однородный граф степени 1
называется паросочетанием.
Примерами однородных графов могут
служить графы, образованные вершинами
и ребрами пяти первых правильных
многогранников (или, так их
называют, платоновых тел):
тетраэдра и куба (степени 3), октаэдра
(степени 4), додекаэдра (степени 3),
икосаэдра (степени 5). Граф третьей
степени называют кубическим,
он обладает рядом интересных свойств
и, в частности, всегда имеет четное число
вершин. Три кубических графа изображены
на рис.4.2.
,
если степени всех его вершин одинаковые
и равны
.
Однородный граф степени 1
называется паросочетанием.
Примерами однородных графов могут
служить графы, образованные вершинами
и ребрами пяти первых правильных
многогранников (или, так их
называют, платоновых тел):
тетраэдра и куба (степени 3), октаэдра
(степени 4), додекаэдра (степени 3),
икосаэдра (степени 5). Граф третьей
степени называют кубическим,
он обладает рядом интересных свойств
и, в частности, всегда имеет четное число
вершин. Три кубических графа изображены
на рис.4.2.
Из
выписанной выше формулы, связывающей
число звеньев графа ![]() со
степенями его вершин, для случая
однородного графа степени
(все
со
степенями его вершин, для случая
однородного графа степени
(все ![]() ),
получим:
),
получим:
![]() .
.
Напоминаем,
что ![]() число
вершин графа. Поэтому, если
нечетное
число, то
должно
быть четным, и, следовательно, у любого
однородного графа нечетной степени (и
кубического тоже) всегда четное количество
вершин.
число
вершин графа. Поэтому, если
нечетное
число, то
должно
быть четным, и, следовательно, у любого
однородного графа нечетной степени (и
кубического тоже) всегда четное количество
вершин.
Орграф
называется однородным
степени
,
если полустепени всех его вершин
одинаковые и равны
: ![]() =
=![]() =
.
В этом случае
=
.
В этом случае
![]() .
.
Здесь, как и раньше, и число вершин и дуг графа.
Если
множество вершин простого графа ![]() можно
разбить на два непересекающихся
подмножества (доли)
можно
разбить на два непересекающихся
подмножества (доли) ![]() ,
, ![]() (
(![]() )
и при этом не существует ребер, соединяющих
вершины одного и того же подмножества,
то такой граф называется двудольным (иначе биграфом).
Полный двудольный (у него каждая вершина
из
соединена
с каждой вершиной из
).
обозначают символом
)
и при этом не существует ребер, соединяющих
вершины одного и того же подмножества,
то такой граф называется двудольным (иначе биграфом).
Полный двудольный (у него каждая вершина
из
соединена
с каждой вершиной из
).
обозначают символом ![]() где
где ![]() ,
, ![]() .
.
Типы конечных графов
Если множество вершин графа конечно, то он называется конечным графом. Для ориентированного ребра (дуги) различают начальную вершину, из которой дуга исходит, и конечную вершину, в которую дуга заходит. Ребро, граничными вершинами которого является одна и та же вершина, называется петлей. Ребра с одинаковыми граничными вершинами являются параллельными и называются кратными. В общем случае граф может содержать и изолированные вершины, которые не являются концами ребер и не связаны ни между собой, ни с другими вершинами.
Матрицы смежности и инцидентности
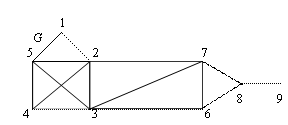
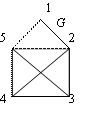
На
рис 3.12 изображено множество точек V и
множество линий E,
соединяющих эти точки, которые все
вместе образуют граф
Г.
Если линии имеют стрелки, то граф
называется ориентированным или орграфом
Г0 (рис.
3.13). Внутренних различий между Г и Г0 гораздо
меньше, чем между графом,
изображающим правильную решетку
из подгрупп для какой-нибудь группы,
например,S( ![]() )
(рис. 2.18), и графом, изображающим сильно
неправильную метарешетку M16 (рис.
2.26).
)
(рис. 2.18), и графом, изображающим сильно
неправильную метарешетку M16 (рис.
2.26).
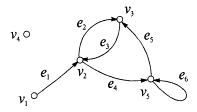
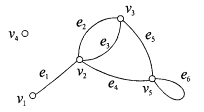
Рис. 3.12 Рис. 3.13
Внешняя морфология графа (со стрелками или без них) играет подчиненную роль, математическая же сущность представленного графом объекта всегда остается где-то за рамками рисунка. Изображение графа в большинстве случаев является проекцией или тенью этой сущности и самостоятельного значения не имеет. Однако морфология расположения точек и линий, тем не менее, поддается определенной математической классификации и описанию. Этим мы намерены заняться в этом и последующем подразделах.
Линии в графе Г здесь и далее будем называть ребрами, а ориентированные линии в орграфе Г0 — дугами. О вершинах и ребрах (дугах) говорят, что они инцидентны, если вершина принадлежит ребру (дуге); если вершина не инцидентна никакому ребру (дуге), то она называется изолированной (v4). Путь называется простым, если никакая дуга или ребро не встречается в нем дважды. Путь называется элементарным, если никакая вершина в нем не встречается дважды.
Цикл — это замкнутый путь в неориентированном графе. Контур — это ориентированный цикл в орграфе. Понятия простоты и элементарности распространяются на циклы и контуры. Контур или цикл, который содержит все ребра или дуги графа, называется эйлеровым. Можно показать, что связанный орграф (т.е. без изолированных фрагментов) содержит эйлеров контур тогда и только тогда, когда для каждой вершины число входящих дуг равно числу выходящих; связанный неориентированный граф содержит эйлеров цикл тогда и только тогда, когда степень каждой вершины четна. Степенью (валентностью) вершины называется число инцидентных ей ребер. Простой путь, который проходит через все вершины графа, называется гамильтоновым. Если в простом графе с n вершинами степень каждой вершины не меньше n/2, то такой граф обязательно будет гамильтоновым. Однако легко построить гамильтонов граф, у которого степень вершины меньше n/2.
Графы Г и Г0 можно представить в аналитической форме либо матрицей смежности A, либо матрицей инцидентности B. Для нашего конкретного неориентированного графа Г матрицы A и B выглядят следующим образом:
|
|
A(Г) = |
B(Г) = |
Матрица смежности для неориентированного графа всегда симметрична. Фигурирующая в ней 2 может быть в некоторых случаях заменена на 1. В матрице инцидентности сумма единиц по столбцам указывает на степень вершины vi. Нередко расположение вершин и ребер в этой матрице меняют местами (транспонируют). Так, для нашего конкретного орграфа Г0 матрица A и B выглядят иначе:
|
|
A(Г0 ) = |
B(Г0 ) = |
В общем случае матрица смежности для ориентированного графа уже не будет симметричной. В матрице инцидентности ставится 1, если дуга исходит из вершины, и – 1, если дуга заходит в нее.
Число дуг в пути минимальной длины от вершины vi до vj называется расстоянием r(vi, vj). Если между вершинами не существует никакого пути, то расстояние равно бесконечноти: r(vi, vj) = ∞.
Для вершины vi можно определить среднее отклонение от центра графа:
![]()
где m — число дуг в графе Г , v – пробегает вершины V графа Г.
Вершина v0, для которой эта сумма окажется минимальной, называется центром графа Г. В роли центра могут выступать несколько вершин. Для пересчета возможных путей длины r, рассмотрим различные степени матрицы смежности A(Г0). Пусть дан орграф Г0 (рис. 3.14).
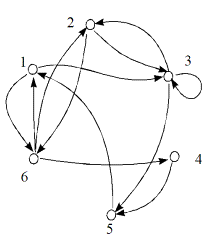
Рис. 3.14
A(Г0)
=  ,
R = r(i, j)
=
,
R = r(i, j)
=  .
.
Общее число дуг m = 12; матрица R = r(i, j) отражает расстояние между вершинами; на ее основе рассчитываем всевозможные отклонения: D(1) = D(2) = D(6) = 2/3 — центр графа Г0, который состоит из трех вершин 1, 2 и 6; остальные отклонения равны: D(3) = 3/4, D(4) = 13/12, D(5) = 11/12.
17. Эйлеровы графы |
|
Определение 1 |
Цикл называется эйлеровым, если он содержит все ребра графа. Цепь называется эйлеровой, если она содержит все ребра графа. |
Определение 2 |
Граф называется эйлеровым, если в нем найдется эйлеров цикл. Пример Граф “Сабли Магомета” является эйлеровым, так как в нем есть эйлеров цикл 123475287651.
Теорема 3 (Эйлера) Связный граф является эйлеровым тогда и только тогда, когда он не содержит вершин нечетной степени. Доказательство Достаточность. Покажем,
что если в графе все вершины четной
степени, то он эйлеров. Выберем
произвольную вершину графа Заметим,
что если мы попали в какую-либо вершину
(не важно в какой раз) всегда сможем
из нее выйти, т.к. ее степень четная. С
учетом того, что вершин конечное
число, на
каком-то шаге мы вернемся в
.
Если при этом все ребра графа уже
закрашены, то получившийся цикл и
является эйлеровым. Иначе выбираем
произвольную вершину Если
еще не все ребра графа закрашены, то
аналогичным образом выбираем вершину Так как число ребер графа конечно, то на каком-то шаге все ребра графа окажутся закрашенными. К этому моменту граф будет представлять собой объединение некоторого числа окрашенных разными цветами циклов. Покажем методом математической индукции по числу полученных циклов, что из них можно составить эйлеров цикл. Базис индукции. Пусть,
закрасив все ребра указанным методом,
получили два цикла. Объединим эти
циклы: из вершины Педположение индукции. Пусть после k описанных выше процедур все ребра графа окрашены. Допустим, что объединение k полученных циклов, есть эйлеров цикл Индуктивный переход. Пусть после k+1 описанной выше процедуры все ребра графа окрашены. Докажем, объединение k+1 полученного цикла, есть эйлеров цикл. Объединив любые k циклов в один, мы приходим к задаче объединения в эйлеров цикл двух циклов, которая описана в базе индукций. Необходимость. Пусть дан эйлеров граф. Покажем, что все его вершины имеют четную степень. Так как граф эйлеров, то в нем найдется эйлеров цикл, содержащий все ребра, а значит, все вершины графа. Если в данном эйлеровом цикле некоторая вершина встретилась k раз, то число инцидентных ей ребер равно 2k, а значит, ее степень равна 2k. |
Определение 3 |
Цепь, содержащая все ребра графа, называется эйлеровой. |
Определение 4 |
Граф, обладающий эйлеровой цепью, называется квазиэйлеровым. Теорема 5
Граф является квазиэйлеровым, если в нем не более двух вершин нечетной степени.
Доказательство
Очевидно, что никакая вершина нечетной степени не может принадлежать эйлеровой цепи, если только она не является его концом. Так как эйлерова цепь в графе имеет только два конца, то вершин нечетной степени в квазиэйлеровом графе не может быть больше двух. А так как в графе число вершин нечетной степени четно, то одной вершины нечетной степени тоже быть не может. Если их нуль, то граф будет эйлеровым. Значит, в квазиэйлеровом графе может быть только две вершины нечетной степени.
Замечание
В квазиэйлеровом графе существующие у него две вершины нечетной степени всегда будут являться концами любой эйлеровой цепи.
П
Граф G является квазиэйлеровым, так как, например, цепь 4,5,1,2,3,5,2,4,3 – эйлерова. В графе G ровно две вершины нечетной степени: 3 и 4.
Теорема 6 (о разложении произвольного графа на попарно реберно-непересекающиеся цепи)
Если в графе равно k вершин имеют нечетную степень, то его можно разложить на не менее чем k/2 попарно реберно-непересекающихся цепей.
Доказательство
Очевидно, что граф можно разложить на попарно реберно-непересекающиеся цепи, взяв, например, в качестве каждой такой цепи по одному разному ребру графа. Покажем, что реберно-непересекающихся цепей не может быть меньше, чем k/2. Заметим, что вершины нечетной степени графа должны обязательно быть концами каких-то из этих цепей. Значит минимальное число вершин, являющихся концами цепей равно k, соответственно минимальное количество цепей равно k/2.
Пример
В графе G шесть вершин нечетной степени: 2,3,4,6,8,9. Поэтому, его можно разложить на три попарно реберно-непересекающиеся цепи, концами которых являются перечисленные вершины нечетной степени. Например, 2,1,5,4,2,5,3,4; 3,2,7,6,8; 9,8,7,3,6. |
-------Гамильтоновы графы |
|
Определение 1 |
Цикл называется гамильтоновым, если он проходит через каждую вершину графа (за исключением крайней) в точности один раз. Цепь называется гамильтоновой, если она проходит через каждую вершину графа в точности один раз. Замечание Гамильтонов цикл и гамильтонова цепь всегда являются простыми. Они могут не содержать всех ребер графа. |
Определение 2 |
Граф называется гамильтоновым, если он обладает гамильтоновым циклом. |
Определение 3 |
Граф называется квазигамильтоновым, если он обладает гамильтоновой цепью. Пример
Граф G является квазигамильтоновым, и не является гамильтоновым. 2,4,3,1,5 – гамильтонова цепь.
|
|
18. Изоморфизм графов
В теории
графов изоморфизмом
графов ![]() и
и ![]() называется биекция между
множествами вершин графов
называется биекция между
множествами вершин графов ![]() такая,
что любые две вершины
такая,
что любые две вершины ![]() и
и ![]() графа
графа ![]() смежны,
если и только если вершины
смежны,
если и только если вершины ![]() и
и ![]() смежны
в графе
смежны
в графе ![]() .
Здесь графы понимаются неориентированными
и не имеющими весов вершин и ребер. В
случае, если понятие изоморфизма
применяется к ориентированным или
взвешенным графам, накладываются
дополнительные ограничения на сохранение
ориентации дуг и значений весов. Если
изоморфизм графов установлен, они
называются изоморфными и обозначаются
как
.
Здесь графы понимаются неориентированными
и не имеющими весов вершин и ребер. В
случае, если понятие изоморфизма
применяется к ориентированным или
взвешенным графам, накладываются
дополнительные ограничения на сохранение
ориентации дуг и значений весов. Если
изоморфизм графов установлен, они
называются изоморфными и обозначаются
как ![]() .
.
Иногда
биекция ![]() записывается
в виде подстановки изоморфизма
записывается
в виде подстановки изоморфизма ![]() .
Некоторые задачи обработки графов
требуют не только проверки изоморфизма,
но и выяснения его подстановки.
.
Некоторые задачи обработки графов
требуют не только проверки изоморфизма,
но и выяснения его подстановки.
Отношение
изоморфизма графов представляет
собой отношение
эквивалентности,
определенное для графов, и позволяет
произвести разбиение исходного класса всех
графов наклассы
эквивалентности.
Множество графов, изоморфных друг другу,
называется классом
изоморфизма графов (англ.),
их число в зависимости от ![]() представляет
собой последовательность A000088 в OEIS (1,
1, 2, 4, 11, 34, 156, 1044, 12346, ...).
представляет
собой последовательность A000088 в OEIS (1,
1, 2, 4, 11, 34, 156, 1044, 12346, ...).
В случае, если биекция отображает граф сам на себя (графы и совпадают), она называется автоморфизмом графа .


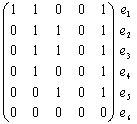



 ример
ример