
- •1. Общие положения к типовому заданию.
- •Способ подстановки
- •3. Уравнения, допускающие понижение порядка.
- •6. Системы линейных дифференциальных уравнении с постоянными коэффициентами
- •6.I. Теоретические вопросы
- •3. Найти общее решение уравнения:
- •4. Уравнения, интегрируемые понижением порядка. Найти частные решения:
- •Задачи, связанные с составлением дифференциального уравнения……………………………………………………………... 3
1. Общие положения к типовому заданию.
Математические методы все шире и шире проникают в повседневную инженерную деятельность, в приложения математики к технике особое место занимают дифференциальные уравнения. В своей практической работе инженер (конструктор, механик, технолог) часто сталкивается с необходимостью решения задач с переменными величинами, самостоятельного составления дифференциальных уравнений.
Предлагаемое типовое задание посвящено изучению темы "Обыкновенные дифференциальные уравнения". Цель его - помочь студенту усвоить данный раздел и приобрести навыки самостоятельной работа.
Каждый вариант типового задания содержит шесть пунктов:
Теоретический вопрос
Задачу, связанную с выводом какого-то дифференциального уравнения
и его решением.
Уравнение первого порядка (определение типа уравнения и его интегрирования).
Уравнение, допускающее понижение порядка.
Линейные дифференциальные уравнения с постоянными коэффициентами.
Систему линейных дифференциальных уравнений с постоянными коэффициентами.
Пункт 5 в каждом варианте содержит три уравнения 51-3, из которых 51-2 посвящены методу неопределенных коэффициентов, а 53 - методу вариации произвольных постоянных. Ниже приведены примеры решения задач с некоторыми методическими указаниями.
2. Задачи, связанные с составлением дифференциального уравнения.
Задача 1. Стальная проволока длиной Lо к с поперечным сечением S растягивается силой, постепенно возраставшей до величины P.
Найти работу растяжения
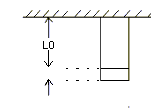
Решение: Рассматривая достаточно малые деформации, воспользуемся законом Гука согласно которому деформации пропорциональны напряжениям.
![]() (1)
(1)
При приращениях сил, мало отличающихся от нуля, приращение функции ∆L становится близким к значению дифференциала dl, т.е. при ∆Р = dP→ 0, ∆l ≈ dl. Тогда соотношение (1) для элементарного акта растяжения запишем как:
![]() (2)
(2)
Работа растяжения на элементарном отрезке dl равна da = pdl
Здесь полагается, что на каждом элементарном отрезке работа совершается постоянной силой.
Вместо dl в формулу (3) подставим выражение из (2), тогда
![]() (4)
(4)
Интегрируя
(4), получим
![]()
![]() ,
где
С – постоянная интегрирования, равная
нулю по условию Ф=0 при з=0. Следовательно,
работа растяжения проволоки может быть
подсчитана по формуле:
,
где
С – постоянная интегрирования, равная
нулю по условию Ф=0 при з=0. Следовательно,
работа растяжения проволоки может быть
подсчитана по формуле:
![]()
Задача 2. Найти кривую, у которой абсцисса центра тяжести плоской фигуры, ограниченной осями координат этой кривой и ординатой любой её точки, равна ¾ абсциссы этой точки.
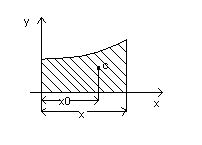
Решение: Абсцисс ацентра тяжести криволинейной трапеции, ограниченной сверху y = f(x) снизу осью OX, слева x=a,
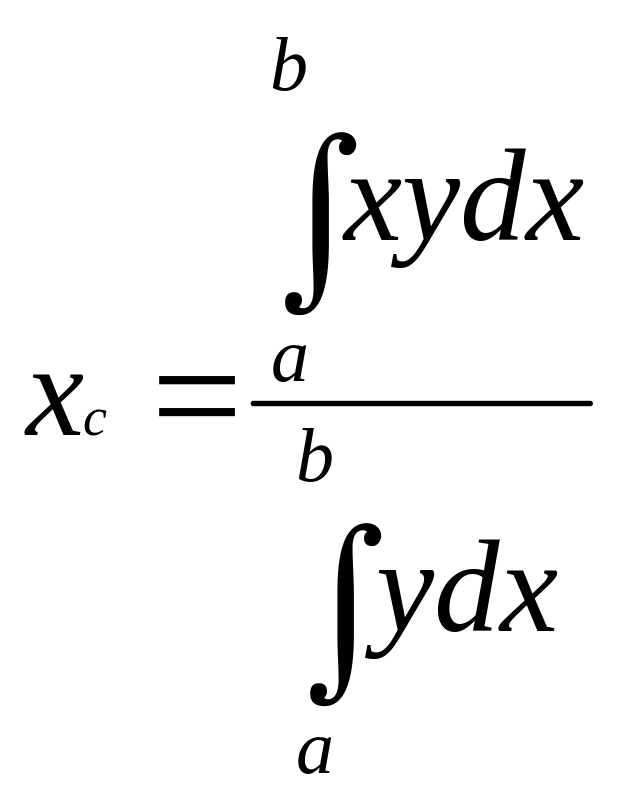 (1)
(1)
Применительно к рассматриваемой задаче, формулу (1) запишем в виде
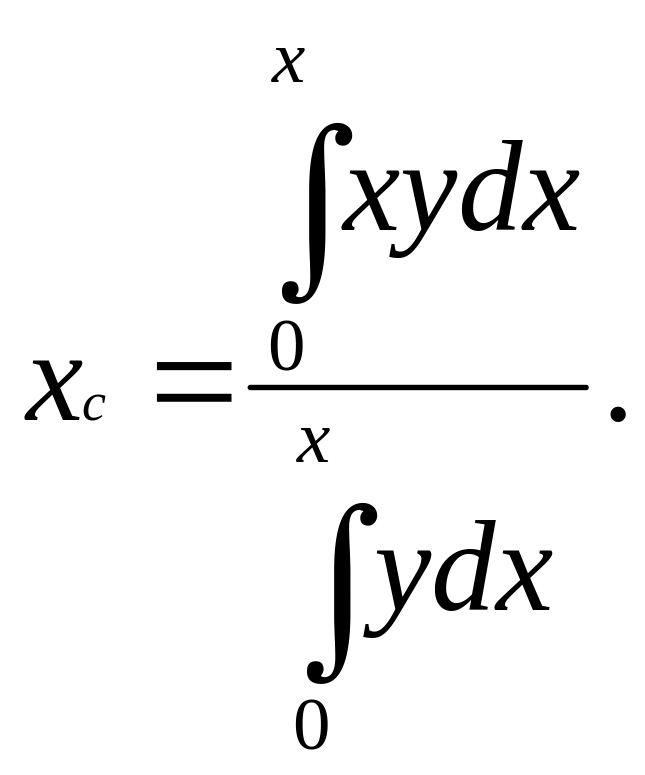 (2)
(2)
где xc = ¾ по условию. На основании (2) имеем интегральное уравнение
![]() (3)
(3)
Продифференцировав уравнение (3) по переменному верхнему пределу, получим
![]()
Продифференцируем полученное выражение вторично:
![]() (4)
(4)
Таким образом получим дифференциальное уравнение первого порядка с разделяющимися переменными, удовлетворяющее условиям задачи. Проинтегрируем уравнение (4)
![]()
откуда y = c*x2 , где с – произвольная постоянная. Следовательно, условию задачи удовлетворяет семейство парабол, проходящих через начало координат.
2. Уравнения первого порядка (определение типа уравнения и его интегрирование)
Задача 3. Найти общее и частное решение дифференциального уравнения
Y'+y*cosx = limx * cosx , удовлетворяющее начальным условиям
![]() Решение:
Это линейное дифференциальное уравнение
первого порядка, так как искомая
функция и её производная входят в
уравнение в первой степени и не
перемножаются, т.е. уравнение можно
представить в виде y'+p(x)y=Q(x).
Решение:
Это линейное дифференциальное уравнение
первого порядка, так как искомая
функция и её производная входят в
уравнение в первой степени и не
перемножаются, т.е. уравнение можно
представить в виде y'+p(x)y=Q(x).
Линейное уравнение можно интегрировать или способом вариации произвольной постоянной, или подстановкой Бернулли. Расcмотрим каждый из них.
Способ вариации произвольной постоянной.
Найдем
сначала общее решение линейного
однородного уравнения, соответствующее
данному неоднородному:
![]() .
В
этом yравнении
переменные разделяются:
.
В
этом yравнении
переменные разделяются:
![]()
Интегрируя,
получим
![]() или
или
![]()
Мы нашли общее решение линейного однородного уравнения. Общее решение неоднородного уравнения будем искать в том же виде, в каком мы получили общее решение соответствующего линейного уравнения, только производную С будем считать функцией от x (применим вариации постоянной), т.е. будем искать решение неоднородного уравнения в виде.
Y=cosl-sinx. Дифференцируя левую и праву части, получим:
![]() .
Полученные значения y
и y'
подставляем в заданное уравнение
.
Полученные значения y
и y'
подставляем в заданное уравнение
![]() будем иметь:
будем иметь:
![]()
Отсюда получаем:
![]()
Интегрируем:
![]()
Интеграл в первой части берем по частям:
![]()
![]()
Следовательно,
![]()
Таким
образом, если
![]() , то функция
, то функция
![]() является общим решениям данного
неоднородного линейного дифференциального
уравнения. Значит, общее решение данного
уравнения будет
является общим решениям данного
неоднородного линейного дифференциального
уравнения. Значит, общее решение данного
уравнения будет
![]() или
или
![]()
Найдем теперь искомое частное решение. Подставляя э полученное общее решение начальные условия у =0 при x=0, будем иметь.
![]() или
или
![]()
Частное
решение имеет вид
![]()
