Способ подстановки

Будем искать общее решение данного линейного уравнения в виде про­изведения двух функций

Продифференцируем . Подставляя эти значения у и y' в данное уравнение , будем иметь:

(*)

Так как решение уравнения ищем в виде произведения двух функций, то одну из них мы можем выбрать по своему усмотрение, поэтому потребу­ем, чтобы функция V обращала в нуль стоящее в скобках равенство (*), т.е. найдем какое-нибудь частное решение или Интегрируя, найдем

или

Замечание. Здесь мы не выписываем производную постоянную, т.к. нам нужно в качестве V иметь какую-нибудь функцию ( наиболее простую ), обращаете в ноль выражение в скобках (*). Подставляем в (*) подученное значение для V, будем иметь:

Разделяем переменные

Интегрируем

Таким образом, общее решение будет

Учитывая начальные условия, получим частное решение:

3. Уравнения, допускающие понижение порядка.

Задача 4. Найти частное решение дифференциального уравнения удовлетворяющее начальным условиям (1) , .

Решение: Данное уравнение допускает понижение порядка, так как в него не входит в явной виде y. Произведем понижение порядка.

Положим , тогда . Подставив эти значения у' и у'' в данное уравнение, получим которое является уравне­нием с разделяющимися переменными. Разделяем переменные

Производим интегрирование:

Ho p= у', поэтому (1), откуда (2) - это общее решение данного дифференциального уравнения. Найдем частное решение. Так как при x = 0 , то, подставляя эти значения в (1), найдем

Условие y=1 при x=0 подставляем в (2) (1) = с₂. Таким образом, из начальных условий вытекает, что C₁ = 3, С₂ = (1) и искомое частное решение имеет вид:

Задача 5. Проинтегрировать дифференциальное уравнение.

Решение. Данное уравнение не содержит в явном виде x , поэ­тому оно допускает понижение порядка. Положим: , тогда

.

При отыскании мы примем во внимание, что Р есть функция от Y. Подставляя полученные значения для и в данное уравне­ние, будем иметь: . После сокращения на р (если p = 0, то у=С - это одно из решений дан­ного уравнения) мы получим уравнение первого порядка с разделяющимися переменными (здесь искомой функцией является p, а аргументом y). Разделяем переменные: Выполняем интегрирование:

. Находим интеграл, стоящий в правой час­ти

.

Следовательно,

,

Но поэтому

Таким образом, есть общий интеграл данного диффе-ренциального уравнения.

5. Линейные дифференциальные уравнения с постоян­ными коэффициентами

Задача 6. Найти общее решение уравнения

(1)

Решение. Составим характеристическое уравнение: ;

его корни

Общим решением соответствующего однородного дифференциального урав­нения будет y=c₁+c₂sin2x+c₀cos2x. В правой части этого уравнения стоит сумма функций, поэтому частное решение неоднородного уравнения будем искать так: напишем два уравнения (2) и (3) и найдём частное реше­ние сначала для уравнения (2), обозначив его y₁, а затем для уравне­ния (3), обозначив его y₂, тогда частное решение искомого уравнения представится как . Правая часть неоднородного уравнения (2) имеет форму f₁(x)=4sin2x=l(0cos2x+4sin2x) т.е. в об­щем виде можно записать

Q_m(x)=4;

Комплексные числа , построенные по этой правой части, будут иметь вид и совпадут с корнями характеристического уравнения один раз, значит кратность R=I и поэтому частное решение надо искать по формуле , если n>m, r=1, l^ox=1

Дифферецируем:

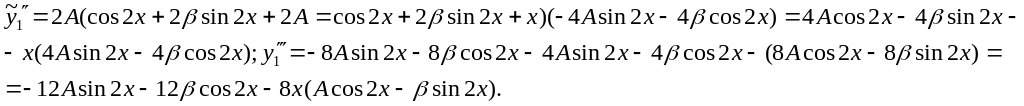
Подставляя значения и в данное неоднородное уравнение (2), получим тожво

или, делая приведение подобных членов,

Сравнивая коэффициенты в левой и правой частях тождества имеем:

-8A=4; ; следовательно: A=1/2, B=0.

Частное решение неоднородного линейного уравнения (2) будет

Аналогично найдем частное решение уравнения (3). Правая часть урав­нения (3) имеет форму , где , совпадает с корнам характеристического уравнения один раз, следовательно, кратность r = I. Частое решение неоднородного уравнения (3) будем искать в виде , для нашего случая

Дифференцируем:

Подставляя значения и в уравнение (3), получим тождество:

Сравнивая коэффициенты в левой и правой части тождества, имеем:

,

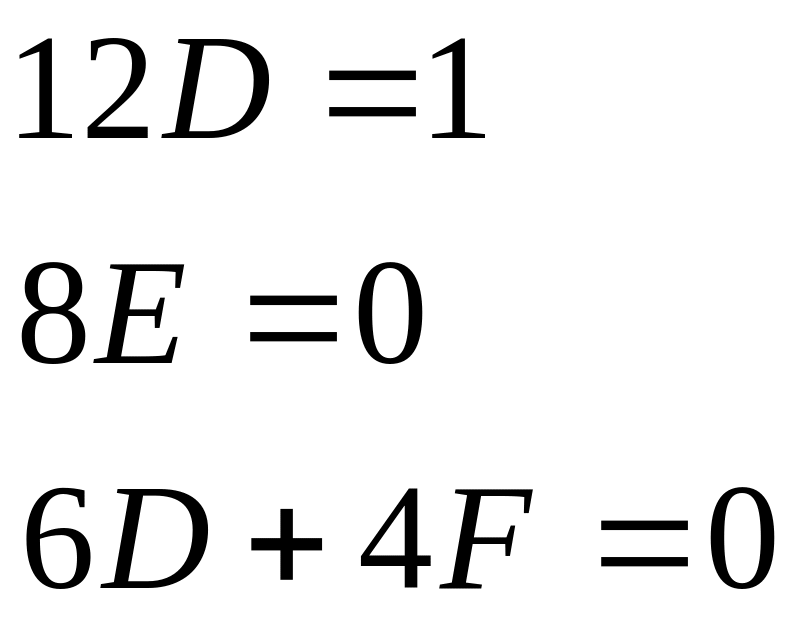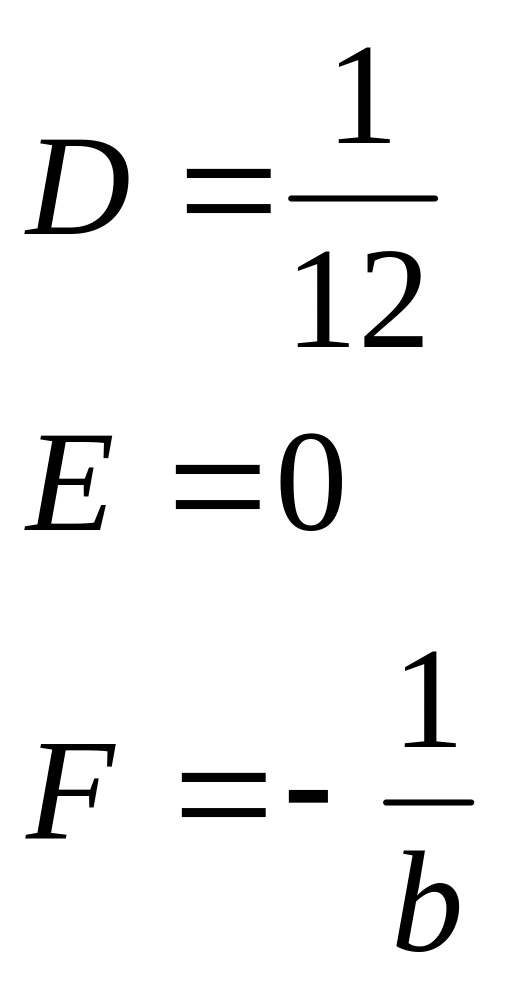
Тогда частное решение искомого уравнения (1) будет:

и общее решение имеет вид:

Задача 7. Найти вид общего решения

Решение. Характеристическое уравнение имеет корни . Значит, общее решение соответствующего однородного уравнения будет равно

Правая часть уравнения имеет форму f(x)=f₁(x)+f₂(x) , где

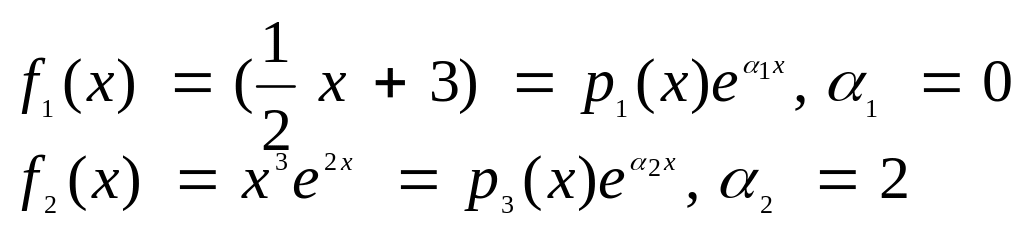
Частное решение , соответствующее правой части f₁(x), ищем в виде так как совпадает с корнем характеристического уравнения три раза. Получаем, что частное решение неод­нородного сравнения (3) имеет вид , совпадает с корнем характеристического уравнения два раза , а общее решение неоднородного уравнения

Задача 8. Найти решение уравнения удовлетворяющее начальным условиям

Решение. Составим характеристическое уравнение его корни равны соответственно . Следовательно, общим решением соответствующего однородного линейного уравнения будет:

Теперь ищем частное решение заданного неоднородного линейного диф­ференциального уравнения

Подставляем в заданное уравнение

или следовательно, А=-5 и Таким образом, общее решение данного уравнения будет

Так как

искомое решение

Задача 9. Найти общее решение .

Решение. Однородному уравнению соответствует характеристическое уравнение его корни Общим решением соответствующего однородного уравнения будет Подобрать частное решение неоднородного уравне­ния здесь нельзя, так как правая часть не специальная ( частное ре­шение можно подобрать в таком виде, в каком записана правая часть только тогда, когда последнее имеет вид Поэтому для отыскания частного решения данного дифференциального уравнения примем метод вариации произвольных постоянных, т.е. част­ное решение будем искать в виде , где y₁, y₂ - частное решение соответствующего линейного однородного уравнения, а функции u(x) и v(x) удовлетворяют следующей системе

а функция f(x) - это правая часть данного уравнения

Составив систему уравнении для отыскания u и v.

Тогда , .

Интегрируем .

Тогда частное решение уравнения будет равно

.

Общее решение

.