14.Гиперболические гомологии.

Гомологией называется нетождественное проективное преобразование плоскости, имеющее точечно неподвижную (инвариантную) прямую, называемую осью гомологии.

Свойства гомологии.

1. Прямая, проходящая через две несовпадающие соответственные точки,

преобразуется в себя (является неподвижной).

2. Прямые, проходящие через несовпадающие соответственные точки (не

принадлежащие одной прямой), проходят через одну неподвижную

(инвариантную) точку, называемую центром гомологии.

3. Прямая, не проходящая через центр гомологии, и ее образ пересекаются

на оси гомологии.

Гомология, центр которой не принадлежит оси, называется гиперболической.

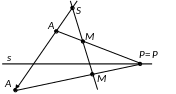
Гомология задается осью s, центром S и парой соответственных точек, лежащих на прямой, проходящей через центр. Обозначим такую гомологию (S, s; A, A).

Построение соответственных точек (фигур).

Пусть (S, s; A, A) – гомология, M – произвольная не двойная точка.

Найдем ее образ M= (M). Для этого последовательно проводим прямые 1) SM; 2) AM, AM  s = P (=P); 3) PA  M= AM  PA.

 – гиперболическая.

На расширенной плоскости выделяются частные виды гомологии.

1. Перспективно-аффинное (родственное) преобразование. Это гомология с несобственным центром. Среди них имеются

а) отражения со сжатием (или растяжением) к оси;

б) отражения – осевые симметрии (косая симметрия, симметрия);

в) сжатия к оси (либо растяжения);

г) параллельные переносы –  ( S_ , s_ , A, A);

д) сдвиги (перекосы) –  (S_ , s, (S_ s), A, A).

2. Гомотетия – (S, s_ , A, A); в частности это может быть центральная симметрия.

15. Линии 2-го порядка. Классификация.

Кривой второго порядка на проективной плоскости называется множество точек, координаты которых удовлетворяют уравнению

а₁₁х₁² + а₂₂ х₂² + a₃₃ х₃² + 2а₁₂ х₁х₂+ 2а₁₃ х₁х₃+ 2а₂₃ х₂х₃ = 0, где а₁₁, … , а₂₃ – действительные числа, не все из которых равны нулю.

В матричном виде: X^TAX = 0, A^T = A.

_{Примеры (классы) кривых второго порядка:}

1. х₁² + х₂² – х₃² = 0;( овальной кривой второго порядка)

2. х₁² – х₂² = 0;( пара прямых)

3. х₁² + х₂² = 0;( пара мнимых прямых)

4. х₁² = 0;( двойная прямая)

5. х₁² + х₂² + х₃² = 0 (мнимая кривая, мнимый овал)

Можно доказать, что любая кривая второго порядка в соответствующей системе координат имеет одно из пяти уравнений, и, значит, является одной из пяти вышеупомянутых кривых.

16. Пересечение линии 2-го порядка с прямой.

Пусть кривая второго порядка  задана уравнением а₁₁х₁² + а₂₂ х₂² + a₃₃ х₃² + 2а₁₂ х₁х₂+ 2а₁₃ х₁х₃+ 2а₂₃ х₂х₃ = 0 (1) и A(a_i ), B(b_i ) – две точки. Найдем пересечение прямой AB с кривой . Уравнение прямой AB : х_i = a_i + b_i.(1). Подставим (1) в (1 ):

;\s\do10(iа_ij (a_i + b_i)(a_j + b_j) _{= 0,}

²;\s\do10(iа_ij a_ia_j + 2;\s\do10(iа_ij a_ib_j + ²;\s\do10(iа_ij b_ib_j = 0, (2).

Это уравнение вида ² + 2 + ² = 0.(_*)

Возможны следующие случаи.

1.  =  =  = 0; тогда  и  любые, AB .

2.  =  = 0,   0; тогда  = 0 или  = 0 ; это значит AB   = {A, B}.

3.   0 или   0; пусть   0, тогда разделим (_*) на ²:

(/)² + 2(/) +  = 0; (3)

Это уравнение относительно неизвестного / имеет два корня (различные или совпадающие действительные, или комплексно-сопряженные). Подставляем ₁, ₁ и ₂, ₂ в (1) и получаем две точки пересечения (действительные или комплексные, а, может быть, совпадающие).

17.Касательные

Касательной к кривой 2 порядка  называется прямая, которая имеет с  одну (двойную) общую точку.

Пусть  задана уравнением а₁₁х₁² + а₂₂ х₂² + a₃₃ х₃² + 2а₁₂ х₁х₂+ 2а₁₃ х₁х₃+ 2а₂₃ х₂х₃ = 0 и A(a_i ) . Составим уравнение касательной l к  в точке A . Поскольку A  , то ;\s\do10(iа_ij a_ia_j= 0. Пусть B(b_i ) l . Тогда уравнение прямой AB: х_i = a_i + b_i . Пересечение AB с  находится из уравнения. Поскольку AB – касательная, то это уравнение должно свестись до ² = 0. С учетом остается потребовать ;\s\do10(iа_ij a_ib_j = 0. Это условие принадлежности B касательной l .Обозначим, как обычно, координаты B через x_i ; тогда уравнение касательной к  в точке A(a_i ).;\s\do10(i(а_ij a_i) x_j = 0 ,или (а₁₁а₁+ а₁₂a₂+ а₁₃a₃₎ х₁+ (а₁₂а₁₊ а₂₂а₂₊ а₂₃a₃₎х_{2 +} (а₁₃а₁₊ а₂₃а₂₊ а₃₃a₃₎ х₃= 0.

18. Полюс и поляра.

Пусть кривая 2 порядка  задана в плоскости ; ¯ уравнением а₁₁х₁² + а₂₂ х₂² + a₃₃ х₃² + 2а₁₂ х₁х₂+ 2а₁₃ х₁х₃+ 2а₂₃ х₂х₃ = 0 , и A(a_i ) – произвольная точка плоскости ; ¯ . Полярой точки A относительно  называется множество точек, координаты которых удовлетворяют уравнению ;\s\do10(i(а_ij a_i) x_j = 0  ;\s\do10( j =1u_j x_j = 0 (1), где мы обозначили u_j = ;\s\do10(i =1а_ij a_i. Мы видим, что поляра – это прямая (если не все u_j = 0). Точка A называется полюсом этой прямой.

Теорема о взаимности. Если точка B принадлежит поляре точки A, то A принадлежит поляре точки B.

Доказательство. Пусть кривая  имеет уравнение а₁₁х₁² + а₂₂ х₂² + a₃₃ х₃² + 2а₁₂ х₁х₂+ 2а₁₃ х₁х₃+ 2а₂₃ х₂х₃ = 0, а точки A и B – координаты a_i и b_i . Пусть p(A) и p(B) – поляры точек A и B. Уравнение p(A): ;\s\do10(i(а_ij a_i) x_j = 0 ; уравнение p(B): ;\s\do10(i(а_ij b_i) x_j = 0 ; B p(A)  ;\s\do10(iа_ij a_ib_j = 0  ;\s\do10(iа_ij b_ia_j = 0  A p(B) .Чтд.