23 Изображения плоских фигур в параллельной проекции.

1. любые два треугольника аффинно-эквивалентны и поэтому могут служить изображением друг друга.

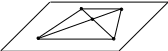2. не любой четырёхугольник может служить изображением данного четырёхугольника, а только тот,. у которого соответствующие диагонали делятся точкой пересечения в одинаковом отношении. Для построения изображения ABCD данного четырёхугольника A; ¯B; ¯C; ¯D; ¯ мы можем в качестве точек A, B, D выбрать произвольные три точки на плоскости изображений , не лежащие на одной прямой. Тогда вершина C определится однозначно.

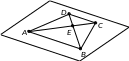
3. Аффинное отображение сохраняет параллельность прямых и отношение отрезков, лежащих на них. Поэтому изображением данной трапеции может служить только трапеция, у которой такое же отношение оснований. У этих трапеций одинаковое отношение оснований.

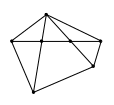4. Аффинное отображение сохраняет параллельность прямых. Поэтому изображением параллелограмма является параллелограмм. В качестве изображений трёх вершин параллелограмма можно выбрать любые три точки на плоскости изображений. Поэтому изображением данного параллелограмма может служить любой параллелограмм. Даже если A; ¯B; ¯C; ¯D; ¯ – ромб, прямоугольник или квадрат, всё равно его изображением может быть любой параллелограмм.

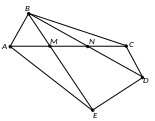
5. n-угольник при n5. Для построения его изображения 3 точки, изображающие 3 его вершины можно выбрать произвольно, а изображения остальных вершин можно найти, используя тот факт, что точки пересечения диагоналей оригинала и изображения делят соответствующие диагонали в одинаковом отношении.

Пусть, например, дан пятиугольник A; ¯B; ¯C; ¯D; ¯E; ¯. Пусть M; ¯ = A; ¯C; ¯  B; ¯E; ¯, N; ¯ = A; ¯C; ¯  B; ¯D; ¯. Выберем произвольные точки A, B, C. На отрезке AC находим точки M, N, такие что

(AC, M)= (A; ¯C; ¯, M; ¯), (AC, N)= (A; ¯C; ¯, N; ¯).

Затем на прямых BM и BN выбираем точки E и D так, чтобы

(BE, M)=(B; ¯E; ¯, M; ¯), (BD, N)=(B; ¯D; ¯, N; ¯).

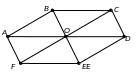
6. В правильном шестиугольнике A; ¯B; ¯C; ¯D; ¯E; ¯F; ¯ диагонали A; ¯D; ¯, B; ¯E; ¯, C; ¯F; ¯ делятся точкой пересечения O; ¯ пополам. В данном случае, в качестве произвольных удобнее выбрать точки A, B и O. Затем мы находим другие вершины, используя тот факт, что отрезки BC, OD и AO параллельны и равны; и также отрезки OE, AF и BO параллельны и равны.

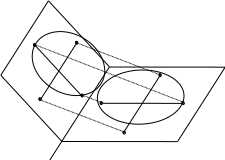
7. Изображение окружности и эллипса. Изображением окружности является эллипс, при этом перпендикулярные диаметры окружности изображаются сопряжёнными диаметрами эллипса.

Пусть  – произвольный эллипс, O – его центр, AB и CD – сопряжённые диаметры. Выберем репер R = {O, A, C}. Он определяет аффинную систему координат. Примем без доказательства, что относительно этой СК эллипс задаётся уравнением

x₁²+x₂²=1. (1)

Пусть ;¯ – ещё один эллипс, O; ¯ – его центр, A; ¯B; ¯ и C; ¯D; ¯ – сопряжённые диаметры. Выберем репер R ; ¯ = {O; ¯, A; ¯, C; ¯}. Рассмотрим аффинное отображение, которое переводит репер R ; ¯ в репер R . Поскольку оба эллипса имеют относительно соответствующего репера одно и то же уравнение (1), то при этом отображении ;¯ будет переходить в . Любые два эллипса аффинно-эквивалентны и поэтому могут служить изображением друг друга. В частности, изображением данной окружности может служить любой эллипс или окружность.