17. Абсолютная и относительная погрешности вычитания.

Погрешность разности: предельная абсолютная погрешность разности (u = x1 - x2) равна сумме предельных абсолютных погрешностей уменьшаемого и вычитаемого: Du = Dx1 + Dx2

Отсюда предельная относительная погрешность разности

где А - точное значение абсолютной величины разности чисел х1 и х2 .

Если приближенные числа х1 и х2 достаточно близки друг к другу и имеют малые абсолютные погрешности, то число А - мало. В этом случае из этой же формулы следует, что предельная относительная погрешность может быть весьма большой, т.е. происходит потеря точности.

Пример. Найти разность двух чисел х1 = 47.132 и х2 = 47.111 .

Решение. Разность u = 47.132 - 47.111 = 0.021 . Предельная абсолютная погрешность разности равна Du = 0.0005+0.0005=0.001 .

Предельные абсолютные погрешности вычитаемого, уменьшаемого и разности равны:

dx1 = 0.0005/47.132 = 0.00001

dx2 = 0.0005/47.111 = 0.00001

du = 0.001/0.021 = 0.05

Поэтому при приближенных вычислениях полезно преобразовывать выражения, вычисления числовых значений которых приводит к вычитанию близких чисел.

18. Метод сплайнов интерполяции данных: тип метода, количество и степень сплайн-полиномов, условие интерполяции и условия сопряженности сплайнов, эффективность метода.

В переводе с английского «spline» означает линейка. Если на плоскости отобразить некоторую функцию y = f(x) точками с коорди-натами (x_i, y_i), i = 0, 1, …, n, затем в этих точках зафиксировать стержни перпендикулярно плоскости, как это показано на рис. 2.1, и вставить между ними гибкую и упругую (стальную) линейку, то она примет форму, при которой запасëнная в ней упругая энергия будет минимальна.

Из теории изгиба бруса известно, что при малых деформациях геометрическая форма линейки (сплайна) будет представлять кривую, описываемую на каждом отрезке между точками (x_i, y_i), сопряжëн-ными кубическими полиномами.

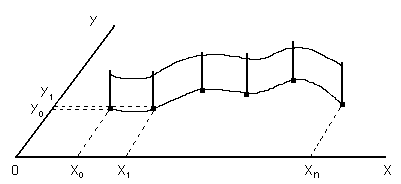
Рис. 2.1

На основе этого явления базируется метод представления дискретно (таблично) заданной функции y = f(x) непрерывной функ-цией – сплайном S(x), удовлетворяющим следующим условиям:

1) на каждом отрезке [x_i-1, x_i], i = 1, 2, …, n сплайн S(x), является полиномом третьей степени;

2) сплайн S(x), а также его первая и вторая производные непрерывны на интервале [x₀, x_n];

3) S(x_i) = y_i, i = 0, 1, …, n – равенство, называемое условием интерполирования.

На каждом из отрезков [x_i-1, x_i], i = 1, 2, …, n, строится полином третьей степени вида:

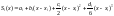, (2.13)

где x_i-1 ≤ x ≤ x_i,

a_i, b_i, c_i, d_i – коэффициенты, подлежащие определению.

Всего сплайн-полиномов n, значит, нужно определить 4n коэф-фициентов.

С одной стороны, при x = x_i имеем из выражения (2.13) a_i = S_i(x_i); с другой – из условия интерполирования имеем S(x_i) = y_i, Тогда можем записать:

a_i = y_i, i = 1, 2, …, n. (2.14)

Таким образом, коэффициенты a_i определены. Доопределим, кроме того, a₀ = y₀.

Теперь остается сформировать 3n уравнений для определения коэффициентов b_i, c_i, d_i. Для этого в распоряжении имеются условия непрерывности сплайнов, а также их первых и вторых производных (условия сопряжëнности):

S_i(x_i) = S_i+1(x_i), (2.15)

S'_i(x_i) = S'_i+1(x_i), (2.16)

S''_i(x_i) = S''_i+1(x_i), (2.17)

i = 1, 2, …, n – 1.

Воспользуемся условием (2.15). С учëтом выражения (2.13) для сплайна S_i(x) условие (2.15) при x = x_i примет вид:

.

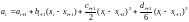Полученное уравнение справедливо при i = 0, 1, …, n – 1. Пере-пишем это уравнение при i = 1, 2, …, n:

.

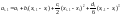Обозначим

h_i = x_i – x_i-1, (2.18)

тогда можем записать

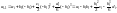
Из соотношения (2.14) имеем a_i = y_i, a_i-1 = y_i-1. С учëтом этого по-лучаем уравнения:

(2.19)

Таким образом, получили n уравнений. Ещë нужно 2n уравне-ний. Для их формирования воспользуемся условиями (2.16) и (2.17).

Сначала получим выражения для S'_i(x) и S''_i(x), продифферен-цировав выражение (2.13) для сплайна S_i(x):

, (2.20)

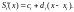(2.21)

Теперь запишем с учëтом выражений (2.20) и (2.21) условия (2.16) и (2.17). При x = x_i будем иметь

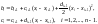
Перепишем эти уравнения, принимая i = 2, 3, …, n:

,

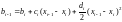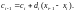
C учëтом обозначения (2.18) эти уравнения принимают вид:

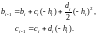
Окончательно получаем:

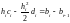, (2.22)

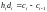, (2.23)

i = 2, 3, …, n.

Таким образом, имеем ещë 2(n – 1) уравнений. Объединяя урав-нения (2.19), (2.22), (2.23), получим систему из n + 2(n – 1) = 3n – 2 уравнений для определения 3n неизвестных коэффициентов b_i, c_i, d_i , i = 1, 2, …, n.

Недостающие два условия получим, предположив, что в край-них точках x₀ и x_n вторые производные от сплайн-полиномов равны нулю (это краевые условия):

S''₁(x₀) = 0,

S''_n(x_n) = 0.

Физическое обоснование такого предположения: начиная с крайних точек, единая материальная линейка, служащая физической моделью сплайн-интерполяции и отображаемая математически на каждом отрезке аппроксимации сопряжëнными сплайн-полиномами, имеет форму прямой линии, касательной к крайнему сплайну.

Первая производная от функции, отображающей такую пря-мую, проходящую под некоторым углом, является константой, а вто-рая, соответственно, равна нулю.

Раскроем краевые условия.

Из выражения (2.21) для первого сплайна при x = x₀ имеем

.

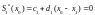С одной стороны, из обозначения (2.18) при i = 1 получаем x₀ – x₁ = – h₁. Тогда можем записать c₁ – h₁d₁ = 0 или h₁d₁ = c₁.

С другой – из (2.23) при i = 1 имеем h₁d₁ = c₁ – c₀, тогда c₁ = c₁ – c₀. Отсюда получаем дополнительное условие:

c₀ = 0. (2.24)

Из выражения (2.23) для последнего n-го сплайна при x = x_n имеем

,

отсюда получаем ещë одно дополнительное условие:

c_n = 0. (2.25)

В итоге для определения коэффициентов b_i, c_i, d_i (a_i заменены на y_i, i = 1, 2, …, n – табличные значения функции) имеем следую-щую систему уравнений:

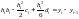, i = 1, 2, …, n, (2.19)

, i = 2, 3, …, n, (2.22)

, i = 2, 3, …, n , (2.23)

c₀ = 0, (2.24)

c_n = 0. (2.25)

Исключим из этой системы переменные b_i, d_i и получим систе-му уравнений, которая содержит только c_i. Для этого рассмотрим два соседние уравнения (2.19), чтобы получить разность b_i – b_i-1, стоящую в правой части уравнения (2.22):

,

,

отсюда

.

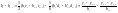После подстановки b_i – b_i-1 в (2.22) и приведения подобных чле-нов будем иметь:

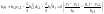. (2.22а)

Теперь исключим из (2.22а) коэффициенты d_i и d_i-1. Домножив (2.23) на h_i, запишем на основе этого уравнения два уравнения:

,

.

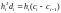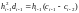После подстановки в (2.22а) приходим к уравнению:

, (2.22б)

i = 2, 3, …, n.

Эквивалентная запись уравнения (2.22б) при i = 1, 2, …, n – 1 (i на единицу меньше) будет

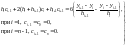(2.26)

Определив из (2.26) c_i, можем найти d_i и b_i:

– на основе (2.23) получаем

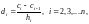(2.27)

при i = 1, ;

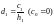– на основе (2.19) получаем

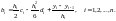(2.28)

Система (2.26) сразу не может быть решена, так как для опре-деления любого c_i надо иметь значения последующего c_i+1 и преды-дущего c_i-1. Если решать задачу с конечного i = n – 1, то для опреде-ления c_i известно только c_i+1 = c_(n-1)+1 = c_n = 0, а c_i-1 неизвестно.

Задача, казалось бы, неразрешимая. Однако имеется метод для решения таких задач – метод прогонки. Воспользуемся им.

Для сокращения записей перепишем систему (2.26) в следую-щем виде:

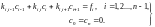(2.26а)

Здесь

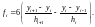
Будем искать решение систем (2.26а) в виде:

c_i = α_i+1 c_i+1 + β_i+1, i = 0, 1, 2, …, n – 1, (2.29)

где α_i+1, β_i+1 – неизвестные пока коэффициенты.

Выражение (2.29) можно переписать при i = 1, 2, …, n (i на еди-ницу больше) в виде

c_i-1 = α_ic_i + β_i.

Подставим сюда c_i из выражения (2.29):

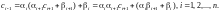
Итак, получили выражение для c_i и c_i-1 через c_i+1, т.е. можно исключить c_i и c_i-1 из (2.26а):

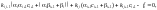
i = 1, 2, …, n – 1.

После приведения подобных членов получим окончательно:

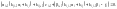
Это уравнение справедливо при выполнении условий:

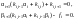
Из последних уравнений выражаем

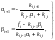(2.30)

i = 1, 2, …, n – 1.

Для начала расчëта α_i+1 и β_i+1 нужно знать значения α_i и β_i. Определим их.

Уравнение (2.29) при i = 0 можно записать в виде c₀= α₁c₁ + β₁. Ранее принято c₀ = 0, отсюда получаем α₁ = β₁ = 0.

Далее по формулам (2.30) находятся α₂ и β₂, …, α_n и β_n (это α_i+1 и β_i+1 при i = n – 1).

Имея значения всех прогоночных коэффициентов α и β можно вычислить по формуле (2.29) все значения коэффициентов c_i, начиная с конца (i = n, n – 1, …, 1):

• при i = n имеем c_n= 0;

• при i = n – 1 вычисляем c_i = α_i+1 c_i+1 + β_i+1, т. е. c_n-1 = α_nc_n + β_n,;

• в конце при i = 1 получаем c₁= α₂c₂ + β₂.

В заключение распишем более детально выражения (2.30):

из ранее принятого имеем:

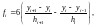
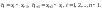
Интерполяция с помощью сплайнов позволяет представлять данные на каждом отрезке между заданными точками полиномами степени не выше третьей. Это в определëнной степени несущест-венный для инженерной практики недостаток метода сплайнов перед рассмотренными выше методами Лагранжа и Ньютона.

Однако сплайн-интерполяция имеет преимущество перед интерполяцией методами Лагранжа и Ньютона, состоящее в возмож-ности адекватного отображения реальных процессов, включая коле-бательные, представленные дискретно чередованием больших и ма-лых значений колеблющейся величины.

При использовании метода сплайнов вычисляемые по выраже-ниям сплайн-полиномов значения в промежуточных точках между узлами интерполяции не дают отклонений колеблющейся величины, превышающих реальные. Это объясняется тем, что физической моде-лью сплайн-интерполяции служит упругая линейка, принимающая форму, при которой запасенная в ней упругая (потенциальная) энер-гия будет минимальна (об этом было сказано в начале рассмотрения метода сплайнов).

Метод сплайн-интерполяции нашёл широкое применение в инженерной практике. Однако его не следует использовать для интер-поляции дискретно (по отдельным точкам) заданных кусочно-прямо-линейных зависимостей, отображаемых ломаными линиями. Это ограничение следует из свойства упругости линейки, лежащей в фи-зической основе метода. Упругая линейка не может принимать форму ломаной линии. Она всегда будет плавной кривой и только при доста-точно большом количестве заданных в узлах интерполяции точек приближается к отрезкам прямых.

Для интерполяции данных, представляемых кусочно-прямоли-нейными зависимостями, имеется метод линейной регрессии (част-ный случай аппроксимации данных рассматриваемым ниже методом наименьших квадратов).