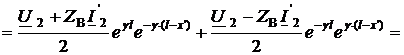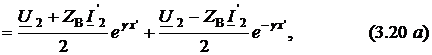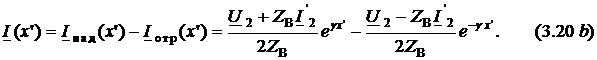- •7) Метод расчета нелинейных электрических цепей постоянного тока с использованием нагрузочной характеристики.
- •8) Метод расчета нелинейных электрических цепей постоянного тока с использованием результирующей вах.
- •26) Падающие и отраженные волны в длинных линиях
- •27) Волновые (вторичные) параметры длинной линии.
- •35) Особенности принципа действия варикапа
26) Падающие и отраженные волны в длинных линиях
Переходя от комплексных действующих значений напряжения и тока (3.3) к мгновенным, получаем
![]()
![]()
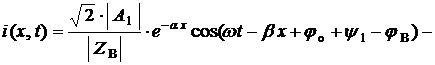
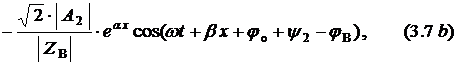
где ![]() –
начальная фаза,
–
начальная фаза, ![]() ,
, ![]() .
.
Первые
слагаемые в этих уравнениях описывают
падающие волны напряжения и тока
соответственно, т.е. волны, двигающиеся
от начала линии к её концу. Падающие
волны убывают с увеличением ![]() ,
что объясняется потерями при распространении
волны по линии. Вторые слагаемые описывают
обратные или отражённые волны напряжения
и тока, которые движутся от конца линии
к её началу и при этом убывают тоже из-за
потерь в линии (рис. 3.2).
,
что объясняется потерями при распространении
волны по линии. Вторые слагаемые описывают
обратные или отражённые волны напряжения
и тока, которые движутся от конца линии
к её началу и при этом убывают тоже из-за
потерь в линии (рис. 3.2).
Таким образом, мгновенное значение напряжения в любой точке линии определяется суммой падающей и отражённой волн напряжения, а мгновенное значение тока в любой точке линии определяется разностью падающей и отражённой волн тока.
Из
уравнений (3.7) следует, что напряжение
и ток в длинной линии зависят не только
от волновых параметров линии ![]() и
и ![]() в
явной форме, но и от внешних параметров
(сопротивления нагрузки или внутреннего
сопротивления источника эдс) через
коэффициенты
в
явной форме, но и от внешних параметров
(сопротивления нагрузки или внутреннего
сопротивления источника эдс) через
коэффициенты ![]() и
и ![]() в
неявной форме.
в
неявной форме.
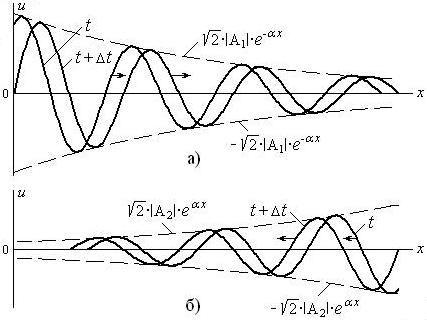
Рис. 3.2. Падающая (а) и отражённая (б) волны напряжения в длинной линии при гармоническом напряжении на входе
Величина ![]() характеризует
убывание амплитуды на единице длины
линии как падающей, так и отражённой
волн и поэтому носит название коэффициента
затухания. Коэффициент фазы
характеризует
убывание амплитуды на единице длины
линии как падающей, так и отражённой
волн и поэтому носит название коэффициента
затухания. Коэффициент фазы ![]() характеризует
изменение фазы, приходящееся на единицу
длины линии, и носит название коэффициента
фазы.
характеризует
изменение фазы, приходящееся на единицу
длины линии, и носит название коэффициента
фазы.
Длиной
волны ![]() называют
расстояние между двумя точками, фазы
которых отличаются на
называют
расстояние между двумя точками, фазы
которых отличаются на ![]() ,
то есть
,
то есть
![]()
Отсюда 
Скорость перемещения падающей волны называют фазовой и определяют как скорость перемещения точки, фаза колебаний в которой остаётся постоянной:
![]()
Отсюда  и
фазовая скорость получается равной
и
фазовая скорость получается равной

Следовательно, 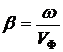 .
Подставляя эту зависимость в выражение
для
в
формуле (3.9), получаем известное уравнение
.
Подставляя эту зависимость в выражение
для
в
формуле (3.9), получаем известное уравнение
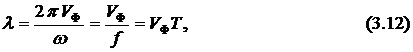
где  –
период гармонического колебания.
–
период гармонического колебания.
Запишем выражения (3.3) через падающие и отражённые волны:
![]()

Отсюда получаем соотношения
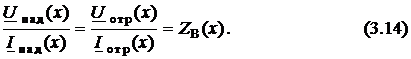
Для
однородной длинной линии выполняется
условие ![]() ,
и отношения (3.14) не зависят от координаты.
,
и отношения (3.14) не зависят от координаты.
Пусть
известны значения напряжения ![]() и
тока
и
тока ![]() в
начале длинной линии (точки 1 и
в
начале длинной линии (точки 1 и ![]() ),
то есть при
),
то есть при ![]() .
.
Уравнения (3.3) в этом случае преобразуются в
![]()

Решая совместно, получаем


Обычно
начало линии передачи бывает недоступно
для непосредственных измерений. Например,
у лабораторных генераторов оно находится
внутри корпуса прибора, у телевизионных
приёмников – в точке соединения
коаксиального кабеля с антенной, то
есть, как правило, на крыше здания. В то
же время конец линии практически всегда
доступен. Поэтому весьма часто расстояния
в линии отмеряют от конца, вводя
координату ![]() ,
где
,
где ![]() –
длина линии передачи (рис. 3.1).
–
длина линии передачи (рис. 3.1).
При ![]() или
или ![]() уравнения
(3.3) преобразуются в
уравнения
(3.3) преобразуются в
![]()
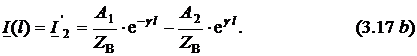
Преобразуя
уравнение (3.17 b)
относительно ![]() и
подставляя полученное выражение в
уравнение (3.17 a),
находим постоянные интегрирования
через параметры на конце длинной линии
и
подставляя полученное выражение в
уравнение (3.17 a),
находим постоянные интегрирования
через параметры на конце длинной линии
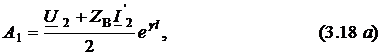
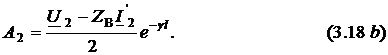
В
этих выражениях напряжение ![]() и
ток
и
ток ![]() можно
считать известными, так как они доступны
для измерений. Кроме того, они связаны
друг с другом по закону Ома:
можно
считать известными, так как они доступны
для измерений. Кроме того, они связаны
друг с другом по закону Ома:
![]()
Также
известно волновое сопротивление ![]() ,
а неизвестной является длина линии
.
,
а неизвестной является длина линии
.
Подставляя
коэффициенты ![]() и
и ![]() из
(3.18) в формулы (3.3) и переходя к координате
из
(3.18) в формулы (3.3) и переходя к координате ![]() ,
получаем запись уравнений через известные
величины:
,
получаем запись уравнений через известные
величины:
![]()