§29. Уравнения и передаточные функции многомерных объектов и систем управления в координатах вход - выход.

Р

ассмотрим многомерный объект управления (ОУ) или систему. Они имеют следующие входы и выходы :

- матрица - столбец(вектор) задающих (управляющих) воздействий размерностью (m x 1),

- вектор возмущающих воздействий,

- вектор управляемых величин,

где T - символ транспонирования.

Для этого объекта (системы) математическое описание в координатах вход – выход можно составить в двух формах:

- в виде системы дифференциальных уравнений;

- в виде одного векторно-матричного уравнения.

Систему дифференциальных уравнений целесообразно записать в операторной форме:

, i=1...m. (1)

Коэффициенты в (1) являются операторами, т.е. зависят от .

Соответствующее векторно-матричное уравнение:

, (2)

где матрица ,

Из (1) или (2) можно найти второй вид описания, а именно передаточные функции. По уравнению (1) п.ф находятся по методу суперпозиции, т.е. при нахождении п.ф. по одному входу все остальные полагают равными 0.

П.ф. по задающему воздействию , , .

П.ф. по возмущению , , .

Если воспользоваться уравнением (2) , то для нахождения п.ф. необходимо левую и правую часть уравнения умножить слева на обратную матрицу :

. (3)

Сопоставим (3) с уравнением, содержащим матрицы п.ф.:

Cравнение показывает, что

, ,

где обратная матрица ,

det A(p) – определитель матрицы A(p),

-алгебраическое дополнение к элементу матрицы А(р) находится известным образом, т.е. вычеркиванием из матрицы i строки и j столбца, вычислением получившегося определителя и умножением его на .

Матрица весовых функций получается применением обратного преобразования Лапласа к соответствующим матрицам п.ф., т.е.

; .

Матрицы ЧПФ получаются при подстановке в соответствующие матрицы п.ф.

§30. Математические модели одномерных и многомерных объектов и систем в пространстве состояний

Пространством состояний называется n-мерное (n- порядок уравнения ) пространство, по осям координат которого отложены переменные состояния .

Переменные состояния - это обобщенные координаты, которые позволяют в любой момент времени определить состояние объекта. Они образуют вектор состояния .

Применение переменных состояния является одной из основных тенденций расчета и проектирования. Переменные состояния обладают следующими особенностями:

1. это линейно-независимые переменные;

2. выбор переменных состояния произволен и неоднозначен;

3. переменные состояния не всегда имеют физический смысл.

Относительно переменных состояния система (объект) описывается уравнениями в нормальной форме Коши . Как известно, это уравнения первого порядка, разрешенные относительно первых производных по времени:

,

где - вещественные коэффициенты (постоянные, если система стационарна), g_j, v_j – задающие и возмущающие воздействия соответственно. Вместо этой системы из n уравнений можно использовать векторно-матричное уравнение состояний:

, (1)

где ,

Кроме этого уравнения для математического описания необходимо использовать уравнение выхода, связывающее вектор выходных величин с переменными состояния и входными воздействиями:

, (2)

где , , , .

Именно эта возможность выразить алгебраически выходные величины через переменные состояния и входные величины и означает, что переменные состояния в любой момент времени определяют состояние системы. Из уравнений (1) и (2) можно найти другие известные формы математического описания. Для нахождения матриц передаточных функций в уравнениях (1) и (2) при ННУ перейдем к изображениям по Лапласу и кроме того в уравнении (1) умножим левую часть на единичную матрицу I для возможности приведения подобных:

, (3)

где .

При вынесении за скобки справа в скобках остается характеристическая матрица sI-A .

Умножим левую и правую часть слева на матрицу, обратную характеристической матрице левой части:

. (4)

Подставив (4)в преобразованное по Лапласу (2)

, (5)

получим матрицы передаточных функций по задающему W^g(s) и возмущающему W^v(s) воздействям. Как известно, обратная матрица в знаменателе содержит определитель det характеристической матрицы, который является характеристическим полиномом системы и будучи приравнен к нулю дает характеристическое уравнение системы.

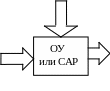
Пример 1

u

x₂

x₁=y

Запишем систему уравнений в нормальной форме Коши:

где ; ; ; ;

Характеристическое уравнение s²=0 имеет 2 нулевых корня.

В соответствии с (5) определим передаточную функцию

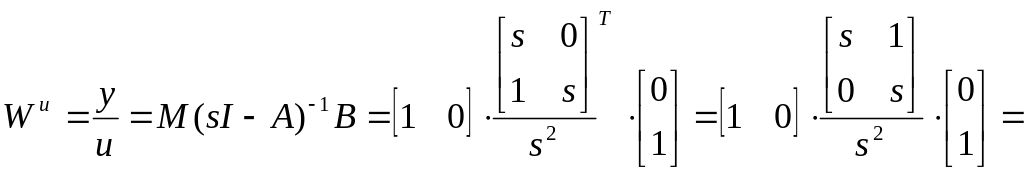
что очевидно для данного последовательного соединения .

Пример 2

Перейти от уравнения в координатах вход-выход

к

уравнениям в пространстве состояний.

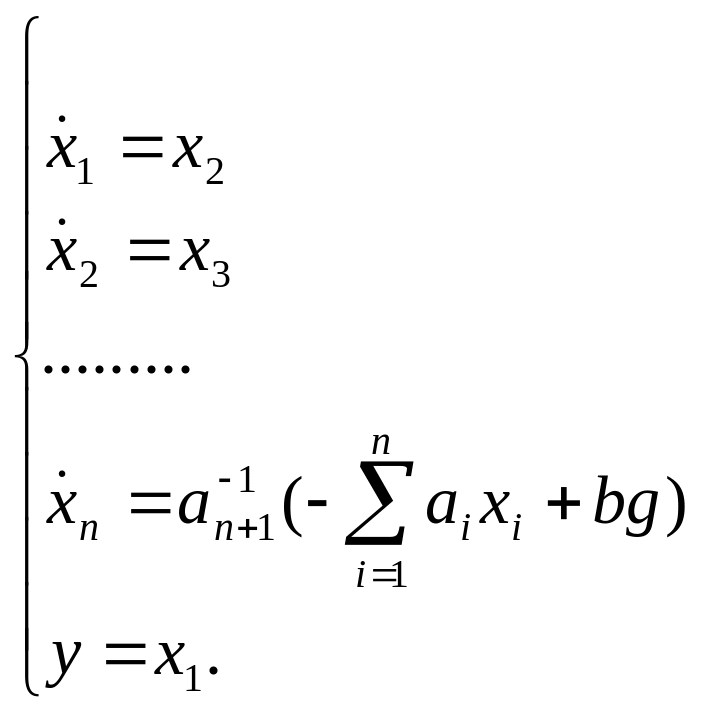
Принимаем в качестве переменных состояния выходную величину и ее производные по времени до (n-1) порядка включительно, что дает систему из n-1 уравнений состояний и уравнения выхода. Предпоследнее уравнение следует из заданного.

61