23. Математические операции над случайными величинами

Математические операции над случайными величинами

-Прерывные случайные величины X и Y называются независимыми, если не зависимы при любых i и j, события X=x_i и Y=y_j.

-Пусть случайная величина X принимает x₁, x₂, x₃, …, x_n с вероятностями p₁, p₂, p₃ ,…, p_n, соответственно, а Y-значения y₁, y₂, y₃, …, y_m, с вероятностями q₁, q₂, q₃, …, q_m.

а) Суммой случайных величин X и Y называется новая случайная величина Z=X+Y, которая принимает все значения вида z_ij=x_i+y_j(i=1,2,..n; j=1,2,...,m) с вероятностями p_ij, причем p_ij=P(X=x_i; Y=y_j)=P(X=x_i)*P_X=xi(Y=y_j).

-Если случайные величины X и Y независимые, то p_ij= p_i+ q_j.

Аналогично определяется разность и произведение случайных величин.

б) Разностью ( произведением) случайных величин X и Y называется новая случайная величина Z=X-Y (Z=XY), которая принимает все значения вида z_ij=x_i-y_j (z_ij=x_iy_j) с такими же вероятностями, с какими случайная величина Z=X+Y принимает соответствующие значения, т.е. p_ij= p_i+ q_j.

в) Произведением kX случайной величины Х на постоянную величину k называется новая случайная величина Z=kX, которая с теми же вероятностями, что и Х, принимает значения, равные произведениям значений случайной величины Х на k, т.е. =x_i².

г) Квадратом случайной величины Х, т.е. Х², называется новая случайная величина Z=X², которая с теми же вероятностями, что и Х, принимает значения, равные квадратам значений случайной величины Х, т.е. z_i=x_i².

 

24. Числовые характеристики дискретных случайных величин:

а) математическое ожидание и свойства

Свойства математического ожидания

1) Математическое ожидание постоянной величины равно самой постоянной.

2) Постоянный множитель можно выносить за знак математического ожидания.

3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.

Это свойство справедливо для произвольного числа случайных величин.

4) Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемы

Это свойство также справедливо для произвольного числа случайных величин.

Пусть производится п независимых испытаний, вероятность появления события А в которых равна р.

Теорема. Математическое ожидание М(Х) числа появления события А в п независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании.

Однако, математическое ожидание не может полностью характеризовать случайный процесс. Кроме математического ожидания надо ввести величину, которая характеризует отклонение значений случайной величины от математического ожидания.

Это отклонение равно разности между случайной величиной и ее математическим ожиданием. При этом математическое ожидание отклонения равно нулю. Это объясняется тем, что одни возможные отклонения положительны, другие отрицательны, и в результате их взаимного погашения получается ноль.

б) дисперсия дискретной случайной величины и ее свойства

Дисперсия случайной величины есть математическое ожидание квадрата соответствующей центрированной случайной величины.

Она характеризует степень разброса значений случайной величины относительно ее математического ожидания, т.е. ширину диапазона значений.

Расчетные формулы:

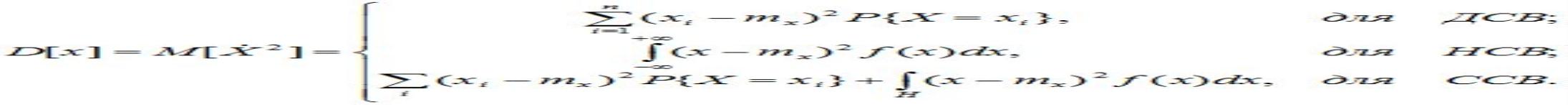
Дисперсия может быть вычислена через второй начальный момент:

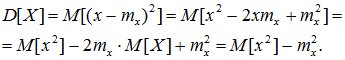
Дисперсия случайной величины характеризует степень рассеивания (разброса) значений случайной величины относительно ее математического ожидания. Дисперсия СВ (как дискретной, так и непрерывной) есть неслучайная (постоянная) величина.

Дисперсия СВ имеет размерность квадрата случайной величины. Для наглядности характеристики рассеивания пользуются величиной, размерность которой совпадает с размерностью СВ.

Средним квадратическим отклонением (СКО) СВ X называется характеристика

.

СКО измеряется в тех же физических единицах, что и СВ, и характеризует ширину диапазона значений СВ.

Свойства дисперсии

Дисперсия постоянной величины с равна нулю.

Доказательство: по определению дисперсии

При прибавлении к случайной величине Х неслучайной величины с ее дисперсия не меняется.

D[X+c] = D[X].

Доказательство: по определению дисперсии

3. При умножении случайной величины Х на неслучайную величину с ее дисперсия умножается на с².

Доказательство: по определению дисперсии

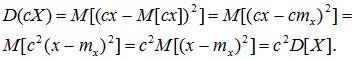
Для среднего квадратичного отклонения это свойство имеет вид:

Действительно, при ½С½>1 величина сХ имеет возможные значения (по абсолютной величине), большие, чем величина Х. Следовательно, эти значения рассеяны вокруг математического ожидания М[сХ] больше, чем возможные значения Х вокруг М[X], т.е. . Если 0<½с½<1, то .

Правило 3s. Для большинства значений случайной величины абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, или, другими словами, практически все значения СВ находятся в интервале: [ m - 3s; m + 3s; ].

в) среднее квадратическое отклонение, мода

Наиболее совершенной характеристикой вариации является среднее квадратическое откложение, которое называют стандартом (или стандартным отклонение). Среднее квадратическое отклонение ( ) равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической:

Среднее квадратическое отклонение простое:

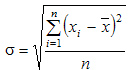
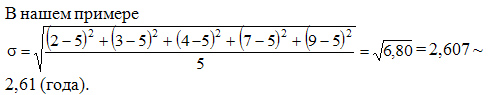
Среднее квадратическое отклонение взвешенное применяется для сгруппированных данных:

Между средним квадратическим и средним линейным отклонениями в условиях нормального распределения имеет место следующее соотношение: ~ 1,25.

Среднее квадратическое отклонение, являясь основной абсолютной мерой вариации, используется при определении значений ординат кривой нормального распределения, в расчетах, связанных с организацией выборочного наблюдения и установлением точности выборочных характеристик, а также при оценке границ вариации признака в однородной совокупности.