Лекция №04. Задача динамического программирования.

4.1. Задача об оптимальной последовательности операций

Пример 1. Овощная база должна разгрузить автомобилей и погрузить n₀ автомобилей. Необходимо спланировать последовательность операций обоих видов таким образом, чтобы суммарное время по приему и отправке всех машин было бы минимальным. Продолжительность операций в зависимости от текущего состояния указана в таблицах.

Пусть m₀ = 4, n₀ =3

Таблица 1. Разгрузка Таблица 2. Погрузка

m n	0	1	2	3		m n	0	1	2	3	4
0	7	10	11	15		0	9	10	13	16	20
1	9	9	10	12		1	11	12	14	13	16
2	10	12	11	15		2	12	10	11	14	17
3	11	14	12	16

Опишем состояние системы набором чисел (m, n), где m – число разгруженных автомобилей, n - число погруженных автомобилей. Из условия следует, что состояние системы характеризуется двумя параметрами: количеством машин, принятых для разгрузки товара и количеством машин, отправленных с товаром в магазины. Если по оси Х отложить число разгруженных машин (n), а по оси У – число загруженных товаром машин (m), то можно построить на плоскости граф состояний процесса, в котором каждая вершина характеризует состояние операции приема и отгрузки товара на оптовой базе. Дуги этого графа означают выполнение работы по приему или отправке товара на очередной машине. Горизонтальная дуга, идущая слева направо, соответствует разгрузке автомобиля, а вертикальная дуга, идущая снизу вверх, соответствует погрузке автомобиля. Каждой дуге можно сопоставить время, затраченное на выполнение операции по разгрузке или загрузке машины. Эту величину далее будем называть длиной дуги. Начальное состояние определяет начало процесса, а состояние соответствует окончанию процесса. Оптимизацию процесса будем проводить с конечного состояния . В соответствии с принципом динамического программирования, решение задачи начинаем с конечного состояния и далее рассматриваем вершины по мере уменьшения их ранга. Ясно, что Весь процесс разобьем на шаги, их количество k=n+m=3+4=7. Каждый шаг представляет собой сечение графа состояний, проходящее через вершины (на рисунке мы будем их показывать косыми линиями).

1. Условная оптимизация

1-ый шаг: к=1. На первом шаге с задаваемым сечением из вершин и возможен только один вариант перехода в конечное состояние . Поэтому в вершинах и записываем соответственно издержки 16 и 17. Ребра и обозначаем стрелкой, направленной в вершину (см. рис.):

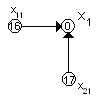
2-ой шаг: к=2. Второй шаг оптимизации задается сечением по вершинам , и . Из вершин и возможен единственный переход в вершины и соответственно, поэтому в вершинах и записываем суммарное время работы , необходимое для перехода в конечное состояние : 28 (12+16) и 33(16+17) соответственно. Из вершины возможны два варианта перехода: в вершину или в вершину . При переходе время работы составит 14+16=30, при переходе время составляет 15+17=32. Из двух вариантов выбираем наименьший и стрелкой обозначаем условно-оптимальный переход (см. рис.):

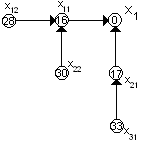
3-ий шаг: к=3. На третьем шаге сечение проходит через вершины , , и . Из вершин и возможен единственный переход в вершины и соответственно. Суммарное время работы для состояния равно 28+14=42, для состояния - 20+33=53. Из вершины возможны два варианта перехода: в вершину или в вершину .При переходе время работы составит 11+28=39, при переходе время работы будет 30+11=41. Из двух вариантов выбираем наименьший и стрелкой обозначаем условно оптимальный переход . Аналогично, из вершины также возможны два варианта перехода: в вершину или в вершину .При переходе время работы составит 13+30=43, при переходе время составляет 12+33=45. Из двух вариантов выбираем наименьший: . Получаем:

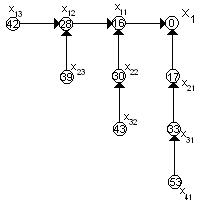
4-ий шаг: к=4. На четвертом шаге сечение проходит через вершины , , и . Из вершин возможен единственный переход в вершину . Суммарное время работы для состояния равно 11+42=53. Из вершины возможны два варианта перехода: в вершину или в вершину . При переходе время работы составит 10+42=52, при переходе суммарное время составляет 12+39=51. Из двух вариантов выбираем наименьший : .

Аналогично, из вершины также возможны два варианта перехода: в вершину или в вершину . При переходе время работы составит 14+39=53, при переходе время работы также составит 43+10=53. Поскольку времена одинаковы, подходят оба варианта. Наконец, из вершины возможны два варианта перехода: в вершину или в вершину . При переходе время составит 15+53=68, при переходе сумма составляет 16+43=59. Получаем:

5-ий шаг: к=5. На пятом шаге сечение проходит через вершины , и . Из вершины возможны два варианта перехода: в вершину или в вершину . При переходе время работы составит 12+53=65, при переходе время составляет 10+51=61. Из двух вариантов выбираем наименьший: .

Аналогично, из вершины возможны два варианта перехода: в вершину или в вершину . При переходе время работы составит 12+51=63, при переходе время составляет 9+53=62. Из двух вариантов выбираем наименьший: . Наконец, из вершины возможны два варианта перехода: в вершину или в вершину . При переходе время работы составит 13+53=66, при переходе сумма составляет 11+59=70. Из двух вариантов выбираем наименьший:. Получаем:

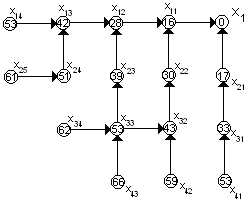
6-ий шаг: к=6. На шестом шаге сечение проходит через вершины и . Из вершины возможны два варианта перехода: в вершину или в вершину . При переходе время работы составит 11+61=72, при переходе время составляет 9+62=71. Из двух вариантов выбираем наименьший: .

Аналогично, из вершины снова возможны два варианта перехода: в вершину или в вершину . При переходе время работы составит 66+10=76, при переходе время составляет 62+10=72. Из двух вариантов выбираем наименьший: . Получаем:

7-ой шаг: к=7. На седьмом шаге сечение проходит через вершину из которой также возможны два варианта перехода: в вершину или в вершину . При переходе время работы составит 9+71=80, при переходе время составляет 7+72=79. Из двух вариантов выбираем наименьший . Имеем:

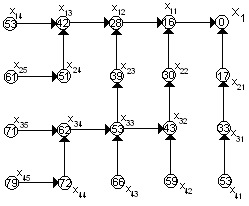
Итак, получен граф условно-оптимальных переходов. Минимально возможное время работы по обслуживанию всех семи машин на оптовой базе составляет 79 минут.

2. Безусловная оптимизация

Строим ориентированный граф перехода из состояния в состояние (см. рис).

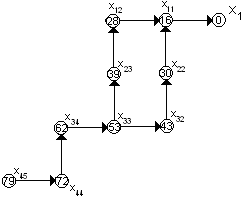
Минимальное время работы соответствуют следующим оптимальным путям на графе: и . Таким образом, в соответствии с решением, оптимальное управление процессом разгрузки и загрузки машин товаром состоит в следующем: на первом шаге следует разгрузить одну машину, на втором – загрузить одну. Далее возможны два варианта: 1) обслужить машину по разгрузке товара, две машины по загрузке и на последнем шаге разгрузить последнюю машину;2) обслужить две машины по загрузке товара, а затем две машины разгрузить.

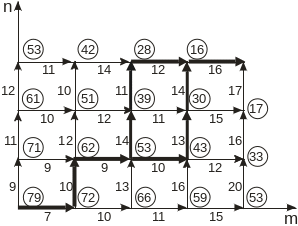
Заметим, что граф условно-оптимальных переходов можно строить и на рис.1 сразу. Тогда решение будет иметь вид:

4.2. Задача о кредитах (капитальных вложениях).