1. Непрерывность функции. Точки разрыва

1.Непрерывность функции в точке

Непрерывная функция — функция без «скачков», то есть такая, у которой сколь угодно малые изменения аргумента приводят к сколь угодно малым изменениям значения функции.

Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва.

 Определение. Функция f(x) называется непрерывной в точке х₀, если для любого положительного числа >0 существует такое число >0, что для любых х, удовлетворяющих условию

верно неравенство                                .

 

 Определение.  Функция f(x) называется непрерывной в точке х = х₀, если приращение функции в точке х₀ является бесконечно малой величиной.

 

f(x) = f(x₀) + (x)

где (х) – бесконечно малая при хх₀.

2 . Точка разрыва функции

1. Теорема о непрерывности функции в точке

3.Теорема о непрерывности обратной функции

Пусть y = f(x) - функция с областью определения X (D(f) = X) и областью значений Y (E(f) = Y). При этом разным значениям х отвечают разные значения y. Тогда для каждого значения y Î Y существует только одно x Î Х, такое , что f(x) = y. Если мы сопоставим каждому y Î Y именно такое x, то получим отображение множества Y в множество X. Это отображение называется обратным к данному отображению f и обозначается f -1 , т. е. обратная функция для y = f(x) есть x = f –1(y). Пусть y = f(x) (x Î D (f)) непрерывна и возрастает на отрезке [a; b], тогда обратная функция x = f—1(y) также непрерывна и возрастает на [f(a); f(b)]. (аналогично для непрерывной убывающей функции).

18. Односторонняя непрерывность. Точки разрыва, их 7классификация. Функция , определённая в некоторой окрестности точки х0, называется непрерывной в этой точке, если предел функции в точке х0 существует и равен значению в этой точке. Функция f(x), определённая на отрезке [a,b], называется непрерывной в точке а справа, если lim f(x)=f(a) (аналогично слева)

x®a+0

Функция y=f(x) непрерывна на Х, если эта функция непрерывна в каждой точке этого промежутка.

Если lim f(x) не равен lim f(x0)

X®Xo ,то х0 - точка разрыва непрерывности этой функции.

Классификация точек разрыва.

1. х0 – точка разрыва первого рода, если одосторонние пределы существуют, но они не равны между собой.

1.1 Точка устранимого разрыва, если односторонние пределы равны между собой, но их значение не совпадает со значением функции в этой точке.

Lim f(x)=lim f(x) не равен f(x0)

X®Xo-0 X®Xo+0

1.2 Точка разрыва с «конечным скачком». Правый и левый пределы не совпадают.

1.3 Точка разрыва с «бесконечным скачком». Хотя бы один односторонних

пределов бесконечен.

2. х0 - точка разрыва второго рода, если хотя бы один из

односторонних пределов не существует.

4 . Теорема о сохранении знака непрерывной функции

2)Производная функции. Правила вычисления производных. Таблицы производных.

1)Касательная к кривой

Уравнение касательной

Пусть функция задается уравнением y=f(x), нужно написать уравнение касательной в точке x0. Из определения производной: 

y/(x)=limΔx→0ΔyΔx

Δy=f(x+Δx)−f(x).

Уравнение касательной к графику функции: y=kx+b (k,b=const). Из геометрического смысла производной: f/(x0)=tgα=k Т.к. x0 и f(x0)∈ прямой, то уравнение касательной записывается в виде: y−f(x0)=f/(x0)(x−x0), или

y=f/(x0)·x+f(x0)−f/(x0)·x0.

2) Производная функция в точке Предел отношения приращения функции Δy к его приращению независимой переменной Δx, при стремлении Δx к нулю, то есть limΔx→0ΔxΔy=limΔx→0Δxf(x0+Δx)−f(x0), называется производной функции y=f(x) пo независимой переменной x, при данном ее значении (или в данной точке) x=x0.т получаем производну и в полученную функцию подставляем координаты х.

3)механический смысл производной. Производная пути по времени есть скорость. Производная скорости по времени или вторая производная пути по времени есть ускорение.

4) Геометрический смысл производной. производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.

5)Нормаль к кривой

Уравнение нормали

Нормаль -- это перпендикуляр к касательной (см. рисунок). Исходя из этого:

tgβ=tg(2π−α)=ctgα=1tgα=1f/(x0)

Т.к. угол наклона нормали -- это угол β1, то имеем:

tgβ1=tg(π−β)=−tgβ=−1f/(x).

Точка (x0,f(x0))∈ нормали, уравнение примет вид:

y−f(x0)=−1f/(x0)(x−x0).

6) Логарифмическая производная

Логарифмическая производная – производная от натурального логарифма модуля (абсолютной величины) – данной функции: 

Используя формулу производной сложной функции, найдем, что  (*)

Логарифмическую производную используют, например, при дифференцировании (нахождении производной или дифференциала) степенно-показательной функции.

ТЕОРЕМЫ МАТИХ ЕТИ!

1)Вывести уравнение касательной и нормали к кривой:  уравнение касательной можно привести к виду y=kx+b . Вспомним, что угловой коэффициент прямой k равен тангенсу угла наклона прямой к положительному направлению оси Ох или значению производной функции в точке проведения касательной , т.е. y=f `(х _о )· x+b.

Для вычисления воспользуемся тем, что касательная проходит через точку А(x _o ; f(x _o )), т.е. f(x _o )=f ´(x _o )·x +b, т.е. b = f(x _o ) – f ´(x _o )·x , т.е.

y=f `(х _о )· x+ f(x _o ) – f ´(x _o )·x , после преобразований имеем:

y = f(xo) + f ´(x _o ) · (x – x _o )

нормаль смотреть в определениях

2) Рассмотрим следующие вопросы, который касаются функций.

Если функция непрерывна, то она дифференцируема?

Если функция дифференцируема, то она непрерывна?

Ответ на первый вопрос: из непрерывности функции не следует ее дифференцируемость.

Ответ на второй вопрос: из дифференцируемости функции следует ее непрерывность.

Рассмотрим более конкретно каждый вопрос. Чтобы ответить на данные вопросы необходимо доказать озвученый факт или привести пример, который опровергает этот факт.

Найдем производную следующей функции   . Хорошо известно, данная функция является непрерывной и, что ее производная будет следующей:

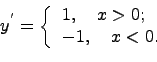
Покажем, что в точке нуль производная не существут. Для этого найдем производную в нуле по определению производной:

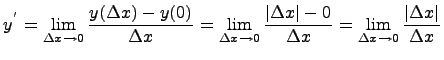
данный предел равен 1, если   и равен (-1), если   , получаем, что предел не существует, следовательно в нуле производной нет и функция в нуле не дифференцируема. 

 Если y = c, где c = const, то y' = 0.

Доказательство

Функция y = c принимает значение, равное c для любого аргумента x. Таким образом, Δy = 0при любом x. Следовательно,

Теорема доказана.

Теорема

3. Пусть функции u = u(x), v= v(x) дифференцируемы. Тогда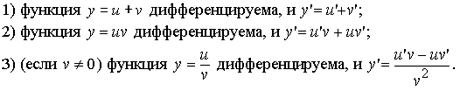 

Доказательство

Если аргумент x получит приращение Δx, то функции u, v получат приращения

Пусть y = u + v, тогда

Воспользовавшись свойством предела суммы функции, получаем

Утверждение 1) теоремы доказано.

Если y = u v, то   Прибавив и отняв в правой части этого равенства произведение  , после перегруппировки слагаемых получим  . Воспользовавшись свойствами предела функции, получаем

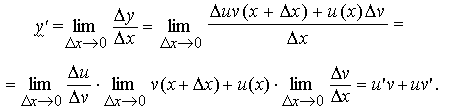
Утверждение 2) теоремы доказано.

Теперь, если 

Прибавив и отняв в правой части этого равенства частное  , после перегруппировки слагаемых получим

Далее аналогично доказываем утверждение 3). Теорема доказана.

Из теорем 2,3 следует, что постоянную можно выносить за знак производной, т.е. (cy)' = cy'

Если y(x)=f(u(x)) и существует f’(u) и u’(x), то существует y’(x)=f(u(x))u’(x).

Теорема о произв. обратной функции.

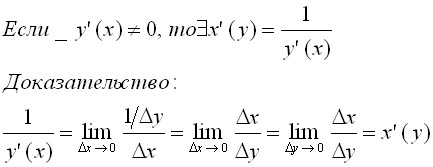
Производная обратной функции

Рассмотрим функцию y = f(x), для которой существует обратная функция x = g(y).

Теорема 5. Если обратная функция x = g(y) дифференцируема и g'(y) ≠ 0, то функцияy=f(x) дифференцируема, и 

Доказательство

Если аргумент x получит приращение Δx, то функция f получит приращение Δy = f(x + Δx) − f(x). С другой стороны, для обратной функции g приращения Δx, Δy связаны следующим образом:Δx=g(y + Δy) − g(y).

Тогда получаем

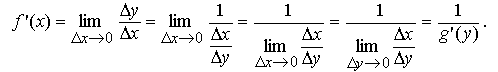
Теорема доказана.