4.4. Формула трапеций
Если подынтегральную функцию заменить полиномом первой степени на участке , то приближенное значение интеграла определится как площадь трапеции:
где
- значение второй производной
в точке
,
где она максимальна,
- шаг интегрирования,
- количество отрезков разбиения.
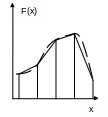
Рис. 2. Метод трапеций.
Метод трапеций, как и метод средних прямоугольников, имеет второй порядок.
Составная
квадратурная
формула трапеций для случая, когда точки
расположены
на равном расстоянии друг от друга, для
шага (длины элементарного отрезка)
при
на каждом отрезке
имеет вид:
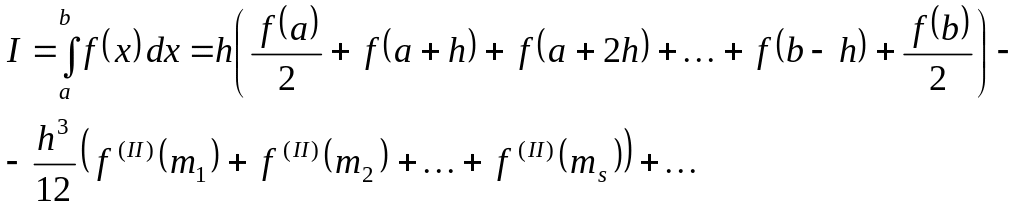
Или
,
где
.
На практике используют только
.
Если подынтегральная функция задана аналитически, то предпочтительнее из методов второго порядка применять метод средних прямоугольников вследствие его меньшей погрешности.
4.5. Метод Ньютона-Котесса
Метод основан на
интерполяции
в
пормежутках
полиномом Лагранжа. В общем случае
должна задаваться
ординатами. Формулы интегрирования
точны, если
- многочлен
-й
степени. При
получаем метод трапеций.
4.6. Формула Симпсона (метод парабол)
Этот метод является
частным случаем метода Ньютона-Котесса
при
.
Если подынтегральную функцию заменить полиномом второй степени на участке , то приближенное значение интеграла определится как площадь под параболой или формулой Симпсона:
где
.
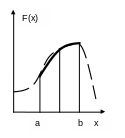
Рис. 3. Метод Симпсона (парабол).
Выражение для остаточного члена показывает, что формула Симпсона точна, даже если - многочлен третьей степени (погрешность трёхточечного правила Симпсона равна нулю, если -кубический полином). Эта частная особенность формулы Симпсона объясняет её преимущественное применение.
Формулой Симпсона называется интеграл от этого полинома на отрезке [a, b]:
Метод Симпсона имеет порядок погрешности 4 и алгебраический порядок точности 3.
Погрешность при интегрировании по отрезку [a,b] с шагом h определяется по формуле:
,
где
—
максимум четвёртой производной функции.
Так же, при невозможности оценить погрешность с помощью максимума четвертой производной (например, на заданном отрезке она не существует, либо стремится к бесконечности), можно использовать более грубую оценку:
,
где
—
максимум третьей производной функции.
Пример.
{$N+,E+,F+}
PROGRAM Integral;
{Вычисление определенного интеграла по формуле Симпсона}
Uses CRT;
{Глобальные переменные}
Type
RealType = Extended; {базовый вещественный тип}
FunType = Function(x : RealType) :RealType;
Var
A, B, Int : RealType;
N : Integer;
{$F+}
Function Fun(x : RealType) : RealType;
{Заданная подинтегральная функция}
Begin
Fun:= Cos(x*x);
End; {Fun}
{$F-}
Function Simpson(Fun : FunType;
A, B : RealType; N : Integer) : RealType;
{Вычисление определенного интеграла по формуле Симпсона}
{
ВОДНАЯ ИНФОРМАЦИЯ:
Fun - подынтегральная функция;
A, B - границы интервала интегрирования;
N - количество подынтервалов, на которые разбивается
интервал интегрирования.
ВЫХОДНАЯ ИНФОРМАЦИЯ:
Simpson - значения этой функции есть вычисленный по
формуле Симпсона определенный интеграл.
}
Var
h, I : RealType;
k : Integer;
Begin {Simpson}
h:= (B-A)/(N*2.0);
I:= Fun(A);
For k:= 1 to (2*N-1) do