Метод последовательных приближений

Рассмотрим задачу Коши для дифференциального уравнения первого порядка y^' = f(x,y) с начальным условием y(x₀) = y₀.

Метод последовательных приближений состоит в том, что решение y(x) получают как педел последовательности функций y_n(x) , которые находятся по рекуррентной формуле . Доказано, что если правая часть f(x,y) в некотором замкнутом прямоугольнике удовлетворяет условию Липшица по y: , то независимо от выбора начальной функции последовательные приближения y_n(x) сходятся на некотором отрезке [x₀,x₀ + h] к решению задачи. Если f(x,y) непрерывна в прямоугольнике R, то оценка погрешности приближенного решения y_n(x) на отрезке [x₀,x₀ + h] дается неравенством , где , а число h определяется из условия . В качестве начального приближения y₀(x) можно взять любую функцию, достаточно близкую к точному решению. Иногда , например, выгодно в качестве y₀(x) брать приближенное решение уравнения , полученное в виде частичной суммы степенного ряда.

Метод Эйлера

Метод Эйлера относится к численным методам ,дающим решение в виде таблицы приближенных значений искомой функции y(x). Рассмотрим дифференциальное уравнение y^' = f(x,y) с начальным условием y(x₀) = y₀. Выбрав достаточно малый шаг h, построим систему равноотстоящих точек x_i = x₀ + ih(i = 0,1,2,...). В методе Эйлера приближенные значения вычисляются последовательно по формулам y_{i + 1} = y_i + hf(x_i,y_i)(i = 0,1,2,...). При этом искомая интегральная кривая y=y(x) , проходящая через точку M₀(x₀,y₀), заменяется ломанной M₀M₁M₂... с вершинами  ; каждое звено M_iM_{i + 1} этой ломанной , называемой ломанной Эйлера, имеет направление, совпадающее с направлением той интегральной кривой уравнения , которая проходит через точку M_i.

Если правая часть уравения в некотором прямоугольнике удовлетворяет условиям , , то имеет место следующая оценка погрешности: , где y(x_n)-значение точного решения уравнения при x = x_n, , а y_n- приближенное значение, полученное на n-м шаге.

На практике иногда оказывается более удобным двойной просчет : расчет повторяют с шагом h/2 и погрешность более точного значения (при шаге h/2) оценивают приближенно так: .

Метод Эйлера легко распространяется на системы дифференциальных уравнений и на дифференциальные уравнения высших порядков. Последние должны быть предварительно приведены к системе дифференциальных уравнений первого порядка.

Рассмотрим систему двух уравнений первого порядка

с начальными условиями y(x₀) = y₀, z(x₀) = z₀.

Приближенными значения и вычисляются последовательно по формулам

Метод Рунге-Кутта

Рассмотрим задачу Коши для дифференциального уравнения y^' = f(x,y) с начальным условием y(x₀) = y₀.

Обозначим через y_i приближенное значение искомого решения в точке x_i. По методу Рунге-Кутта вычисление приближенного значения y_{i + 1} в следующей точке x_{i + 1} = x_i + h производятся по формулам

,

где

.

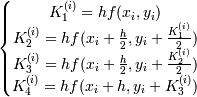Метод Милна

Пусть для уравнения y^' = f(x,y) кроме начального условия y(x₀) = y₀ известен "начальный отрезок", то есть значения искомой функции y(x_i) = y_i в точках x_i = x₀ + ih,(i = 1,2,3)- их можно найти одним из методов, изложенных выше. Последующие значения при i=4,5,... определяются следующим образом. Для предсказания используется первая формула Милна . Используя , находим и производим уточнение (коррекцию) по второй формуле Милна . Абсолютная погрешность ε_i более точного значения приближенно определяется по формуле . Эта формула позволяет на каждом шаге контролировать точность полученного результата. Если искомое решение требуется найти с точностью до ε и окажется, что ,то можем положить и перейти к вычислению y_{i + 1}.В противном случае следует уменьшить шаг h.

Метод Милна можно использовать для приближенного решения систем дифференциальных уравнений первого порядка,ма также уравнений высших порядков, которые предварительно следует преобразовать в такие системы.