Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Методичка по Тензорам3.DOC

Скачиваний:

Добавлен:

09.11.2019

Размер:

1.02 Mб

Скачать

☆

1 / 31 2 3 > Следующая >>>

3. Спектральные свойства тензоров второго ранга

3.1. Спектр тензора

1. Линейное пространство X называется алгеброй, если в нем введена алгебраическая операция умножения, удовлетворяющая аксиомам

а) ассоциативности ;

б) дистрибутивности

(x,y,z — произвольные элементы X, aÎR).

2. Если существует элемент e алгебры S такой, что для всех xÎS, то e называют единицей алгебры, а саму S — алгеброй с единицей.

Элемент x алгебры с единицей называют обратимым, если в алгебре найдется такой элемент x^-1, что

Любой элемент x алгебры с единицей имеет спектр — подмножество комплексных чисел lÎC, для которых элемент x - le необратим.

3. Простейшей алгеброй с единицей является множество комплексных чисел C. Единица здесь 1ÎR, операция умножения коммутативна. Кроме нуля любое комплексное число обратимо, поэтому его спектром оно само и является.

Менее тривиальный пример доставляют тензоры второго ранга из пространства . Умножение на этом множестве задает операция “×”, не являющаяся коммутативной. Единицей этой алгебры является тензор I. Среди тензоров есть как обратимые, так и необратимые элементы (называемые соответственно невырожденными и вырожденными тензорами). Спектральные свойства тензоров второго ранга будут изучаться в настоящей главе.

4. Тензор как линейный оператор ставит в соответствие трем произвольным некомпланарным векторам тройку векторов . С помощью этих векторов определим три скаляра

, (3.1.1)

, (3.1.2)

. (3.1.3)

Покажем, что скаляры не зависят от , а зависят только от . С использованием представления взаимного базиса (1.4.18) и трехчленного представления тензора (2.1.7)

получаем

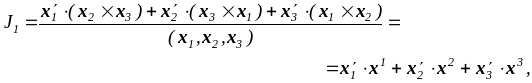
т.е.

(3.1.4)

Далее с использованием представления основного базиса (1.4.18) и формулы (1.4.16)

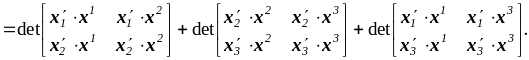
Попытаемся выразить результат через скалярные квадратичные по функции и . Используя трехчленное представление тензора,

Поскольку в нет квадратов, вычитаем из и получаем в точности . Поэтому

. (3.1.5)

Теперь с использованием (1.4.9) и (1.4.19)

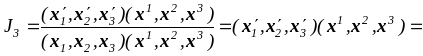
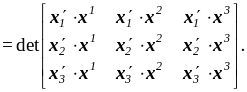
Попытаемся выразить результат через скалярные кубичные по функции , и . С использованием трехчленного представления тензора получаем выражения данных скаляров, из которых исключаем члены с кубами и квадратами скалярных произведений , которых нет в , в результате чего сразу получаем и в итоге

. (3.1.6)

Мы убедились, что скаляры действительно зависят только от самого тензора. Их называют инвариантами тензора. Попутно найдены выражения инвариантов тензора через следы первых трех его степеней.

5. Скаляр вводится как отношение объемов параллелепипедов, построенных на исходной некомпланарной и преобразованной тройках векторов. Компланарность , конечно, равносильна равенству . С другой стороны компланарность соответствует вырожденности тензора (п.2.1.7). Отсюда получаем удобный критерий: вырожденность тензора равносильна .

6. Докажем, что для любого тензора второго ранга справедливо тождество Гамильтона-Кэли:

. (3.1.7)

Для этого сначала приведем равенство (3.1.1) к виду

откуда ввиду произвольности следует

. (3.1.8)

Затем аналогичным образом исключим из равенства (3.1.2):

получая

. (3.1.9)

Подставим правую часть (3.1.8) в (3.1.9):

. (3.1.10)

Наконец, (3.1.3) представляется в виде

откуда

. (3.1.11)

Умножаем (3.1.10) справа на и подставляем в него правую часть (3.1.11):

и исключаем произвольный вектор , откуда и следует (3.1.7).

Тождество Гамильтона - Кэли означает линейную зависимость тензоров .

7. Поставим задачу отыскания спектра тензора T. На основании определения элемента спектра тензора и сказанного выше скаляр J₃, найденный для тензора T - lI по формуле (3.1.6), должен равняться нулю

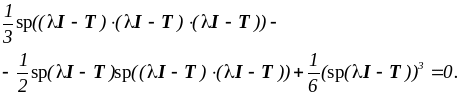(3.1.12)

Заметим, что

spI = 3, ,

, ,

и (3.1.12) принимает вид

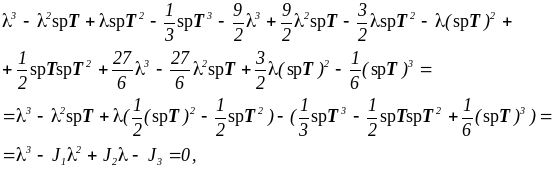
то есть

. (3.1.13)

Уравнение (3.1.13) называется характеристическим уравнением тензора . Корни характеристического уравнения тензора T — l₁, l₂, l₃ представляют собой спектр тензора и называются еще собственными значениями (собственными числами) тензора T.

Здесь читателю полезно самостоятельно вывести инварианты и характеристическое уравнение для тензора второго ранга над двумерным векторным пространством.

8. Если степени скаляра l в левой части (3.1.13) заменить соответствующими степенями тензора T, то получим тождество Гамильтона-Кэли. Соответствие указанных скалярного и тензорного уравнений обычно выражается утверждением, что тензор удовлетворяет своему характеристическому уравнению, и составляет суть теоремы Гамильтона-Кэли.

9. Обозначая за l₁, l₂, l₃ корни кубического уравнения (3.1.13), имеем по теореме Виета

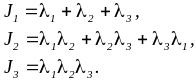(3.1.14)

В соответствии с (3.1.14)₃ для вырожденного тензора по крайней мере один из элементов его спектра равен нулю.

Числа l_i по определению могут быть комплексными, числа J_i— действительные, откуда и из (3.1.13) или (3.1.14) следует, что хотя бы один элемент спектра произвольного тензора есть действительное число, а два других — комплексно сопряженные.

10. Тензором с простым спектром назовем тензор с действительными попарно неравными собственными числами l₁¹ l₂¹ l₃¹ l₁. Кроме этого нас будут интересовать случаи тензоров с действительным кратным спектром, включающим два и только два совпадающих собственных числа l₁= l₂º l¹ l₃ либо три совпадающих собственных числа l₁= l₂= l₃º l.

Для тензора с двумя совпадающими собственными числами тождество Гамильтона - Кэли сводится к

(3.1.15)

где

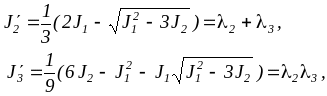
а для тензора с тремя совпадающими собственными числами — к

. (3.1.16)

11. Рассмотрим антисимметричные тензоры ( ). Для любого такого тензора

. (3.1.17) (5)

В самом деле, влечет , откуда . Но для любого тензора . С предыдущими эти равенства согласуются только при . Далее, , поскольку операция “°” задает скалярное произведение в пространстве тензоров второго ранга, откуда, используя условие , и получаем неравенство в (3.1.17).