76

4. Вопросы симметрии

4.1. Ортогональные преобразования

1. Рассмотрим сначала взаимно-однозначные линейные отображения на себя. Такие отображения осуществляются невырожденными тензорами, множество которых мы сейчас исследуем.

Множество замкнуто в отношении операции умножения, ибо из следует , и обратный тензор также является невырожденным, ибо . Поэтому согласно теореме о подгруппе множество есть группа, называемая полной линейной группой.

Для вектора линейное преобразование из осуществляется так:

, (4.1.1)

а для тензора, который можно воспринимать линейным оператором , из и следует закон

. (4.1.2)

В (4.1.1-2) подразумевались полярные объекты, вопроса линейных преобразований аксиальных объектов здесь мы касаться не будем.

Линейные преобразования из сохраняют спектр тензора, поскольку из и свойства детерминанта произведения тензоров следует

,

т.е. характеристические уравнения преобразованного и исходного тензоров совпадают. Следовательно, сохранятся и однозначно связанные со спектром тройки скаляров и (последнее можно проверить и непосредственно:

и т.д. Зависящие от полярного тензора T скаляры, не меняющие своего значения при линейных преобразованиях пространства , называются инвариантами тензора T относительно .

2. Рассмотрим теперь подмножество линейных преобразований из , сохраняющих скалярное произведение, т.е.

,

откуда

и, поскольку это выполняется для любых x и y,

, (4.1.3)

с другой стороны, так как  ,

.

Умножая (4.1.3) справа на и используя невырожденность , получаем

. (4.1.4)

Отсюда, в свою очередь,

. (4.1.5)

Такие преобразования называются ортогональными. Множество ортогональных преобразований замкнуто, поскольку из , и свойства следует . Кроме того, . По теореме о подгруппе множество является группой.

3. Ортогональное преобразование вектора и тензора запишется в форме (4.1.1-2) с учетом (4.1.4)

, , (4.1.6)

где  = 0 для полярных и  = 1 для аксиальных объектов. Эти законы происходят из природы объектов (чтобы убедиться в их справедливости, зеркально отразите аксиальный вектор, представляющий собой векторное произведение двух полярных векторов: получаемый результат будет направлен в противоположную сторону к интуитивно кажущемуся направлению). Закон преобразования полярного тензора в компонентах выглядит так

. (4.1.7)

По образцу (4.1.7) можно записать закон ортогонального преобразования тензора (здесь полярного) произвольного ранга:

. (1.4.8)

Из предыдущего раздела следует, что полярный тензор второго ранга может иметь до трех скаляров, инвариантных относительно преобразований из полной линейной группы. Поскольку при ортогональных преобразованиях евклидова пространства не изменяются углы между произвольными векторами, не изменятся и углы между парами главных направлений тензора при условии, что эти главные направления существуют. Например, тензор второго ранга, имеющий тройку попарно не ортогональных главных осей, после ортогонального преобразования пространства тензоров сохранит значения углов между этими главными осями. По этой причине любой тензор второго ранга может иметь до шести скалярных инвариантов относительно ортогональных преобразований пространства. Вектор не имеет инвариантов относительно линейных преобразований, но всегда имеет один инвариант относительно ортогональных — свою длину.

Вопрос об инвариантах аксиальных объектов оставляем для исследования читателю [Жилин П.А. Векторы и тензоры второго ранга в трехмерном пространстве. С.-Пб: Нестор, 2001. 275 с., Жилин П.А. Модифицированная теория симметрии тензоров и тензорных инвариантов // Изв. вузов. Сев.-Кавк. регион. Естеств. науки. 2003. Спецвыпуск. Нелинейные проблемы механики сплошных сред. С.176-195.].

4. Из (4.1.3) и свойств детерминанта , откуда . Ортогональные тензоры с детерминантом +1, называется собственно ортогональными, а с детерминантом -1 — несобственно ортогональными.

Собственные числа ортогонального тензора имеют единичный модуль, поскольку для каждого действительного из этих чисел существует собственный вектор , откуда , . Ранее было показано, что . Поскольку для любого тензора комплексных корней может быть только два (сопряженных), то для них (считая ) . В любом случае, все корни действительные или только один, с точностью до нумерации или - 1, а , где  — некоторое, зависящее только от O, вещественное число.

Пусть и . Тогда и имеет ; кроме того, , если , откуда множество собственно ортогональных тензоров наделено структурой группы, обозначенной далее .

5. Можно показать, что ортогональный тензор определяется тремя независимыми компонентами. Действительно, записывая условие (4.1.3) в ортобазисе, получим

.

Отсюда получаем шесть независимых связей на 9 чисел

откуда очевиден сделанный вывод.

Далее рассмотрим представления ортогонального тензора.

6. Диадное представление. Ортогональный тензор может быть представлен суммой трех диад ( — базис)

(4.1.9)

или

. (4.1.10)

7. Представление матрицей в ортобазисе. Используя формулу Гиббса, найдем компоненты O в ортобазисе

. (4.1.11)

Аналогично в ортобазисе

. (4.1.12)

Т.е. ортогональный тензор имеет в двух ортобазисах одинаковую матрицу компонент, и, кроме того, компоненты этого тензора в любом из этих базисов есть косинусы углов между соответствующими базисными векторами

. (4.1.13)

Отсюда следует

и

,

т.е. строчки (столбцы) компонент ортогонального тензора в ортобазисе попарно ортогональны, а сумма квадратов их элементов равна единице.

8. Инвариантное представление тензора. Из доказанного ранее ортогональный тензор всегда имеет собственное значение, равное 1 или -1. В первом случае тензор O преобразует соответствующий этому числу собственный вектор в себя, , а во втором — в противоположный вектор. Таким образом, для собственно ортогонального тензора векторы вдоль главного направления, соответствующего , не изменяются; для несобственно ортогонального тензора векторы вдоль главного направления, соответствующего , изменяются на противоположные.

Выберем первый элемент некоторого ортобазиса направленным вдоль такого главного направления. Из (4.1.11) . Отсюда следует, что образы базисных векторов , — векторы , — ортогональны первому главному направлению. Учитывая, что , изображаем конфигурацию этих векторов (рис. 4.1).

Рис. 4.1. Взаимное положение исходных и повернутых векторов ортобазиса.

Из рис. 4.1 и (4.1.11) можно записать более точное строение матрицы :

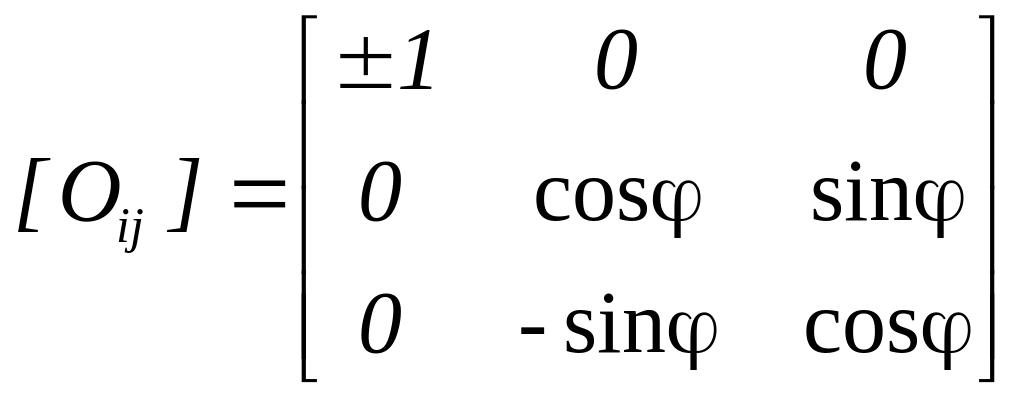. (4.1.14)

Итак, ортогональное преобразование, задаваемое собственно ортогональным тензором, представляет собой поворот относительно некоторой оси. Несобственно ортогональный тензор задает преобразование поворота относительно некоторой оси и отражение относительно центра. Последнее преобразование очевидно задается тензором -I, отсюда любой несобственно ортогональный тензор может быть представлен в виде , где — единственным образом определяемый собственно ортогональный тензор.

Воспользуемся представлением (4.1.9) в ортобазисе и (4.1.14)

или, поскольку ,

, (4.1.15)

где , знак “+” соответствует собственно ортогональному, а “–” —несобственно ортогональному тензорам. Инвариантное представление (4.1.15) ортогонального тензора записано с помощью вектора e (зависящего от O), относительно которого тензор O поворачивает пространство , и угла такого поворота . Ортогональный тензор с инвариантами e и  обозначается , где по прежнему “+” и “–” соответствуют собственно и несобственно ортогональным тензорам. Единичный вектор e задается двумя независимыми параметрами, например, сферическими координатами  и , а третий параметр есть . Это — хорошо известные углы Эйлера, задающие произвольный поворот абсолютно твердого тела в трехмерном евклидовом пространстве.

9. Кроме ортогональных тензоров для представления ортогональных преобразований с равным правом можно использовать кватернионы либо унитарные матрицы, где в качестве независимых параметров поворота применяются эйлеровы и кардановы углы, а также параметры Кэли - Клейна и Родрига - Гамильтона [Голубев Ю.Ф. Основы теоретической механики. М.: Изд. МГУ, 1992. 525 с.].

Известны также представления ортогональных тензоров множествами векторов и антисимметричных тензоров второго ранга с довольно сложно определяемой некоммутативной операцией сложения. Объекты, задающие ортогональные преобразования, вообще говоря, не могут образовывать линейные пространства, поскольку в последних операция сложения по определению коммутативна. Последовательно же осуществляемые конечные повороты в трехмерном пространстве коммутативностью не обладают, что легко проверить с помощью мысленного эксперимента (например, вращая прямоугольный параллелепипед на вокруг каких-либо двух из осей, направленных вдоль его ребер, с разной очередностью).

Связь антисимметричного и ортогонального тензоров получается при помощи представления экспоненты от антисимметричного тензора в виде степенного ряда:

Транспозиция этого выражения с помощью доказанных ранее правил приводится к виду

Перемножая эти ряды, получаем

,

т.е. в силу (4.1.3) тензор ортогональный

.

Из сказанного выше для и в общем случае имеем

.

10. Любой неособенный тензор единственным образом представляется произведением положительно определенного тензора на ортогональный или ортогонального на положительно определенный,

(4.1.16)

где , а L, R — положительно определены.

Доказательство полярного разложения (4.1.16) проведем конструктивно: построим для произвольного T компоненты разложения.

Из (4.1.16) имеем

(4.1.17)

причем положительно определен, поскольку таковым является : при .

Из (4.1.16) и (4.1.17) имеем

. (4.1.18)

Покажем его ортогональность

(использована симметричность , положительность ).

Аналогично строятся и .

Более точное строение компонент полярного разложения дает следующее утверждение.

Собственные значения тензоров L и R совпадают, а , где и — собственные векторы L и R соответственно.

Докажите его с помощью спектрального разложения тензоров L и R.

Таким образом, полярное разложение неособенного тензора записывается в виде

(4.1.19)

а

. (4.1.20)

Полярное разложение неособенного тензора T, задающего линейное преобразование пространства, разделяет его на последовательно выполняемые деформацию пространства, осуществляемую положительно определенным тензором, и ортогональное преобразование или наоборот (рис. 4.2).

Рис. 4.2. Геометрический смысл компонент полярного разложения.

Рекомендуется найти компоненты полярного разложения тензора простого сдвига в плоскости, заданного компонентами в ортобазисе

, .

Указание: используйте (4.1.17), равенство характеристических пространств тензоров и , формулы, дающие ориентацию первой главной оси симметричного тензора по отношению к первому вектору ортобазиса

,

и второе утверждение данного пункта.