3.3. Спектральное разложение

1. Предполагая, что существует тройка линейно-независимых собственных векторов в остальном произвольного тензора T — (и — сопряженных к ним), найдем компоненты разложения этого тензора в смешанном базисе, состоящем из левых и правых собственных векторов T. По формуле Гиббса и условию (3.2.18)

, (3.3.1)

то есть , , , а остальные . Диадное представление

(3.3.2)

называют спектральным разложением тензора.

2. Из (3.3.2) видно, что тензор T в базисе из диад, составленных из левых и правых собственных векторов этого тензора, имеет диагональную матрицу компонент. Верно и обратное: если тензор в некотором смешанном диадном базисе имеет диагональную матрицу компонент, то ненулевые диагональные компоненты являются собственными значениями тензора, а базисные векторы являются собственными векторами тензора. Докажем первое утверждение.

,

откуда , — собственные значения T.

Второе, проверим, что e_i, eⁱ являются собственными векторами тензора

, ,

то есть по определению e_i являются правыми собственными векторами тензора (eⁱ проверяются аналогично).

Определителем тензора назовем определитель матрицы смешанных компонент этого тензора. С учетом (3.3.2) получаем , но поскольку согласно () ,

. (3.3.3)

3. Для тензора с простым спектром спектральное разложение (3.3.2) неприводимо; в случае наличия двух и только двух кратных элементов спектра неприводимо следующее спектральное разложение:

,

а для спектра с тремя кратными элементами — следующее:

,

т.е. тензор оказывается шаровым.

4. Отметим, что если T — симметричный, а в остальном произвольный, то, согласно п.3.2.11, всегда существует базис , состоящий из взаимно ортогональных собственных векторов этого тензора, следовательно симметричный тензор всегда можно представить спектральным разложением

.

5. Если для тензора T существует спектральное разложение (3.3.2), то его непосредственным перемножением получаем

(3.3.4)

(n — натуральное), т.е. натуральные степени тензора разлагаются по одному и тому же спектральному базису.

Определители тензоров есть соответственно , то есть, как и для матриц, .

Для тензоров определены все операции, с помощью которых можно построить степенной ряд — сложение, умножение и умножение на число, — и тем самым определить аналитическую тензорную функцию f. В силу (3.3.4) получаем элементарный способ определения аналитической тензорной функции в спектральном базисе:

. (3.3.5)

6. Говорят, что два тензора с действительным спектром соосны, если их главные направления совпадают. Если спектр тензора простой, то существует единственная тройка главных направлений и, следовательно, существует спектральное разложение и справедливы представления (3.3.4). В этом случае можно видеть, что степени тензора соосны.

Если два тензора T и Q представляются спектральным разложением по одинаковому базису , , то операция их умножения коммутативна

T×Q = Q×T. (3.3.6)

Коммутируют, например, соосные тензоры, в том числе любые степени одного тензора. Если T — симметричный, а Q — ортогональный, то (3.3.6) выполняется тогда и только тогда, когда Q отображает каждое характеристическое пространство T само на себя. В том случае, если для пары тензоров условие (3.3.6) не выполняется, рассматривают коммутатор пары тензоров

T×Q - Q×T.

Покажите самостоятельно, что коммутируют два осесимметричных, но не соосных, тензора с характеристическими пространствами, схематически изображенными на рис. 3.3. Этот пример иллюстрирует, что для коммутируемости пары симметричных тензоров важны не типы их характеристических пространств (рис.3.2), а взаимное расположение последних. Изобразите все варианты характеристических пространств симметричных коммутирующих несоосных тензоров.

Рис. 3.3. Характеристические пространства некоторой пары коммутирующих тензоров.

7. Два тензора T и Q с действительным спектром называют пропорциональными, если совпадают их направления, т.е. T = cQ, cÎR . Пропорциональные тензоры соосны, но из соосности тензоров не следует их пропорциональность (рекомендуется показать). Пропорциональность двух соосных тензоров эквивалентна пропорциональности их соответствующих собственных чисел. Например, для и критерий запишется в виде

. (3.3.7)

Докажем в одну сторону: домножая T = cQ слева на правый собственный вектор t_i и справа на левый собственный вектор t ⁱ (i — любой), получим . В другую: из (3.3.7) и соосности T и Q имеем .

Для симметричного девиатора (для собственных чисел которого всегда справедливо равенство ) рассматривают функцию его собственных чисел (положим )

, (3.3.8)

называемую параметром Лоде. Изображая главные значения девиатора на действительной оси, легко увидеть (рис. 3.4), что параметр Лоде является характеристикой относительного положения на отрезке , и что . Можно доказать (сделать самостоятельно), что пропорциональность двух симметричных соосных девиаторов T и Q эквивалентна равенству их параметров Лоде

. (3.3.9)

Отсюда вытекает еще и такой критерий: два симметричных соосных девиатора пропорциональны тогда и только тогда, когда

(3.3.10)

для любой пары соответствующих собственных чисел.

Рис. 3.4. Смысл параметра Лоде

8. Рассмотрим трехмерное пространство (симметричных) тензоров, разложимых в виде (3.3.2) по тройке диад . Выберем такую нумерацию осей, чтобы для рассматриваемых тензоров было . В этом пространстве рассмотрим тригонометрический ортобазис

(3.3.11)

с первым элементом, равнонаклоненным к осям , а вторым и третьим — располагающимся в плоскости, равнонаклоненной к осям , так, как изображено на рис.3.5. Поскольку , а , т.е. , плоскость, натянутая на и , содержит только девиаторы и называется девиаторной плоскостью, а прямая, натянутая на , — только шаровые тензоры и называется шаровой осью. В девиаторной плоскости вводится полярная система координат с отсчитываемым от углом , называемым углом вида, и модулем .

Таким образом, кроме собственных значений , тензор из рассматриваемого пространства может быть охарактеризован тройкой чисел

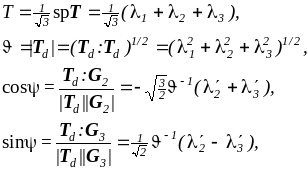(3.3.12)

где (иначе нарушается соглашение ). Два последних уравнения (3.3.12) с учетом равенства могут быть разрешены относительно :

(3.3.13)

Параметр Лоде тогда выразится в виде

, (3.3.14)

поэтому пропорциональность девиаторов (с одинаковой упорядоченностью собственных чисел) эквивалентна равенству их углов вида.

Рис.3.5. Базис в девиаторной плоскости.

Рассматриваемые тензоры в тригонометрическом ортобазисе представляются в виде

. (3.3.15)

Нетрудно получить таблицу умножения и ,

(3.3.16)

с помощью которой элементарно показывается, что девиатор произведения двух девиаторов и есть

(3.3.17)

и, в частности, что

(3.3.18)

— угол вида квадрата девиатора равен удвоенному углу вида этого девиатора, взятого с отрицательным знаком.

9. Положительно определенным называется симметричный тензор T, если (то есть для всех ненулевых аргументов значение построенной на этом тензоре квадратичной формы положительно). Эквивалентно, если существует положительный скаляр , что , то тензор T называется положительно определенным.

Докажем, что симметричный тензор T положительно определен тогда и только тогда, когда его собственные значения положительны.

Необходимость:

возьмем x = t _k, , тогда

.

Достаточность:

— любой, .

На практике удобно применять критерий Сильвестра: положительная определенность симметричного тензора означает положительность всех его главных миноров. По предыдущей теореме из следует . С другой стороны, если , то обязательно и .

10. Для положительно определенного тензора можно определить его корни:

, что , (3.3.19)

где n — натуральное число. С учетом (3.3.4)

,

а , откуда и для нечетных n и для четных. Таким образом, в спектральном виде корни находятся как

(3.3.20)

Ранее говорилось, что для любого тензора второго ранга определена натуральная степень, а для неособенных — целая степень. Для положительно определенных тензоров определена любая рациональная степень.

11. С помощью развитой в данной главе теории изучим алгебраические свойства полусимметричных тензоров четвертого ранга , обладающих симметрией

Умножение в данной алгебре задается операцией “:”.

Построим взаимно-однозначное отображение такой алгебры с алгеброй симметричных тензоров второго ранга над пространством , задаваемое соотношениями между элементами ортобазисов пространств и

(3.3.21)

с помощью которых можно получить связь компонент с компонентами — симметричного тензора второго ранга над пространством .

Нетрудно увидеть, что размерность пространства, над которым определены тензоры второго ранга, определяет число элементов спектра (среди которых возможны совпадающие). Поэтому, переформулировав результаты п.3.2.12, заключаем, что тензоры из всегда имеют действительный спектр, состоящий из шести элементов, и шесть ортонормированных собственных векторов. То же можно сказать и для полусимметричных тензоров с отличием лишь в том, что их собственные “векторы” на самом деле являются тензорами из . Эти собственные тензоры, как и спектр, можно отыскать сначала в пространстве , а затем с вернуться в исходное пространство. С использованием перехода в легко выполняется обращение тензора четвертого ранга, сводящееся к привычному обращению матрицы.

Отображая тензор с помощью (3.3.21), получите единичный элемент алгебры полусимметричных тензоров четвертого ранга. Рекомендуется также построить единичный элемент алгебры полусимметричных тензоров четвертого ранга над .