§ 1.5. Невироджені системи лінійних рівнянь. Матричний метод. Ф ормули Крамера.

Розглянемо систему n лінійних рівнянь із n невідомими :

Д ля системи (5.1) маємо

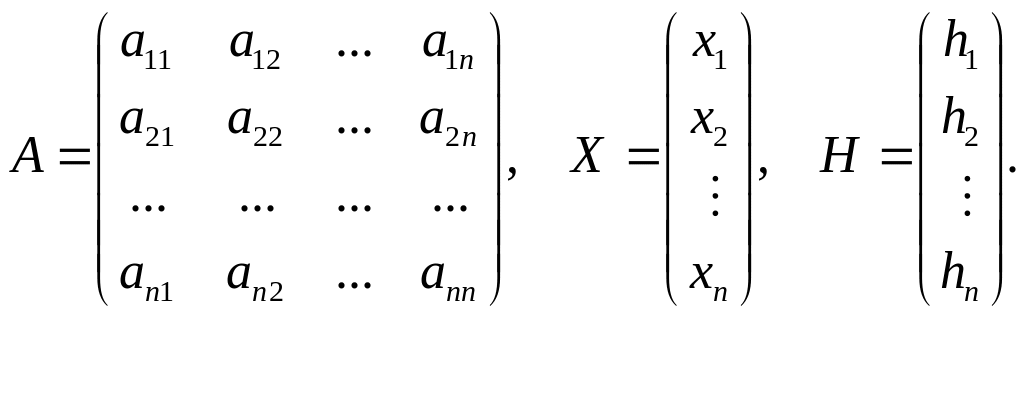Якщо визначник матриці А відмінний від нуля, то система (5.1) називається невиродженою. У випадку, коли detA = 0, кажуть, що система вироджена.

Нехай система (5.1) є невиродженою. Перепишемо її у матричній формі :

. (5.3)

Помноживши рівняння (5.3) на обернену матрицю А^-1 зліва, здобудемо :

Якщо невироджена система (5.1) розв’язується за допомогою формули (5.4), то кажуть, що вона розв’язана матричним методом. При застосуванні цього методу необхідно знаходити обернену матрицю А^-1 (так як detA 0, то обернена матриця обов’язково існує).

Невироджена система (5.1) може розв’язуватись також за формулами Крамера :

де  = detA – визначник матриці системи; ₁ – визначник, який здобудемо з визначника  за допомогою заміни першого стовпчика стовпчиком вільних членів; ₂ – визначник, який здобудемо з визначника  за допомогою заміни другого стовпчика стовпчиком вільних членів; і т.д.

Приклад 1. Розв’язати дану систему :

а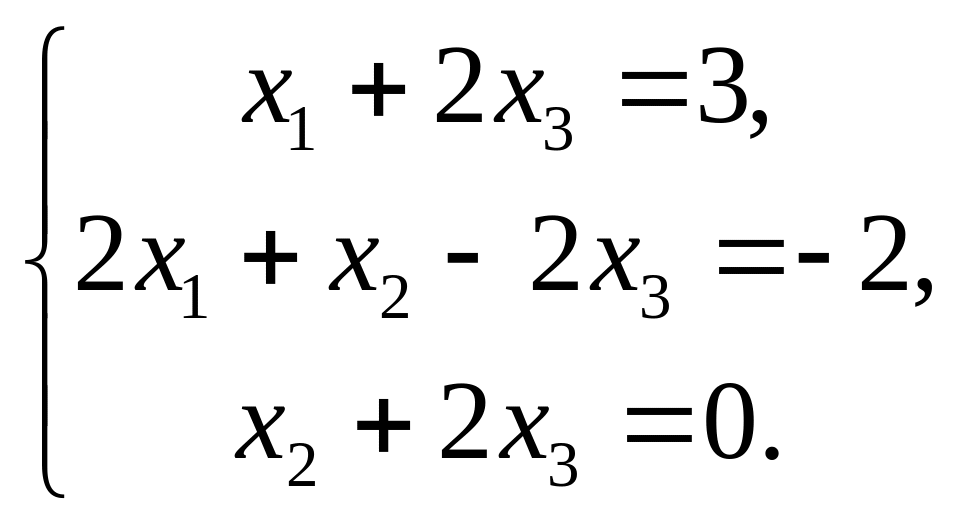 ) за формулами Крамера; б) матричним методом .

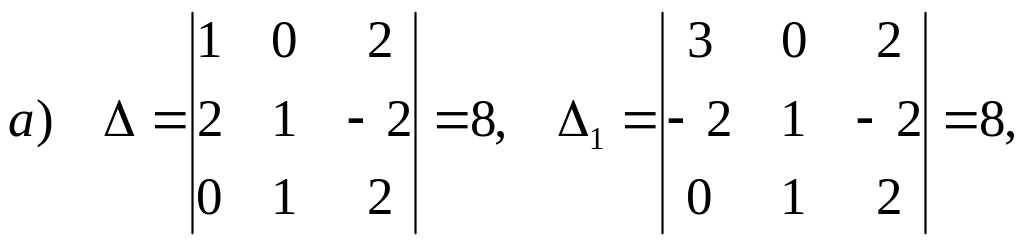Розв’язання.

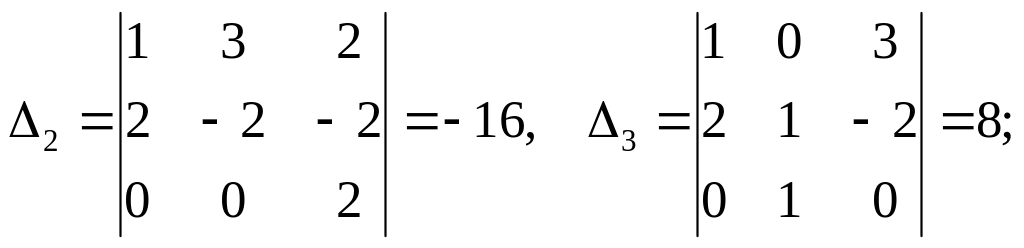
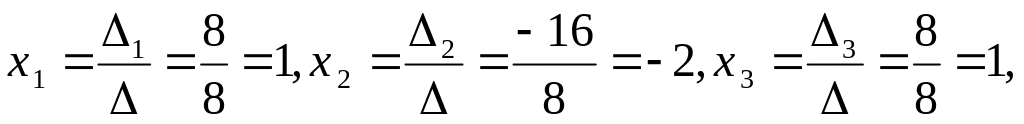
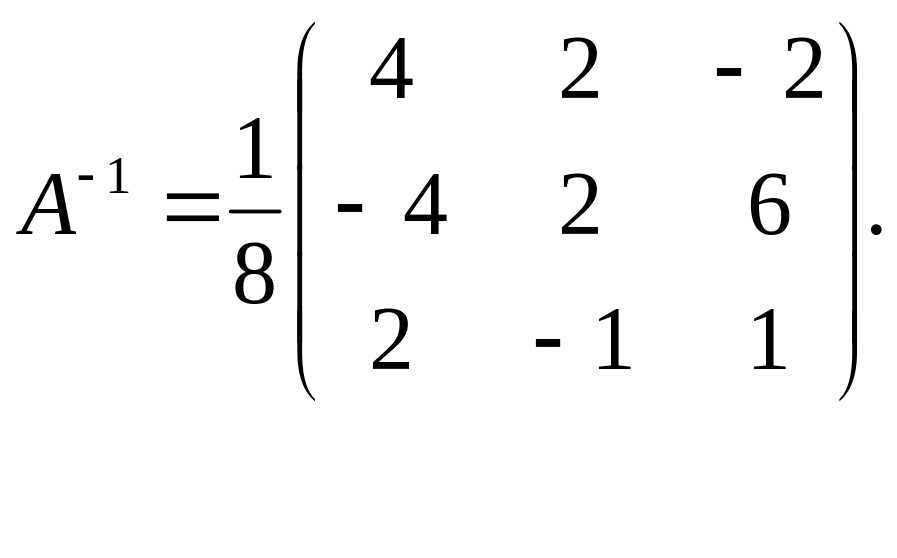б) Знаходимо спочатку обернену матрицю А^-1 (див § 1.3.):

З астосовуэмо формулу (5.4):

Таким чином

§ 1.6. Критерій сумісності та загальна схема дослідження і розв’язування системи лінійних рівнянь.

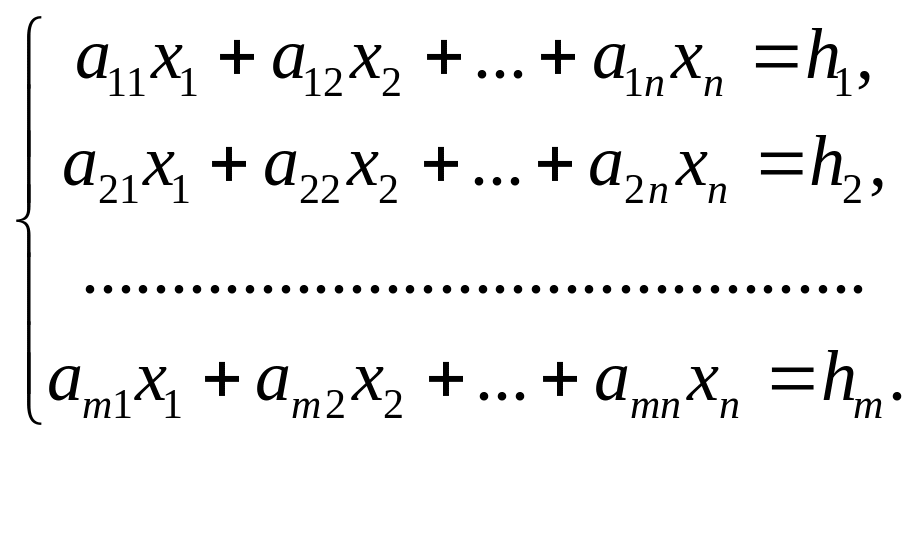Нехай задана система лінійних рівнянь.

Питання про існування розв’язків цієї системи розв’язується сформульованою нижче теоремою.

Теорема Кронеккера–Капеллі (критерій сумісності системи лінійних рівнянь): для сумісності системи (6.1) необхідно й достатньо, щоб ранг матриці системи дорівнював рангу її розширеної матриці.

Наведемо загальну схему дослідження й розв’язування системи лінійних рівнянь (6.1).

1) Визначаємо – ранг матриці і - ранг розширеної матриці системи. Якщо то система несумісна (на цьому дослідження закінчується). Якщо ж то переходимо до наступного кроку.

2) Виділяємо базисний мінор матриці А, тобто відмінний від нуля мінор, порядок якого дорівнює рангу матриці.

3) Виписуємо ті рівняння системи (6.1), числові коефіцієнти яких (частина або усі) утворюють базисний мінор. Складена таким чином система еквівалентна системі (6.1). Якщо ранг матриці r дорівнює числу невідомих n, то здобута система невироджена, має єдиний розв’язок і може бути розв’язана будь–яким методом. Якщо ж r < n, то переходимо до наступного кроку.

4) Виділяємо основні (базисні) і вільні невідомі. Невідомі, коефіцієнти при яких увійшли у базисний мінор, вважаємо основними. Решту n-r невідомих вважаємо вільними. Вільні невідомі позначаємо через с₁,с₂,…,с_n-r і переносимо у праві частини рівнянь. Розв’язуємо здобуту систему відносно основних невідомих будь–яким методом (система невироджена).

Приклад 1. Дослідити дану систему й у випадку сумісності розв’язати її.

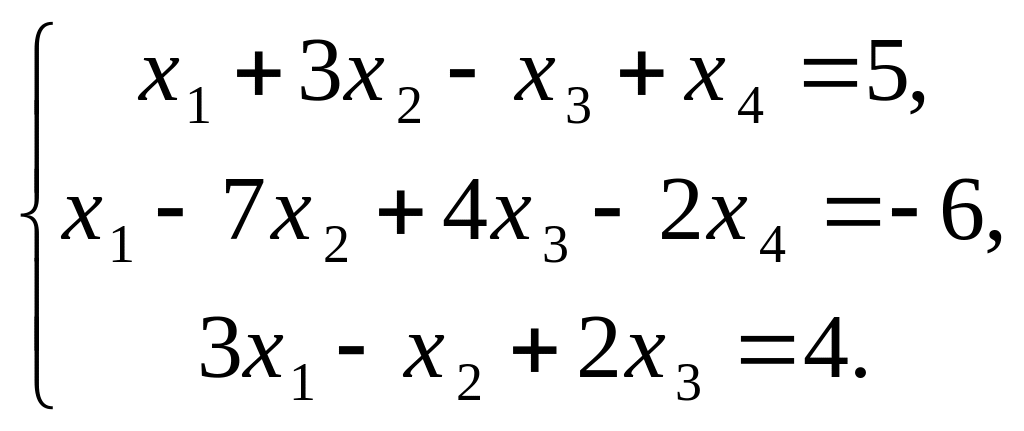
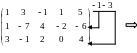Розв’язання. Знайдемо ранг розширеної матриці (див § 1.3). Елементарні перетворення застосовуємо тільки для рядків.

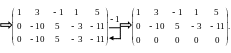Отже, (число ненульових рядків). Остання матриця визначає також і ранг матриці системи. Він дорівнює числу ненульових рядків указаної матриці без останнього стовпчика (без стовпчика вільних членів). У відповідності зі сказаним . Таким чином, Отже, система сумісна.

Виділяємо базисний мінор, тобто відмінний від нуля мінор другого порядку матриці А. Базисним може бути, наприклад, наступний мінор (два перших рядки і два перших стовпчики):

Т ак як базисний мінор утворений з коефіцієнтів при х₁ і х₂ перших двох рівнянь даної системи, то х₁ і х₂ - основні невідомі і далі розглядаємо таку систему :

В ільні невідомі х₃ та х₄ позначаємо через с₁ і с₂ відповідно. Перепишемо систему у вигляді :

Застосовуємо формули Крамера.

Таким чином, система має нескінченну множину розв’язків: х₁=(17-5с₁-с₂)10, х₂=(11+5с₁-3с₂)10, х₃=с₁, х₄=с_2, де с₁, с₂ – будь–які дійсні числа.