§ 2.6. Векторний добуток векторів.

Упорядкована трійка ненульових векторів називається правою, якщо після зведення її до спільного початку для спостерігача, що знаходиться на кінці вектора , поворот на найменший кут від вектора до вектора здійснюється проти руху годинникової стрілки (рис.8).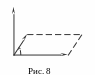

Векторним добутком двох неколінеарних векторів і називається вектор , який визначається наступними трьома правилами:

1. довжина вектора задається формулою

, (6.1)

де – кут між векторами і ;

2. вектор перпендикулярний до кожного з векторів і ;

3. вектори утворюють праву трійку векторів (рис.8).

Перше правило визначає довжину вектора , а два останні –його напрям. Легко бачити, що добуток правої частини формули (6.1) дорівнює площі паралелограма, побудованого на векторах і . Отже, довжина вектора дорівнює площі вказаного паралелограма.

Вважається, що векторний добуток двох колінеарних векторів дорівнює нульовому вектору.

Векторний добуток векторів і будемо позначати або .

Властивості векторного добутку:

1. ;

2. ;

3. ;

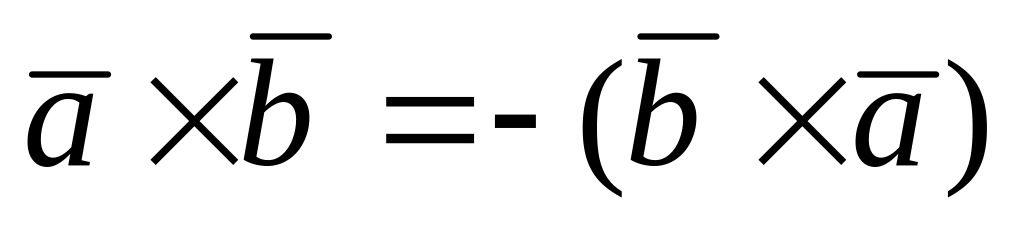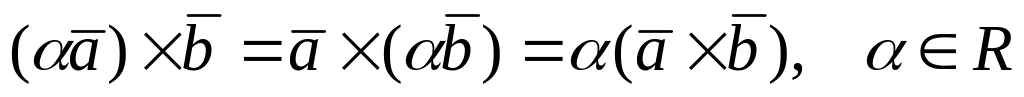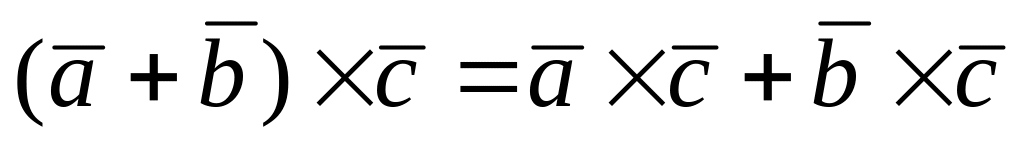4. якщо векторний добуток двох ненульових векторів і дорівнює нульовому вектору, то вектори і колінеарні.

Нехай вектори і задані своїми координатами:

Тоді:

, (6.2)

або

. (6.3)

Площа паралелограма й площа трикутника, побудованих на векторах і , обчислюються наступним чином:

, . (6.4)

Приклад 1. Задані два вектори і . Знайти: а) вектор, перпендикулярний до кожного з векторів і ; б) площу трикутника, побудованого на векторах і .

Розв’язання. а) Відмітимо, що задача не має єдиного розв’язку, тобто існує нескінченне число колінеарних векторів, які задовольняють умовам цієї задачі. Одним із таких векторів є векторний добуток (див. означення):

.

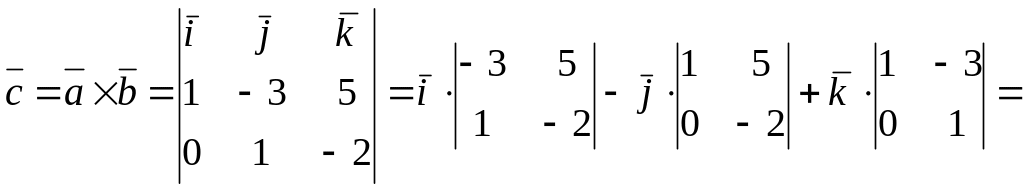
б) Використовуючи (6.4), здобудемо

(кв. од.).

§ 2.7. Мішаний добуток векторів.

Скалярний добуток векторів і називається мішаним добутком векторів і позначається або . Таким чином, у відповідності з означенням, можемо записати

. (7.1)

Властивості мішаного добутку:

1) мішаний добуток не змінюється, якщо в ньому поміняти місцями операції векторного й скалярного добутку:

2) мішаний добуток не змінюється при циклічній перестановці векторів:

3) при перестановці місцями будь–яких двох векторів мішаний добуток змінює знак на протилежний:

Якщо вектори і задані своїми координатами, то

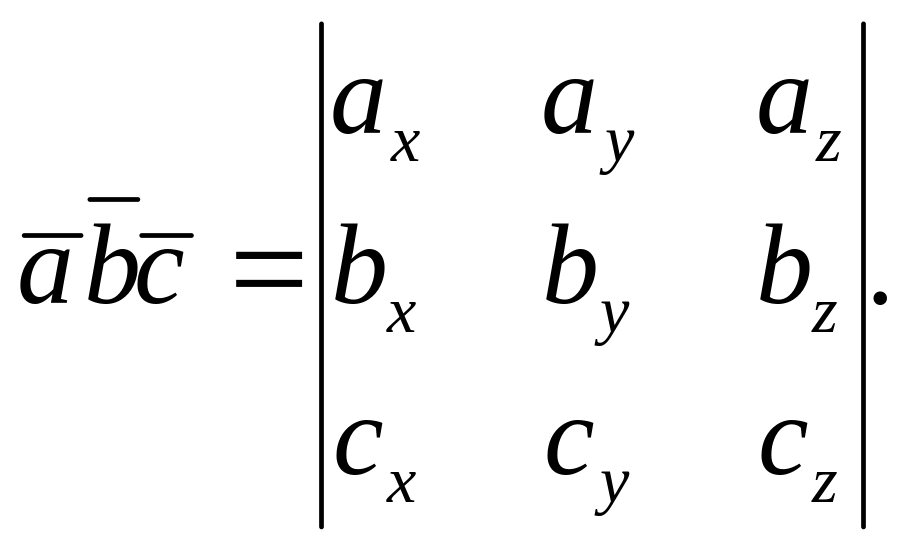(7.2)

Модуль мішаного добутку некомпланарних векторів дорівнює об’єму паралелепіпеда, побудованого на цех векторах. Отже об’єм паралелепіпеда й піраміди, побудованих на векторах можуть бути знайдені за формулами:

(7.3)

Приклад 1. Точки є вершинами чотирикутної піраміди. Знайти її об’єм.

Розв’язання.

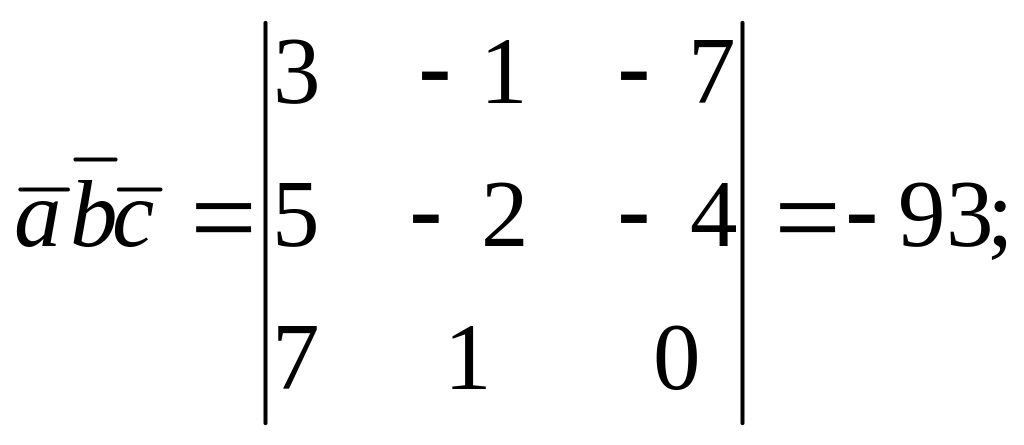
(куб. од).

Використовуючи поняття мішаного добутку, умову компланарності (лінійної залежності) трьох ненульових векторів можна представити у вигляді

(7.4).

Якщо мішаний добуток трьох ненульових векторів відмінний від нуля, то ці вектори утворюють базис у просторі (лінійно незалежні).

Приклад 2. При якому значенні параметра вектори і компланарні ?

Розв’язання. Використовуємо умову компланарності (7.4):
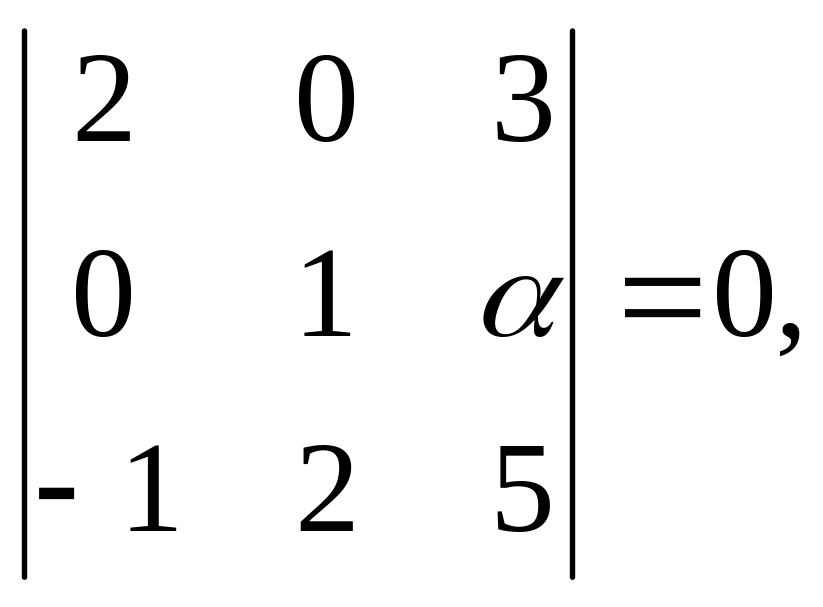