1.6 Обратная матрица.
Если для матрицы
A
существует матрица
,
такая что
(E - единичная матрица), то называется обратной матрицей для матрицы A.
Из данного определения и определения произведения матриц следует, что обратная матрица может существовать только для квадратной матрицы, при этом должна иметь тот же порядок, что и A.
Квадратная
матрица A
называется невырожденной,
если ее определитель не равен нулю:
.
Теорема (об обратной матрице).
Для квадратной невырожденной матрицы
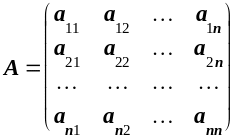
существует и притом единственная обратная матрица , при этом
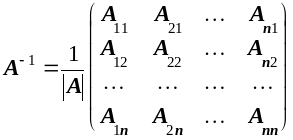
Здесь
-
алгебраические дополнения элементов
определителя матрицы A.
Справедлива и обратная теорема: если для матрицы A существует обратная, то , т. е. A - невырожденная.
Таким образом, для нахождения матрицы, обратной для матрицы A, необходимо:
- вычислить определитель матрицы A и убедиться, что он не равен нулю: ;
- найти алгебраические дополнения элементов определителя матрицы A;
- составить матрицу, строками которой являются алгебраические дополнения элементов соответствующих столбцов определителя исходной матрицы A ;
- умножить полученную
матрицу на число
.
Пример 9. Найти матрицу, обратную для матрицы
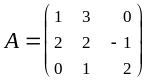
и сделать проверку.
Вычислим
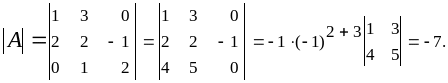
Найдем алгебраические дополнения элементов первого, второго, третьего столбцов определителя матрицы :
Составим обратную матрицу:
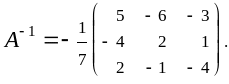
Для проверки, в
соответствии с определением обратной
матрицы, необходимо убедиться, что
выполнено одно из равенств
или
(второе будет следовать из первого).
Вычислим
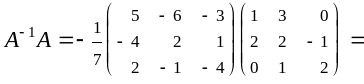
1.7 Ранг матрицы.
Минором k - го порядка матрицы A называется определитель, составленный из элементов, стоящих на пересечении выбранных k строк и k столбцов матрицы A.
Рангом матрицы A r(A) называется наивысший порядок отличных от нуля миноров этой матрицы.
Таким образом, ранг матрицы - натуральное число. Ранг нулевой матрицы принимается равным нулю - у нее нет отличных от нуля миноров. Очевидно, что ранг матрицы не превосходит числа ее строк и числа столбцов.
Пример 10. Найти ранг матрицы
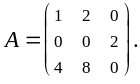
Здесь наивысший
порядок миноров равен 3 - единственным
минором 3-го порядка является определитель
матрицы. Но
,
т. к. 1-я и 3-я строки определителя
пропорциональны (свойство 6). Минор
второго порядка, полученный выделением
1-й и 2-й строки, 1-го и 3-го столбца
Таким образом, r(A) = 2.
Теорема (о ранге матрицы ступенчатого вида).
Ранг матрицы ступенчатого вида равен числу ее ненулевых строк.
Пример 11. Ранг матрицы
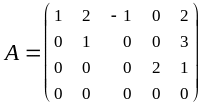
равен 3, т. к. у нее 3 ненулевых строки. Отличный от нуля минор максимального порядка в этой матрице можно выбрать, выделив все ее ненулевые строки, а столбцы выделять так, чтобы получился определитель треугольного вида. В рассматриваемом примере это будет определитель
(выбраны 1-й, 2-й, 4-й столбцы).
Элементарными преобразованиями матрицы называются:
- перестановка двух строк (столбцов) матрицы;
- умножение строки (столбца) на число, отличное от нуля;
- прибавление к строке (столбцу) другой строки (столбца).
Теорема (об элементарных преобразованиях матрицы).
Элементарные преобразования не меняют ранга матрицы.
С помощью элементарных преобразований (при этом можно ограничиться только преобразованиями строк) любую матрицу можно привести к матрице ступенчатого вида. Ранг последней (согласно теореме о ранге матрицы ступенчатого вида) равен числу ненулевых строк и по тереме об элементарных преобразованиях он будет совпадать с рангом исходной матрицы.
Если r(A)=r(B), то матрицы A и B будем называть эквивалентными и обозначать AB.
Пример 12. Найти ранг матрицы
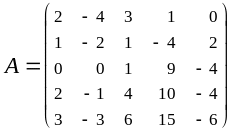
С помощью элементарных преобразований строк будем приводить матрицу к ступенчатому виду.
На первом шаге в первом столбце получим нули во всех строках, кроме первой, оставляя первую без изменения и используя ее для преобразования остальных: 2-ю умножим на -2 и прибавим к ней 1-ю; 3-ю оставим без изменения - на первом месте уже стоит ноль; к 4-й прибавим 1-ю, умноженную на -1; 5-ю умножим на -2 и прибавим к ней 1-ю, умноженную на 3;
A
.
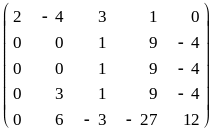
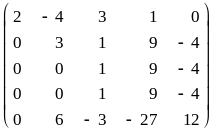В последнем преобразовании переставлены местами 2-я и 4-я строки.
На втором шаге получим нули во 2-м столбце, теперь уже с помощью 2-й строки. Для этого достаточно к 5-й строке прибавить 2-ю, умноженную на -2:
A
.
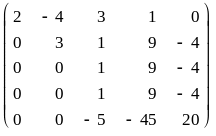Теперь 1-я, 2-я и 3-я строки удовлетворяют требованиям определения матрицы ступенчатого вида. В 4-й и 5-й строках получим нули в 3-м столбце с помощью 3-й строки. Для этого к 4-й прибавим 3-ю, умноженную на -1; к 5-й - третью, умноженную на 5:
A
.
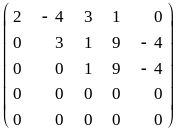Получилась матрица ступенчатого вида, ее ранг - число ненулевых строк - 3, значит и r(A)=3.