6. Показательные и логарифмические

выражения

6.1. Показательная функция, гиперболические

функции

Показательной функцией называется функция

где

Основные свойства показательной функции

1. Область определения:

2. Множество значений:

3. Четность и нечетность: не обладает свойством четности.

4. Периодичность: непериодическая.

5. Нули функции: нулей не имеет.

6. Промежутки знакопостоянства: функция положительна для

7. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.

8. Промежутки возрастания и убывания: если функция возрастает для всех если – убывает для

9. Точки пересечения с осями координат: пересекает ось Оу в точке ось Ох не пересекает.

10. Асимптоты: прямая y = 0 (ось Ох) является горизонтальной асимптотой.

11. График функции для a > 1 изображен на рис. 6.1, для – на рис. 6.2.

Рис. 6.1 Рис. 6.2

Из свойств функции следует: неравенство равносильно неравенствам:

1) если

2) если

Показательная функция с основанием е, где е – иррациональное число е = 2,718281…, называется экспонентой, пишут или

Через показательные выражения с основанием е определяются гиперболические функции.

Гиперболическим синусом называется функция

Основные свойства гиперболического синуса

1. Область определения:

2. Множество значений:

3. Четность и нечетность: нечетная.

4. Периодичность: непериодическая.

5. Нули функции:

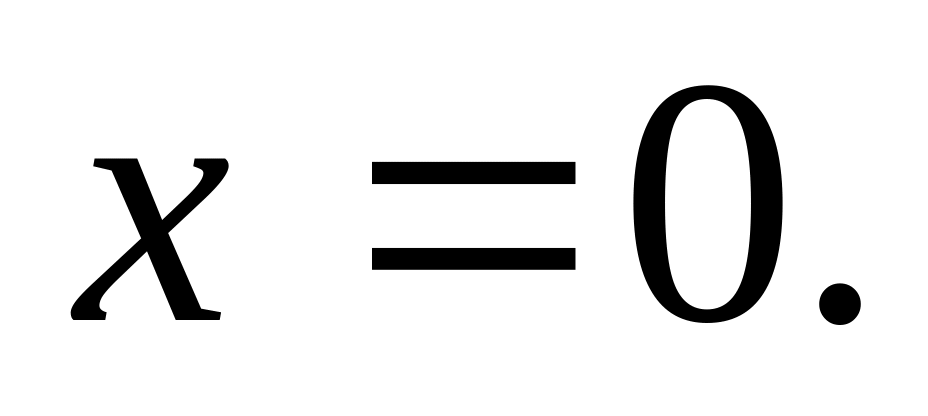
6. Промежутки знакопостоянства: функция отрицательна для положительна – для

7. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.

8. Промежутки возрастания и убывания: функция возрастает для всех

9. Точки пересечения с осями координат:

10. Асимптоты: асимптот не имеет.

11. График функции изображен на рис. 6.3.

Гиперболическим косинусом называется функция

Основные свойства гиперболического косинуса

1. Область определения:

2. Множество значений:

3. Четность и нечетность: четная.

4. Периодичность: непериодическая.

5. Нули функции: нулей не имеет.

6. Промежутки знакопостоянства: функция положительна для

7. Наибольшее и наименьшее значения: наименьшее значение, равное 1, функция принимает при

8. Промежутки возрастания и убывания: функция убывает при возрастает при

9. Точки пересечения с осями координат: пересекает ось Оу в точке ось Ох не пересекает.

10. Асимптоты: асимптот не имеет.

11. График функции изображен на рис. 6.4.

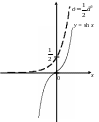
Рис. 6.3 Рис. 6.4

Гиперболические тангенс и котангенс определяются через отношение гиперболических синуса и косинуса.

Гиперболическим тангенсом называется функция

т. е.

Основные свойства гиперболического тангенса

1. Область определения:

2. Множество значений:

3. Четность и нечетность: нечетная.

4. Периодичность: непериодическая.

5. Нули функции:

6. Промежутки знакопостоянства: функция отрицательна для положительна для

7. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.

8. Промежутки возрастания и убывания: функция возрастает для

9. Точки пересечения с осями координат:

10. Асимптоты: имеет горизонтальные асимптоты и

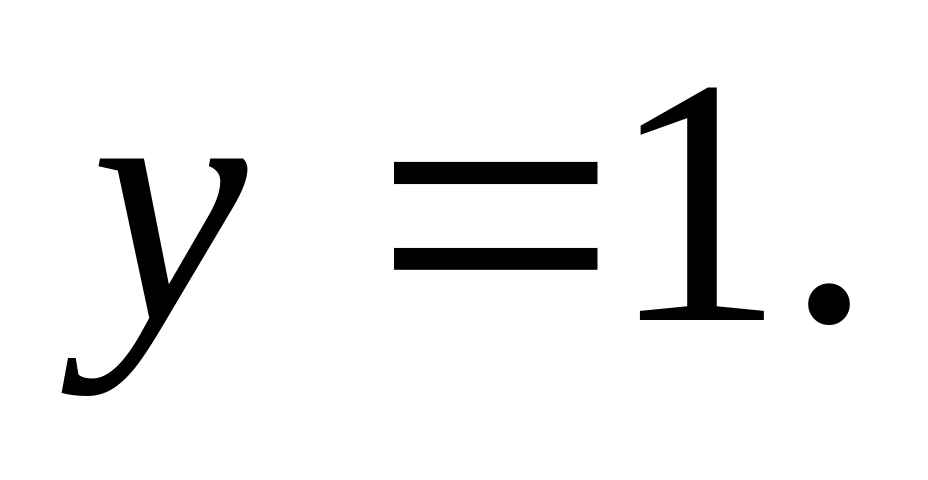
11. График функции изображен на рис. 6.5.

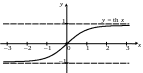
Рис. 6.5

Гиперболический котангенсом называется функция

т. е.

Основные свойства гиперболического котангенса

1. Область определения:

2. Множество значений:

3. Четность и нечетность: нечетная.

4. Периодичность: непериодическая.

5. Нули функции: нулей не имеет.

6. Промежутки знакопостоянства: функция отрицательна для положительна для

7. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.

8. Промежутки возрастания и убывания: функция убывает для

9. Точки пересечения с осями координат: нет.

10. Асимптоты: имеет горизонтальные асимптоты и

11. График функции изображен на рис. 6.6.

Рис. 6.6

Пример 1. Сравнить числа:

1) и 2) и

3) и

Решение. 1) Преобразуем числа к одному основанию:

Так как и функция монотонно возрастает, то следовательно,

2) Преобразуем числа:

Так как и функция монотонно убывает, то следовательно,

3) Преобразуем числа:

Так как и функция монотонно возрастает, то тогда и

Пример 2. Построить график функции:

1) 2)

Решение. 1) Строим график функции

График функции получаем из предыдущего путем смещения его на 3 единицы влево по оси Ох и на 4 единицы вниз по оси Оу.

Для построения графика заданной функции оставляем ту часть графика функции которая лежит над осью Ох и на оси Ох. Ту часть графика, которая расположена ниже оси Ох, отображаем в верхнюю полуплоскость симметрично относительно оси Ох (рис. 6.7).

Рис. 6.7

2) Строим график функции (см. рис. 6.5).

График функции получаем из предыдущего путем смещения его на 2 единицы вниз вдоль оси Оу.

Для построения графика заданной функции оставляем ту часть графика функции которая лежит правее оси Оу и на оси Оу. Часть графика, которая лежит левее оси Оу, отбрасываем, а оставшуюся часть отображаем в левую полуплоскость симметрично оси Оу (рис. 6.8).

Рис. 6.8

Пример 3. Доказать тождество

Решение.

Задания