1.9. Производная функции, заданной параметрически

Пусть функция у от х задана параметрическими уравнениями: , (гл.1, §2, п.2.5). Предположим, что эти функции имеют производные и что функция имеет обратную , которая также имеет производную. Тогда определенную параметрическими уравнениями функцию можно рассматривать как сложную функцию

или .

По правилу (3.7) дифференцирования сложной функции получим:

(3.10)

На основании (3.4) теоремы о производной обратной функции, следует:

или .

Подставляя последнее выражение в равенство (3.10), получаем

. (3.11)

Выведенная формула дает возможность находить производную от функции, заданной параметрически, не находя выражения непосредственной зависимости у от х.

Пример. Найти производную функции, заданной параметрическими уравнениями Согласно (3.11) имеем

1.10. Односторонние производные

Пусть функция в некоторой точке х₀ имеет предел справа. Выражение

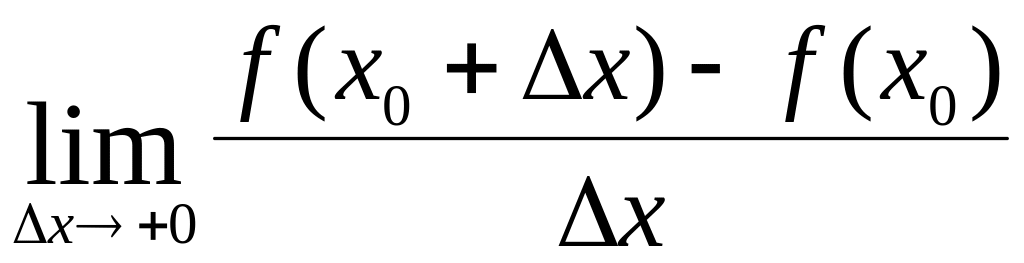
называется правой производной функции и обозначается . Аналогично

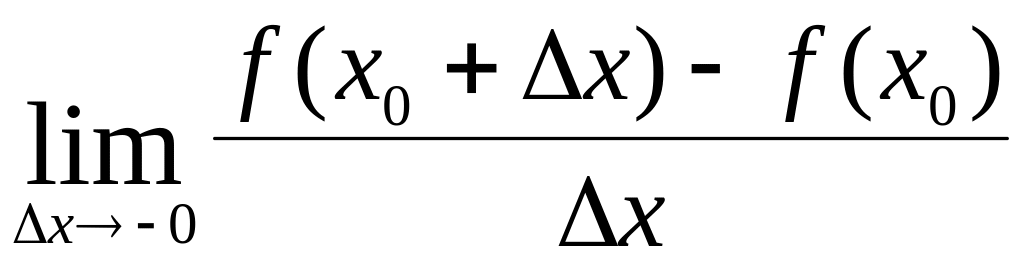
называется левой производной функции и обозначается . Левая и правая производные называются односторонними производными.

Если = , то существует и = = . Если f(x) не определена справа от данной точки, то не существует правой производной в этой точке. Относительно левой производной рассуждения аналогичны.

Наличие односторонних производных геометрически означает наличие в соответствующих точках графика функции односторонних касательных.

Может случиться, что в некоторой точке х₀ существуют оба односторонних предела, не равных между собой. Для графика функции в соответствующей точке будут существовать лишь односторонние касательные, составляющие угол; точка х₀ будет угловой (рис.16,а).

Например, функция у = f(x) = |х| в точке х₀ = 0 не имеет производной, однако существуют односторонние производные. Если Δх > 0, то

Δу = Δх, =

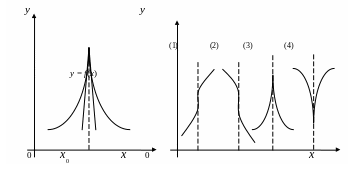
(а) (б)

Рис. 16

Если же Δх < 0, то

Δу = –Δх, =

Начало координат является угловой точкой для графика этой функции, состоящей из биссектрис первого и второго координатных углов.

1.11. Бесконечные производные

Если , то говорят, что функция в этой точке имеет бесконечную производную (и обозначают как обычно). Аналогично устанавливается понятие об односторонней бесконечной производной. Геометрически существование бесконечной производной означает, что касательная к кривой в данной точке перпендикулярна к оси абсцисс Ох (рис.16,б). В случаях (1) и (2) эта производная равна, соответственно +∞ и –∞ (обе односторонние производные совпадают по знаку); в случаях же (3) и (4) бесконечная производная не имеет определенного знака (односторонние производные разнятся знаками).

Пользуясь расширением понятия производной, можно дополнить формулу (3.4) о производной обратной функции указанием, что и в тех случаях, когда равна 0 или ∞, производная обратной функции существует и равна, соответственно, ∞ или 0. Например, так как функция при х = ± имеет производную cos (±) = 0, то для обратной функции х = arcsin у при у = ±1 существует бесконечная производная (именно, ).