364

Глава 6 числовые бесконечные ряды

§1. Определения. Примеры.

Наряду с понятием производной, определенного интеграла важным понятием математического анализа является понятие бесконечного ряда. Взаимное переплетение этих трех понятий обогащает методы математического анализа и позволяет доводить решение задач до получения численного результата.

Определение 1. Пусть, следуя некоторому закону, задана последовательность действительных чисел тогда, соединяя числа этой последовательности между собой знаками плюс, получаем выражение называемое числовым бесконечным рядом

(либо ), (6.1)

числа называются членами (или элементами) бесконечного ряда. Член x_n с индексом n = 1, 2, 3… называется общим членом ряда.

Здесь уместно предостеречь от смешения двух различных понятий, нельзя смешивать арифметическую сумму, то есть сумму конечного числа слагаемых, с понятием ряда содержащего бесконечное число слагаемых. Изучение этой главы покажет, что различие в количестве членов арифметической суммы и ряда (конечное и бесконечное число членов), приводит к тому, что некоторые свойства рядов существенным образом отличаются от соответствующих свойств арифметических сумм. Однако, наряду с этим, множество свойств арифметических сумм можно распространить на некоторые типы рядов. Обо всем этом речь впереди.

Заметим, что в средней школе учащийся встречается с частными случаями понятия ряда дважды.

Во-первых, при изучении бесконечных десятичных дробей.

Например, . Здесь в скрытом виде присутствует понятие ряда. Действительно, последнее равенство можно записать следующим образом

.

Аналогичное замечание можно сделать и по поводу других бесконечных десятичных дробей.

Во-вторых, при изучении убывающей геометрической прогрессии, то есть геометрических прогрессий, у которой знаменатель прогрессии q, удовлетворяет неравенству −1 < q < +1. Рассматривалась бесконечная сумма членов этой прогрессии (т.е. числовой ряд) и было доказано, что

.

Теперь перейдем к изучению ряда с общей точки зрения. Образуем последовательность

(6.2)

усеченных сумм ряда (6.1) определяя элементы этой последовательности при помощи равенств , ,…, .

Заметим, что каждый элемент последовательности (6.2) есть конечная арифметическая сумма, содержащая n слагаемых ряда, в дальнейшем такие суммы мы будем называть усеченной суммой ряда порядка n.

Таким образом, каждому ряду ставится в соответствие единственная последовательность (6.2) – последовательность его усеченных сумм. Обратно, если задана последовательность (6.2), то с ее помощью можно восстановить ряд (6.1). Для этого нужно показать, как найти каждый член ряда (6.1). Прежде всего, имеем _. Далее, из S₂ вычитая S₁, найдем _. Продолжая эту процедуру, найдем каждый член ряда (6.1) , где n = 3,4,5,….

Отсюда следует, что если известна последовательность (6.2), то можно восстановить ряд, для которого (6.2) есть последовательность его усеченных сумм. Поэтому задание ряда (6.1) равносильно заданию последовательности (6.2). Замечаем, что при число членов в усеченной сумме неограниченно увеличивается и потому делается «похожей» на порождающий ее ряд (6.1). Это замечание дает повод к такому определению.

Определение 2. Числовой бесконечный ряд называется сходящимся, если его последовательность усеченных сумм имеет конечный предел . Число S называется суммой ряда (6.1) и в этом случае пишут

(или ). (6.3)

Все остальные ряды называются расходящимися и они суммы не имеют.

Все расходящиеся ряды удобно разбить на два типа.

Если , то расходящийся ряд (6.1) в этом случае будем называть собственно расходящимся. Если же не существует, то в этом случае расходящийся ряд (6.1) называется осциллирующим или колеблющимся. Далее будут приведены примеры сходящихся, собственно расходящихся и осциллирующих рядов. Уже теперь, в самом начале изложения теории рядов видно существенное различие между арифметической суммой и рядом. Арифметическая сумма всегда имеет числовое значение, но ряду можно придать числовое значение, то есть сумму, лишь тогда когда он является сходящимся.

Если ряд (6.1) сходится, и справедливо равенство (6.3), то это означает, что приближенное равенство может быть сделано сколь угодно точным при достаточно большом значении n. Это замечание имеет важное практическое значение. Если сумма сходящегося ряда неизвестна, то ее можно вычислить с любой наперед заданной степенью точности по формуле

(6.4)

или, другими словами, заменяем ряд его усеченной суммой порядка n, отбрасывая все члены ряда, начиная с . Число n, оставляемых членов в выражении (6.4) зависит от нужной степени точности.

Далее рассмотрим примеры числовых бесконечных рядов.

Пример 1. Исследуем ряд

. (6.5)

Составим n-ую усеченную сумму .

Займемся преобразованием каждого слагаемого в . Имеем легко проверяемое равенство и полагая здесь n равным 1, 2,…, придадим следующий вид

.

После этого, раскрывая скобки и уничтожая равные слагаемые, имеющие разные знаки, получим . Значит .

Следовательно, ряд (6.5) сходится и имеет сумму равную 1.

Пример 2. Исследуем ряд, который называется гармоническим

(6.6)

Начнем с подготовительных преобразований. Ранее было показано (гл.1, §5, п.5.7), что монотонно возрастающая последовательность 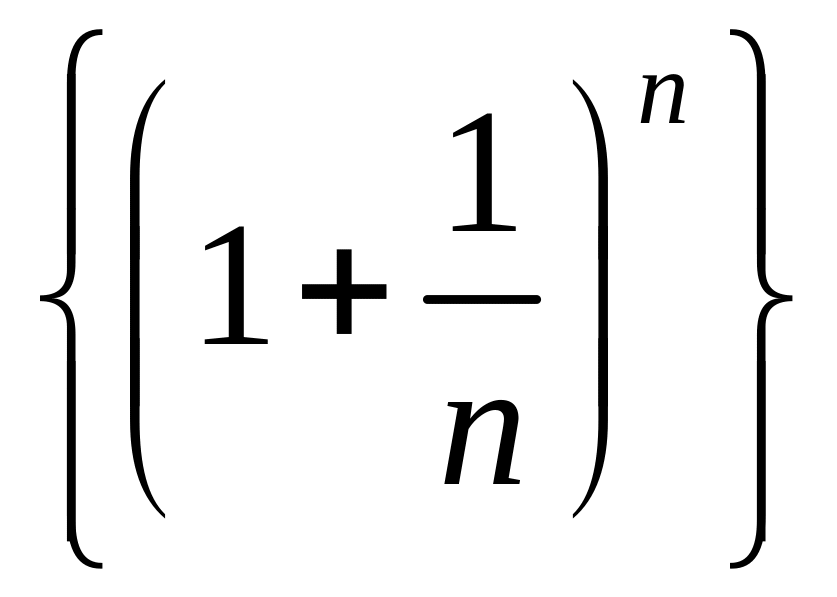стремится к пределу e. Отсюда заключаем, что при любом натуральном n справедливо неравенство 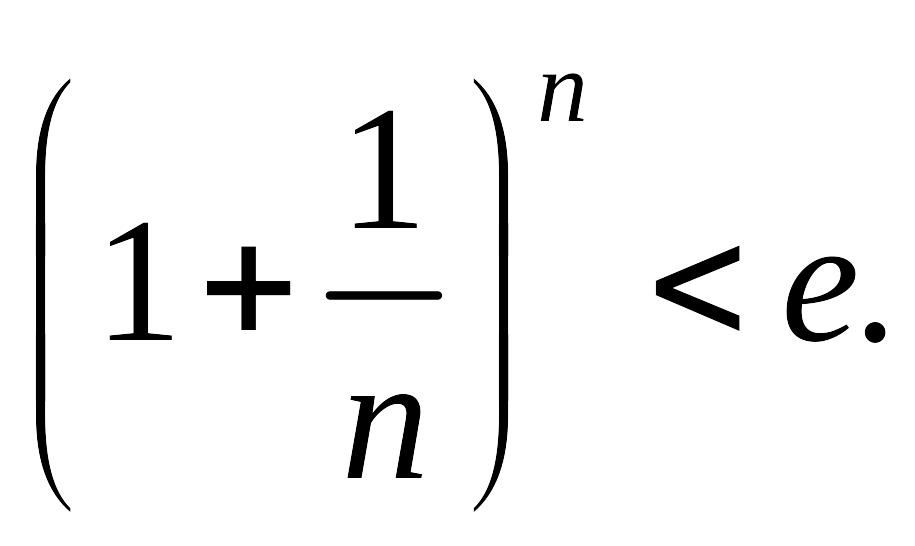Логарифмируя это неравенство по основанию e, имеем . Отсюда, находим, что . Полагая в этом неравенстве n равным 1, 2,…, n, получаем , ,…, .

Складывая полученные n неравенств, находим .

Отсюда после упрощений получаем

(6.7)

причем это неравенство справедливо при любых натуральных n.

Левая часть неравенства (6.7) представляет собой усеченную сумму ряда (6.6) порядка n, следовательно

. (6.8)

Но правая часть (6.8) при стремится к + , а поэтому и подавно . Это значит, что гармонический ряд есть собственно расходящимся.

Пример 3. Исследуем ряд

. (6.9)

Составляя для него усеченные суммы, найдем и вообще нечетная усеченная сумма, а четная усеченная сумма . Последовательность усеченных сумм, следующая 1,0,1,0,…,1,0,… и отсюда заключаем, что она не имеет предела, то есть не существует. Значит ряд (6.9) является осциллирующим рядом.