
- •Глава 7 функциональные ряды
- •§1. Сходящиеся и равномерно сходящиеся функциональные ряды
- •1.1. Определение функционального ряда и его сходимости
- •1.2. Равномерно сходящиеся функциональные ряды
- •1.3. Достаточный признак Вейерштрасса (равномерной сходимости функционального ряда).
- •§2. Непрерывность суммы функционального ряда
- •§3. Интегрирование и дифференцирование Функционального ряда
- •3.1. Интегрирование функционального ряда
- •3.2. Дифференцирование функционального ряда
- •§4. Степенные ряды
- •4.1. Сходимость степенного ряда
- •4.1.1. Теорема Абеля
- •4.1.2. Интервал и радиус сходимости степенного ряда
- •4.1.3. Определение радиуса сходимости степенного ряда
- •4.1.4. Равномерная сходимость степенного ряда
- •4.2. Дифференцирование степенного ряда
- •4.3. Интегрирование степенного ряда
- •§5. Ряды Тейлора и Маклорена. Понятие аналитической функции
- •5.1. Аналитические функции
- •5.2. Разложение в ряд Маклорена функции ex
- •5.3. Разложение в ряд Маклорена функций sin X, cos X
- •5.5. Разложение в ряд Маклорена функции arctgx
- •§6. Ряды с комплексными членами
- •6.1. Предел последовательности комплексных чисел
- •6.2. Сходимость ряда комплексных чисел
- •6.3. Степенной ряд комплексных чисел
- •6.4. Разложение показательной функции ez комплексного переменного z в степенной ряд. Формулы Эйлера
- •Упражнения
5.5. Разложение в ряд Маклорена функции arctgx
Здесь исходной будет сходящаяся в интервале (–1,+1) геометрическая прогрессия
![]() . (7.98)
. (7.98)
Пусть x – произвольная точка из интервала (–1,+1): –1 < x <+1. Рассмотрим сегмент [0,x] (или [x,0], если x < 0), который целиком лежит в интервале (–1,+1) и потому, равенство (7.98) можно почленно интегрировать.
В результате несложных интегрирований получаем
![]() .
(7.99)
.
(7.99)
Ряд в правой части (7.99), также как и исходный ряд в правой части (7.98), имеет радиус сходимости равный единице. Поэтому вне сегмента [–1,+1], разложение (7.99) не действительно. Остается проверить справедливость (7.99) в точках x = +1 и x = –1. В силу нечетности обеих частей равенства (7.99) достаточно установить его справедливость при x = +1.
Заменяя в разложении (7.88) x через x2, получаем
![]() . (7.100)
. (7.100)
Интегрируя почленно в сегменте [0,1] последнее равенство, находим
![]() .
.
Отсюда, после вычисления интегралов имеем
![]() . (7.101)
. (7.101)
Исследуем остаточный член формулы (7.101)
![]() (7.102)
(7.102)
Из
последнего равенства получаем
![]() .
.
Отсюда следует
. (7.103)
Таким образом, в точке х = +1 функция arctg x аналитическая и для нее в этой точке имеет место разложение
![]() . (7.104)
. (7.104)
Из (7.104) следует, что разложение (7.99) справедливо при x = +1. В силу нечетности левой и правой части (7.99) справедливость (7.104), а, следовательно, и разложения (7.99) распространяется и на точку x = –1.
Итак,
равенство (7.99) выполняется при
![]() .
.
Рассмотрим, как можно использовать разложение (7.99) для вычисления числа π. Для этого обозначим через φ такой угол, что
![]() (7.105)
(7.105)
После этого найдем tg 2φ и tg 4φ:
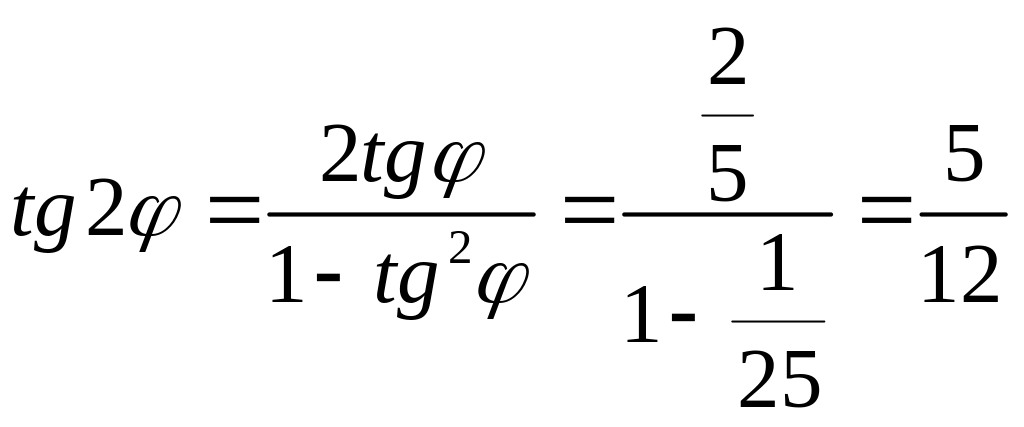 ;
;
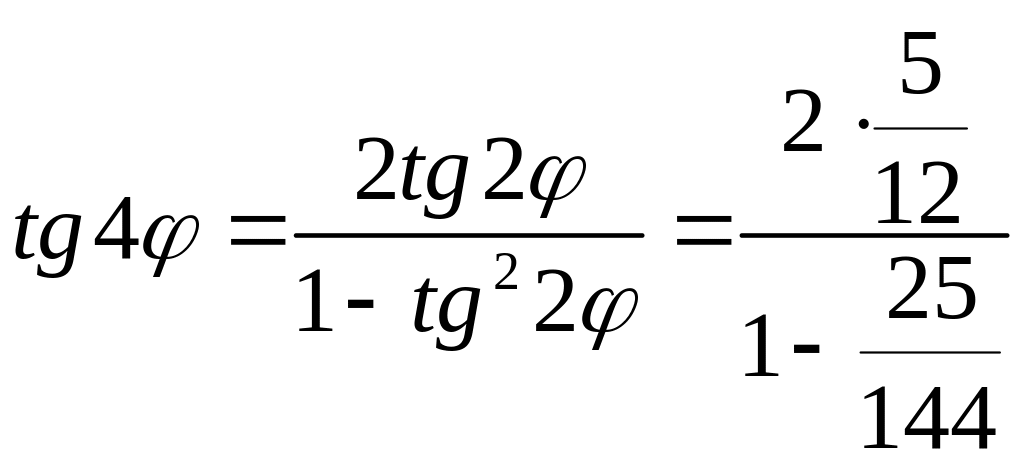
![]() .
.
Для
tg 4φ
получилось значение, которое мало
отличается от единицы. Поэтому 4φ
незначительно отличается от
![]() .
Обозначим разницу
.
Обозначим разницу
![]() через
через
![]() :
:
![]() (7.106)
(7.106)
и вычислим tg ψ
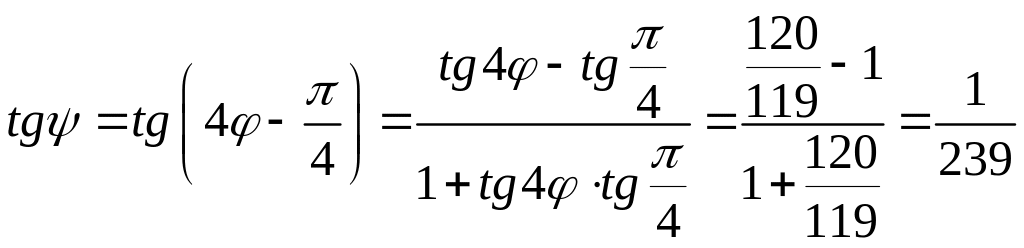 . (7.107)
. (7.107)
Из
(7.105) и (7.107) находим
![]() .
.
Подставляя эти значения в (7.106), получаем
![]() . (7.108)
. (7.108)
Полагая
в (7.99)
![]() и
и
![]() ,
находим
,
находим
![]() , (7.109)
, (7.109)
![]() . (7.110)
. (7.110)
Отметим, что ряды в правых частях равенств (7.109) и (7.110) быстро сходятся и, следовательно, их очень удобно использовать для приближенного вычисления. Подставляя эти ряды в равенство (7.108), получим формулу для приближенного вычисления числа π
![]() . (7.111)
. (7.111)
Если в формуле (7.111) принять в расчет только выписанные члены рядов, то допущенную при таком вычислении ошибку ρ легко оценить.
По
следствию из принципа Лейбница, при
вычислении сумы ряда (7.109)
с помощью первых четырех членов ряда
допускается ошибка, которая меньше, чем
первый отброшенный член
![]() .
При вычислении суммы ряда (7.110),
когда ее полагают равной первым двум
членам, возникает ошибка, которая меньше,
чем третий отброшенный член
.
При вычислении суммы ряда (7.110),
когда ее полагают равной первым двум
членам, возникает ошибка, которая меньше,
чем третий отброшенный член
![]() .
.
На основании изложенного ошибка ρ меньше, чем
![]() .
.
Следовательно,
ошибка при вычислении числа π
по приближенной формуле
![]() составляет
0
<
ρ
<·10−6.
Если в этой формуле вычисление каждого
слагаемого вести до седьмого десятичного
знака, то получим,
составляет
0
<
ρ
<·10−6.
Если в этой формуле вычисление каждого
слагаемого вести до седьмого десятичного
знака, то получим,
![]() причем верными являются, лишь первые
пять десятичных знаков.
причем верными являются, лишь первые
пять десятичных знаков.
5.6. Разложение в ряд Маклорена функции (1+x)α
Для разложения в ряд Маклорена функции
![]() (7.112)
(7.112)
где α – произволное действительное число будем пользоваться формулой Маклорена с остаточным членом Rn+1(x) в форме Коши (глава 3, §5, п.5.2, формула (3.50), при условии, что х0 = 0)
![]() , (7.113)
, (7.113)
где 0 < θ < 1. Найдем последовательные производные функции (7.112)
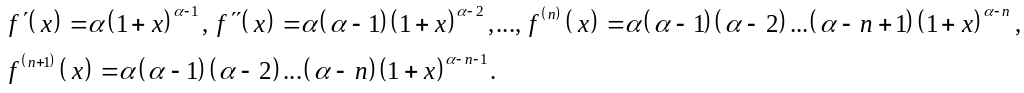
Отсюда получаем
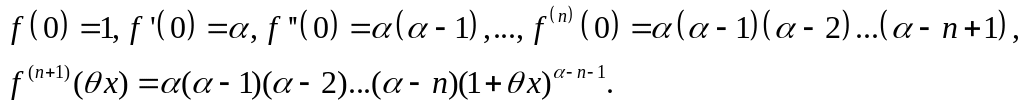
Подставляя найденные значения в (7.113), приходим к равенству
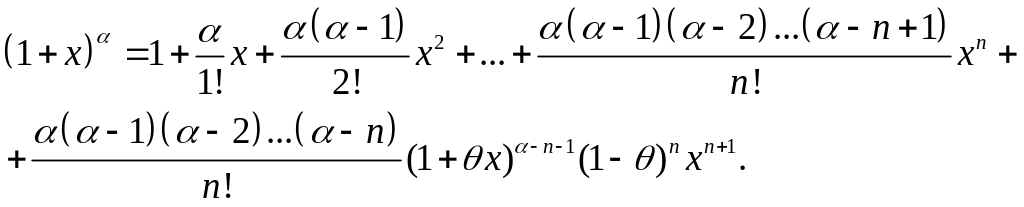 (7.114)
(7.114)
Если α есть натуральное число: α = n, то остаточный член в (7.114), содержащий множитель α – n, обращается в нуль и в этом случае равенство (7.114) превращается в бином Ньютона
![]()
Поэтому в дальнейшем полагаем, что α ≠ 0, 1, 2,… и исследование равенства (7.114) для этих α начнем с определения радиуса сходимости R степенного ряда
![]() . (7.115)
. (7.115)
Для
этого применим формулу
![]() .
.
Здесь
![]()
![]() .
.
Значит
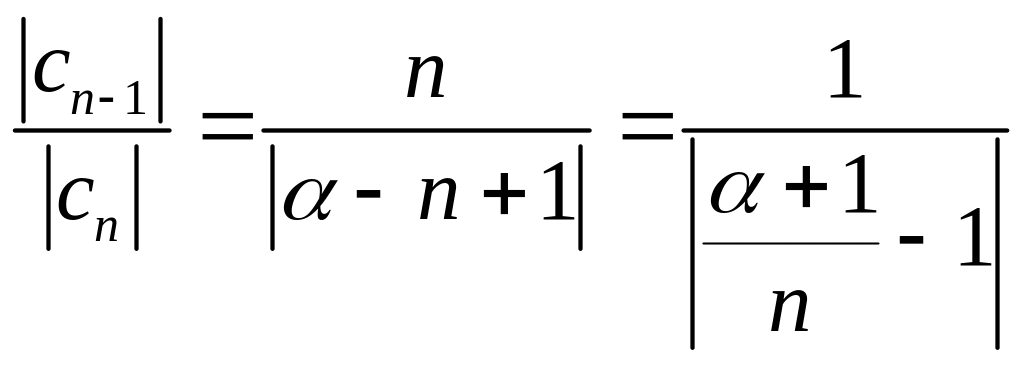 и, следовательно,
и, следовательно,
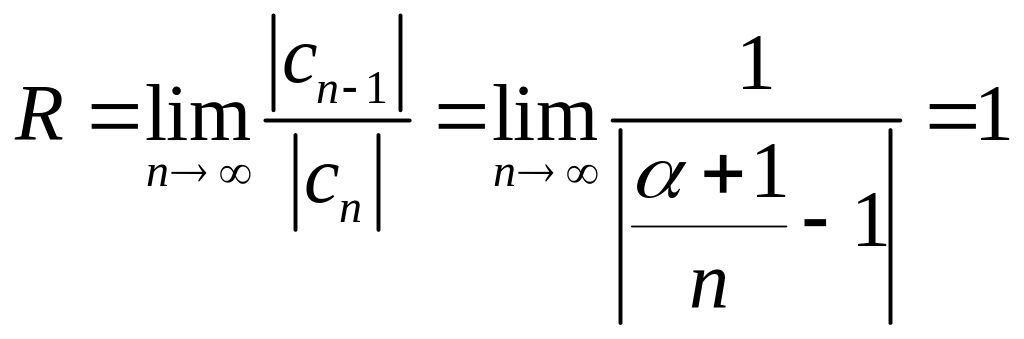 .
.
Таким
образом, степенной ряд (7.115) сходится
при –1
<
x
< +1
и расходится при
![]() .
Поэтому в дальнейшем считаем
.
Поэтому в дальнейшем считаем
–1 < x < +1. (7.116)
Для исследования остаточного члена в равенстве (7.114)
![]() где 0 <
θ
< 1,
где 0 <
θ
< 1,
представим его несколько иначе
![]() . (7.117)
. (7.117)
Теперь
рассмотрим по отдельности поведение
всех трех сомножителей в правой части
(7.117):
![]()
![]() и
и
![]() при n→+∞.
при n→+∞.
Радиус сходимости степенного ряда (7.115) не зависит от величины параметра α, поэтому, если в (7.115) заменить α через α – 1, то степенной ряд
![]() (7.118)
(7.118)
также имеет радиус сходимости равный 1. Это означает, что для всех х в интервале –1 < x <+1 общий член ряда (7.118) при n → +∞ имеет своим пределом число нуль
![]() . (7.119)
. (7.119)
При
соблюдении неравенства (7.116) имеем
![]() и отсюда
и отсюда
![]() .
.
Множитель αx(1+θx)α-1 остаточного члена (7.117) зависит от n, так как θ зависит и от x и от n. Но этот множитель ограничен, так как при любых значениях n он находится между величинами αx и αx(1+x)α-1, которые от n не зависят.
Таким
образом, первый множитель остаточного
члена Rn+1(x)
в формуле (7.117) для всех х
из
интервала (–1,1) при n→+∞
в силу (7.119) имеет своим пределом нуль,
а второй и третий множитель ограничены.
Поэтому для всех х
из
интервала (–1,1) выполняется предельное
равенство
![]() .
.
Следовательно, функция (7.112) в точке х = 0 аналитическая и для нее в интервале (–1,1) справедливо разложение
![]() . (7.120)
. (7.120)
Ряд в правой части (7.120) называется биномиальным рядом.
Рассмотрим частные случаи разложения функций с использованием биномиального ряда.
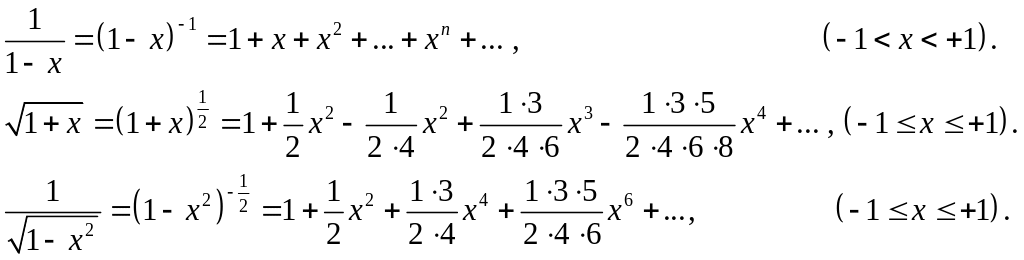
Интегрируя последнее разложение в сегменте [0,x], получаем
![]() .
.
В заключение приводится таблица, показывающая характер сходимости биномиального ряда на концах интервала сходимости.
|
х = –1 |
|
х = +1 |
α ≥ 0 |
АБСОЛЮТНО СХОДИТСЯ |
α ≥ 0 |
АБСОЛЮТНО СХОДИТСЯ |
α <0 |
РАСХОДИТСЯ |
–1<α<0 |
НЕАБСОЛЮТНО СХОДИТСЯ |
|
|
α ≤ –1 |
РАСХОДИТСЯ |
Биномиальный
ряд, в частности, может быть использован
для вычисления корней с любой наперед
заданной степенью точности. Пусть,
например, нужно вычислить
![]() .
Последовательно получаем
.
Последовательно получаем
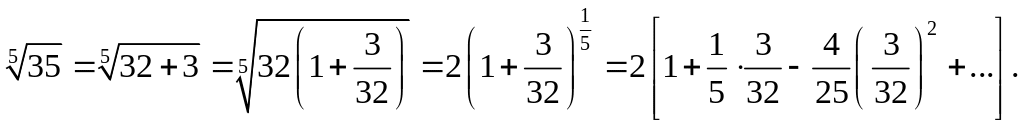
Беря нужное число членов получившегося ряда, смотря по требуемой степени точности, вычисляем приближенное значение .
