Примеры решения типовых задач
Пример 1. Решить ЛНДУ с постоянными коэффициентами
.
Решение. В данном уравнении правая часть не является функцией вида (8.4). Поэтому метод неопределенных коэффициентов здесь не подходит. Воспользуемся методом вариации.
Для начала запишем однородное ДУ, составим соответствующее для него характеристическое уравнение и найдем его корни:
.
Следовательно, общее решение однородного ДУ имеет вид
.
Тогда общее решение ЛНДУ будем искать в виде
.
Составим систему уравнений (8.4.)
Для решения этой системы воспользуемся методом Крамера. Найдем определители второго порядка:
;
;
.
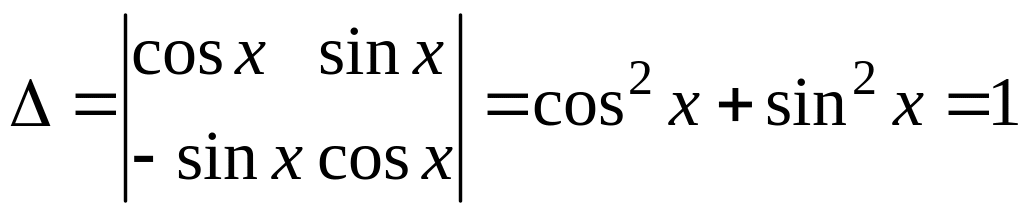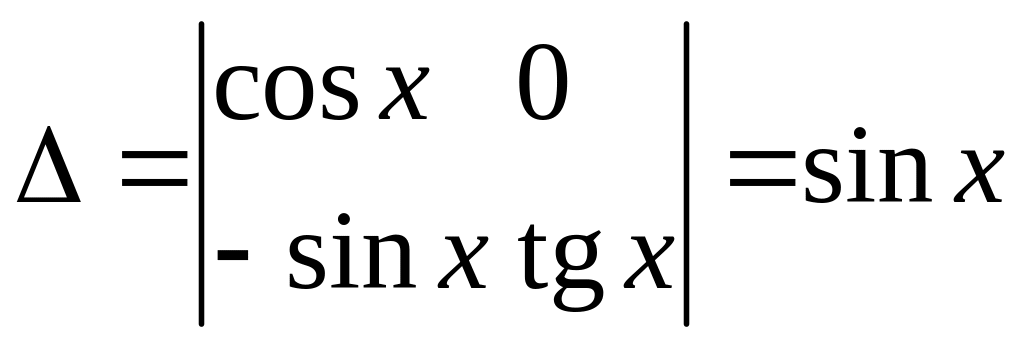Найдем неизвестные:
;
.
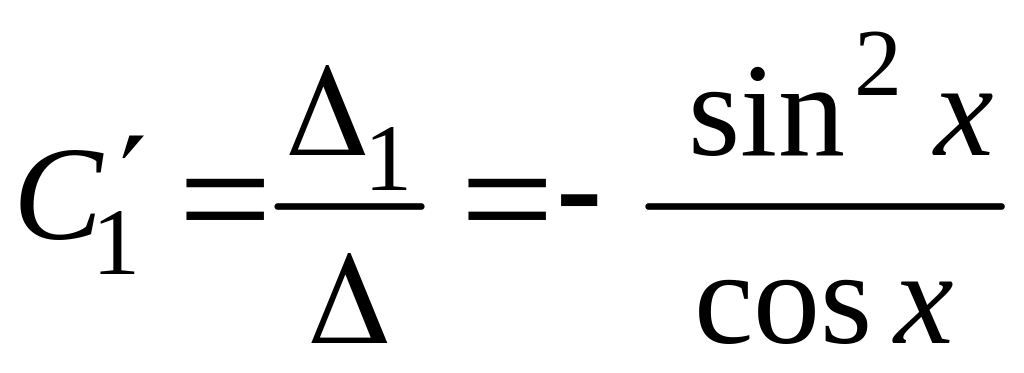Откуда
;
.
Таким образом, общее решение исходного уравнения
.
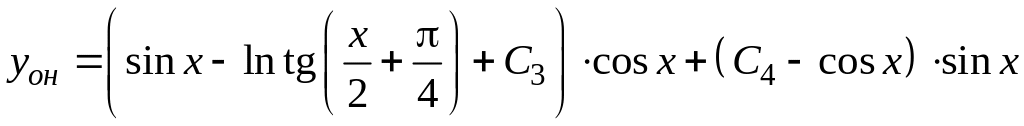Так
как константы
и
в получившемся решении не встречаются,
то константы
и
можно перенумеровать
.
Тогда решение примет вид:
.
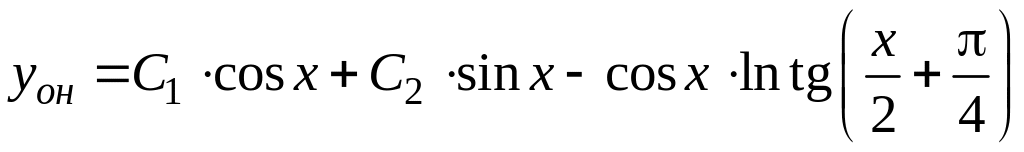Пример 2. Записать вид частного решения уравнения
,
где
а)
;
б)
;
в)
;
г)
;
д)
.
Решение.
Запишем ЛОДУ, составим для него
характеристическое уравнение и найдем
его корни:
.
а)
.
Сравниваем данную функцию с формулой
(8.4), делаем вывод, что
.
Так как число
не является корнем характеристического
уравнения ЛОДУ, следовательно, его
кратность равна нулю, т.е.
.
Так как
и можно полагать, что
,
то
.
Подставляя все найденное в формулу
(8.5), получаем, что частное решение
запишется в виде:
.
б) . Воспользуемся таблицей, имеем второй случай, когда правая часть имеет вид:
,
где
.
Число
является корнем кратности 2
характеристического уравнения. Тогда
частное решение запишем в виде:
.
в)
.
Так как
является корнем кратности
2
характеристического уравнения, то
.
Так как
– многочлен второй степени, то частное
решение имеет вид:
.
г)
.
Функция
имеет вид (8.4), где
,
поэтому
.
Т. к. число
не является корнем характеристического
уравнения, то, подставив все найденные
значения в формулу (8.5), получаем
.
д) . Имеем:
– не
является корнем характеристического
уравнения. Многочлены
– соответственно многочлены второй и
нулевой степени, значит, многочлены
будут иметь вторую степень, так к
.
Решение имеет вид:
.
Пример
3. Найти
частное решение уравнения
,
удовлетворяющее начальным условиям:
.
Решение.
Характеристическое уравнение
имеет корни
.
Значит общее решение соответствующего
однородного уравнения имеет вид
.
Запишем число
(
),
то
.
В данном случае
– многочлен первой степени (
).
Поэтому частное решение данного уравнения
ищем в виде:
.
Найдем
и
:
,
Подставим , и в исходное уравнение, получим:
.
Приравниваем коэффициенты при одинаковых неизвестных в левой и правой частях уравнения, получаем систему двух уравнений с двумя неизвестными:
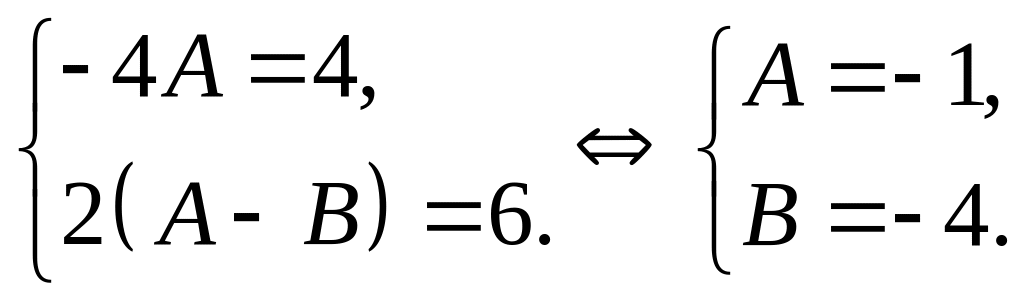
Подставляя
A
и B
в выражение для
,
получаем частное решение данного
уравнения
.
Так как общее решение ЛНДУ есть сумма
и
,
т.е.
,
то для данного уравнения оно имеет вид:
.
Найдем
частное решение. Для этого найдем
производную
.
Составим систему двух уравнений с двумя
неизвестными, учитывая, что
:
Итак, искомое частное решение имеет вид:
.
Пример 4. Найти общее решение уравнения
.
Решение.
Характеристическое уравнение имеет
корни
,
поэтому общее решение однородного
уравнения имеет вид:
.
Используя формулы тригонометрии, преобразуем правую часть уравнения:
,
т.е.
.
Правая часть неоднородного дифференциального уравнения представляет сумму двух функций специального вида:
.
Решим отдельно два уравнения.
а) частное решение неоднородного уравнения:
будем искать в виде:
.
Подставляя
эту функцию в уравнение, находим:
,
поэтому
.
б)
если
,
то в этом случае
,
и так как
.
Тогда
частное решение имеет вид:
.
Дифференцируя и подставляя в уравнение, получаем:
.
Приравниваем многочлены, стоящие перед одноименными тригонометрическими функциями в левой и правой частях уравнения, получаем:
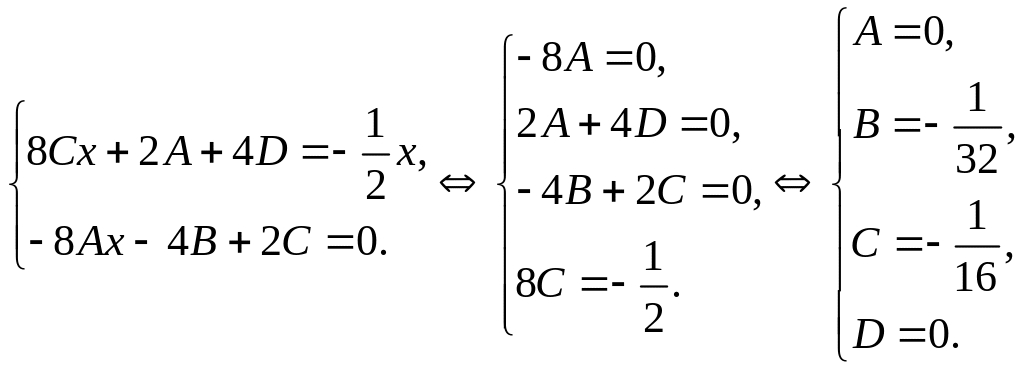
Получаем
.
Объединяя полученные результаты, получаем общее решение исходного уравнения:
.
Пример
5. Найти общее
решение уравнения
.
Решение.
Характеристическое уравнение
или
имеет корни
.
Получили
три простых корня: один действительный
и два комплексно-сопряженных
.
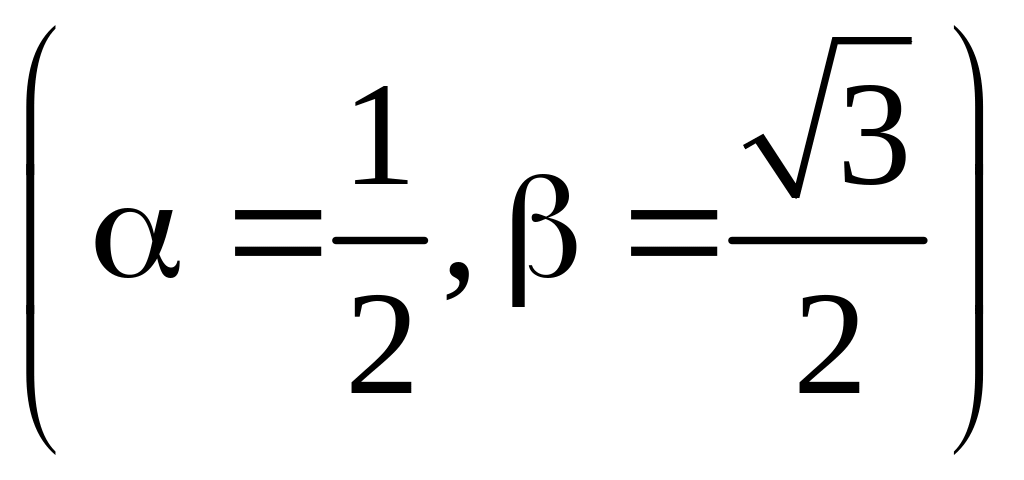С учетом формул (7.3) и (7.5) общее решение
исходного ДУ имеет вид:
.
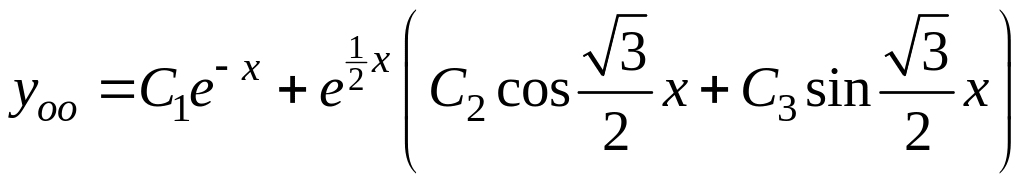Так
как
,
то в данном случае
;
поскольку такого у корня характеристического
уравнения нет, то
.
Многочлен
имеет степень
,
следовательно,
также является многочленом второй
степени и имеет вид:
.
Поэтому частное решение неоднородного
уравнения следует искать в виде:
.
Подставляя эту функцию в исходное уравнение, получаем:
,
поделим
обе части на
:
.
Приравниваем коэффициенты при неизвестных в одинаковой степени, получаем:
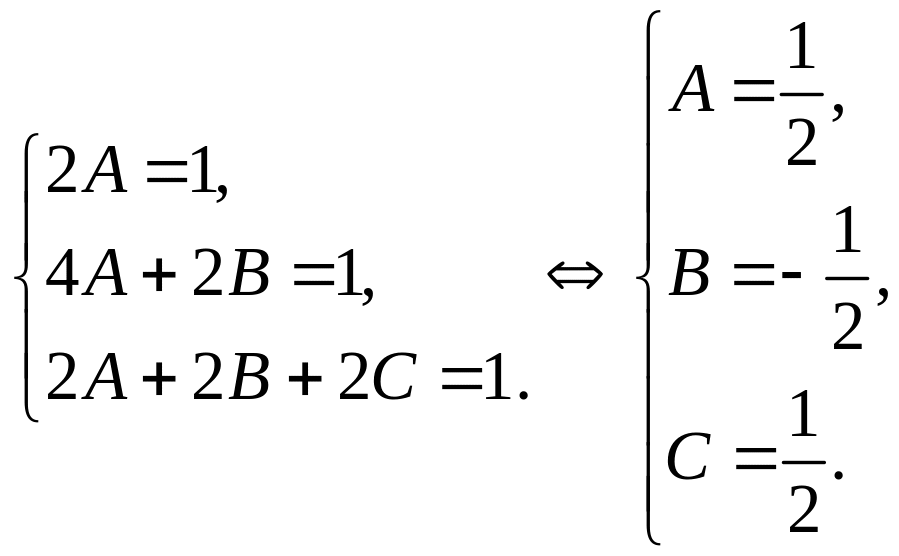
Следовательно, частное решение данного уравнения имеет вид:
.
Объединяя полученные результаты, приходим к выводу, что общее решение исходного уравнения имеет вид:
.
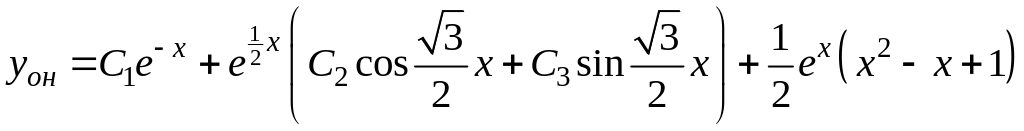