
- •9. Дифференциальные уравнения
- •9.1. Дифференциальные уравнения первого порядка Краткие теоретические сведения
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •9.2. Уравнения с разделяющимися переменными Краткие теоретические сведения
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •9.3. Однородные дифференциальные уравнения Краткие теоретические сведения
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •9.4. Линейные дифференциальные уравнения первого порядка. Уравнение я. Бернулли Краткие теоретические сведения
- •Метод и. Бернулли
- •Метод Лагранжа (метод вариации произвольной постоянной)
- •Уравнение я. Бернулли
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •Интегрирующий множитель
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •9.6. Дифференциальные уравнения второго и более высоких порядков, допускающие понижение порядка Краткие теоретические сведения
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •9.7. Линейные однородные уравнения с постоянными коэффициентами (лоду) Краткие теоретические сведения
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •9.8. Линейные неоднородные уравнения с постоянными коэффициентами второго и более высоких порядков (лнду) Краткие теоретические сведения
- •Метод вариации произвольных постоянных (метод Лагранжа)
- •Метод неопределенных коэффициентов
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •9.9. Приложение дифференциальных уравнений в экономике Краткие теоретические сведения
- •Примеры решения типовых задач
- •Задачи для самостоятельной работы
Задания для самостоятельной работы
n9.5. Решить ДУ с разделяющимися переменными:
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
ж)
|
з)
|
n9.6. Найти решение задачи Коши для указанных ДУ:
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
ж)
|
з)
|
Ответы
9.3. Однородные дифференциальные уравнения Краткие теоретические сведения
К уравнениям с разделяющимися переменными приводятся однородные ДУ первого порядка.
Определение.
Функция
![]() называется однородной
функцией n-го
порядка
(измерения) относительно аргументов
и
,
если при умножении каждого ее аргумента
на произвольный множитель
называется однородной
функцией n-го
порядка
(измерения) относительно аргументов
и
,
если при умножении каждого ее аргумента
на произвольный множитель
![]() вся функция умножается на
вся функция умножается на
![]() ,
т.е. равенство
,
т.е. равенство
![]()
справедливо
для любого![]() ,
при котором функция
,
при котором функция
![]() определена,
определена,
![]() .
.
Например,
функция
![]() есть однородная функция третьего
порядка, так как
есть однородная функция третьего
порядка, так как
![]() .
.
Функция
будет однородной
нулевого порядка, если
![]() ,
т.е. выполняется равенство
,
т.е. выполняется равенство
![]() . (3.1)
. (3.1)
Определение. Дифференциальное уравнение
![]() (3.2)
(3.2)
называется однородным, если функция есть однородная функция нулевого порядка.
Однородное ДУ (3.2) можно переписать в виде:
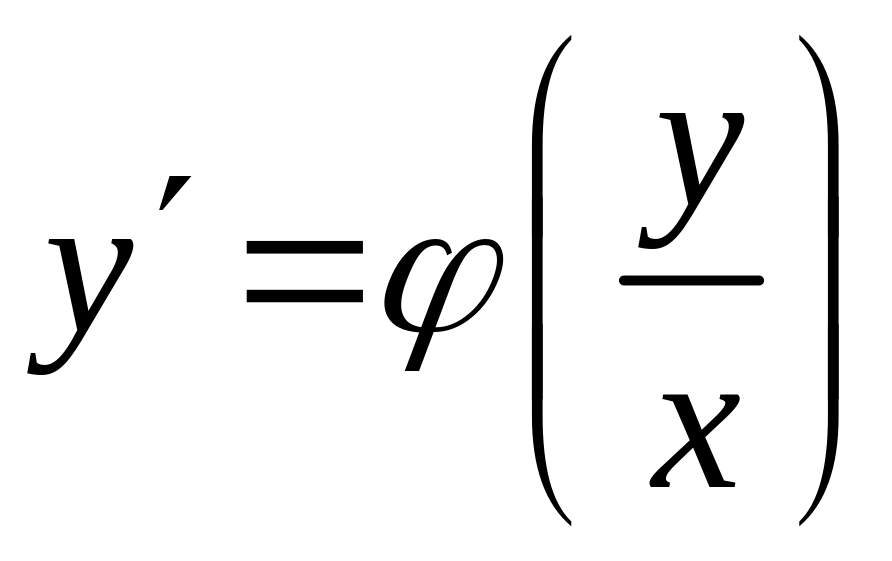 .
.
Действительно,
так как функция
– однородная функция нулевого порядка,
то уравнение (3.2) можно записать в виде
![]() .
.
Положив
![]() ,
получаем:
,
получаем:
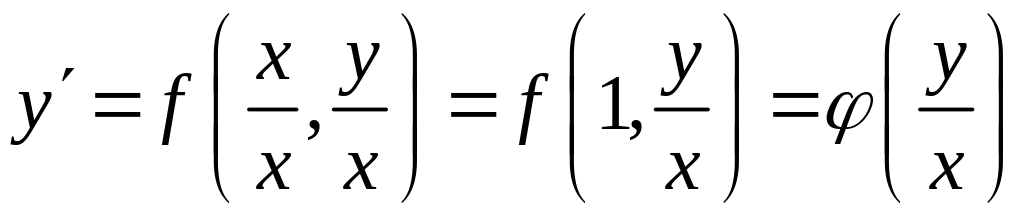 .
.
Следовательно, уравнение (3.2) сводится к уравнению с разделяющимися переменными с помощью замены переменной (подстановкой)
![]() или
или
![]() ,
тогда
,
тогда
![]() ,
,
где
– есть функция переменной
,
т.е.
![]() :
:
![]() .
.
Однородное уравнение часто задается в дифференциальной форме:
. (3.3)
Оно будет однородным в том и только том случае, если и – однородные функции одного и того же порядка, т.е.
![]() и
и
![]() .
.
Действительно, переписав его в нормальной форме:
 ,
,
легко видеть, что – однородная функция нулевого порядка, так как
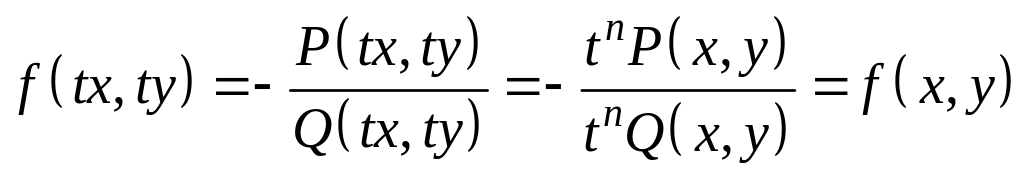 .
.
Замечание.
Уравнение вида
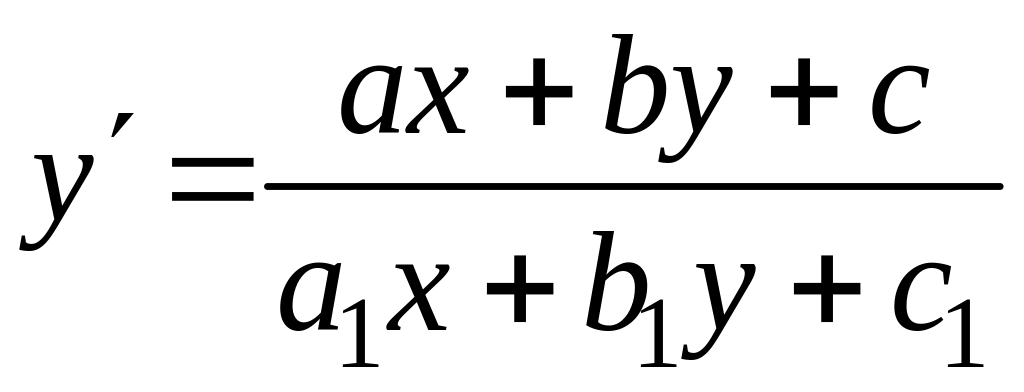 ,
где
,
где
![]() – числа,
приводится к однородному или с
разделяющимися переменными. Для этого
вводятся новые переменные
– числа,
приводится к однородному или с
разделяющимися переменными. Для этого
вводятся новые переменные
![]() и
и
![]() ,
положив
,
положив
![]() ,
где
и
,
где
и
![]() – числа, которые подбирают так, чтобы
уравнение стало однородным.
– числа, которые подбирают так, чтобы
уравнение стало однородным.
Примеры решения типовых задач
Пример 1. Найти все решения ДУ
![]() .
.
Решение. Запишем данное ДУ в форме (3.2)
 .
.
Проверим
функцию
 на однородность нулевого порядка:
на однородность нулевого порядка:
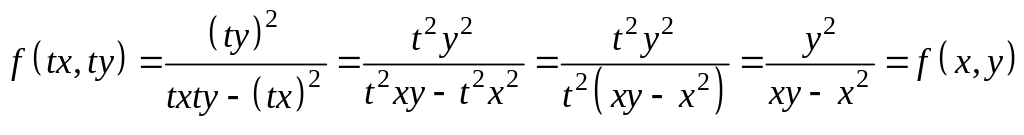 .
.
Из проверки видно, что данное уравнение действительно является однородным. Сделаем замену , . Тогда:

 .
.
Получившееся после преобразований ДУ – есть ДУ с разделяющимися переменными.
Разделяя переменные, последовательно находим:
![]() ,
,
![]()
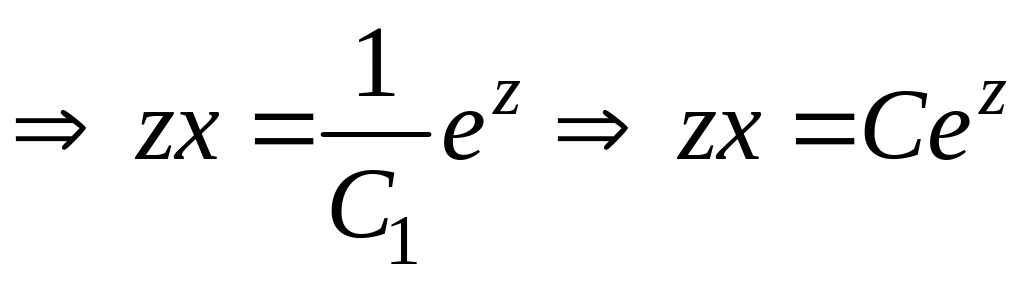 .
.
Сделаем
обратную замену, т.е. в последнее выражение
вместо
подставим значение
![]() .
Получим общий интеграл:
.
Получим общий интеграл:
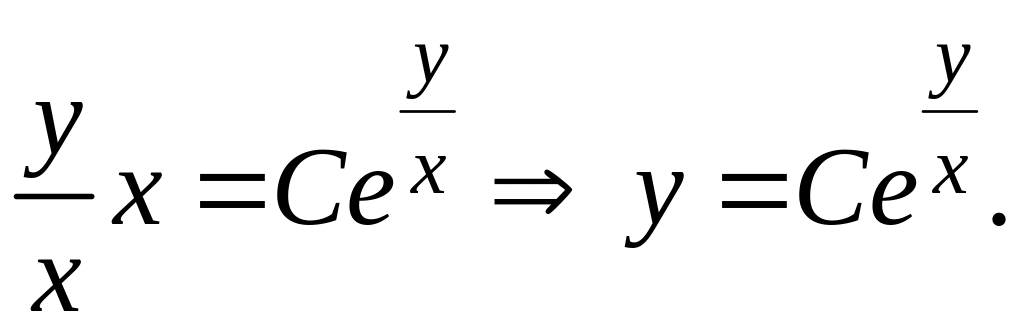
При
разделении переменных могли потерять
особые решения. Найдем их, если они
имеются. Для этого решим уравнение
![]() .
Непосредственно видно, что
не является решением Если
.
Непосредственно видно, что
не является решением Если
![]() ,
то
,
то
![]() .
С помощью подстановки можно убедиться,
что
– является решением данного ДУ.
.
С помощью подстановки можно убедиться,
что
– является решением данного ДУ.
Следовательно, к общему интегралу необходимо добавить решение .
Пример
2. Решить
уравнение
![]() .
.
Решение. Приведем данное уравнение к виду (3.3)
![]() .
.
Так
как функции
и
![]() – однородные первого порядка, то данное
уравнение – однородное. Сделаем замену
,
.
Тогда
– однородные первого порядка, то данное
уравнение – однородное. Сделаем замену
,
.
Тогда
![]() ,
,
предполагая,
что
![]() ,
сокращаем обе части равенства на
.
Далее имеем:
,
сокращаем обе части равенства на
.
Далее имеем:
![]() .
.
Разделяем переменные, интегрируем и находим общий интеграл ДУ:
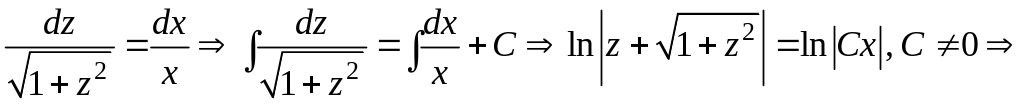
![]() .
.
После обратной замены получаем:
![]()
![]() .
.
Особое
решение только одно
,
так как
![]() .
.
Пример 3. Найти частное решение ДУ
![]() ,
,
удовлетворяющее
начальному условию
![]() .
.
Решение.
Легко видеть, что функция
![]() – однородная нулевого порядка. Сделаем
замену
,
.
Тогда
– однородная нулевого порядка. Сделаем
замену
,
.
Тогда
![]() .
.
Разделяем переменные
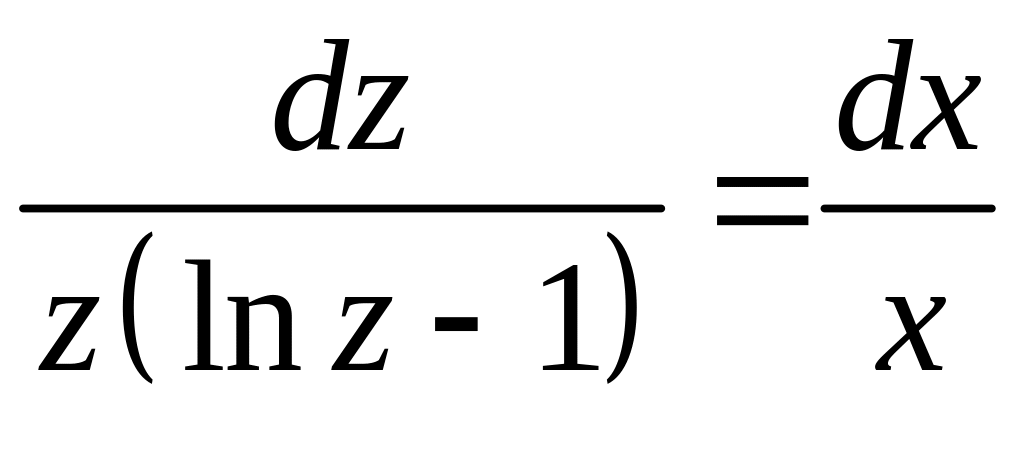 .
.
Интегрируем последнее равенство, получаем:
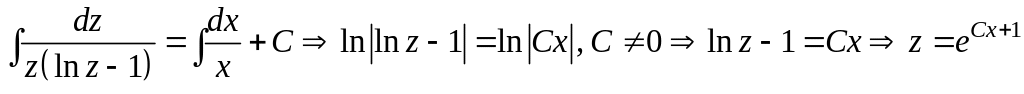 .
.
Подставляя вместо его значение, получим общее решение:
![]() .
.
Использовав начальное условие , определим значение С:
![]() .
.
Следовательно, частное решение исходного уравнения имеет вид:
![]() .
.
Пример 4. Найти общий интеграл ДУ
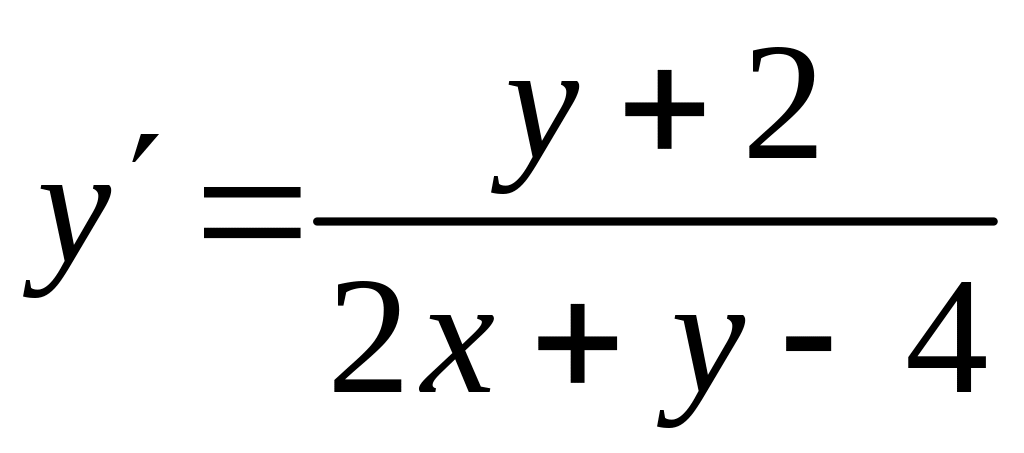 .
.
Решение. Положив , получаем:
![]()
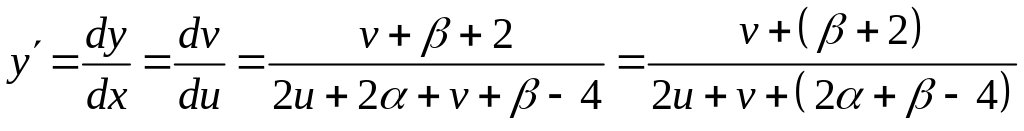 .
.
Подберем и так, чтобы уравнение стало однородным, т.е.
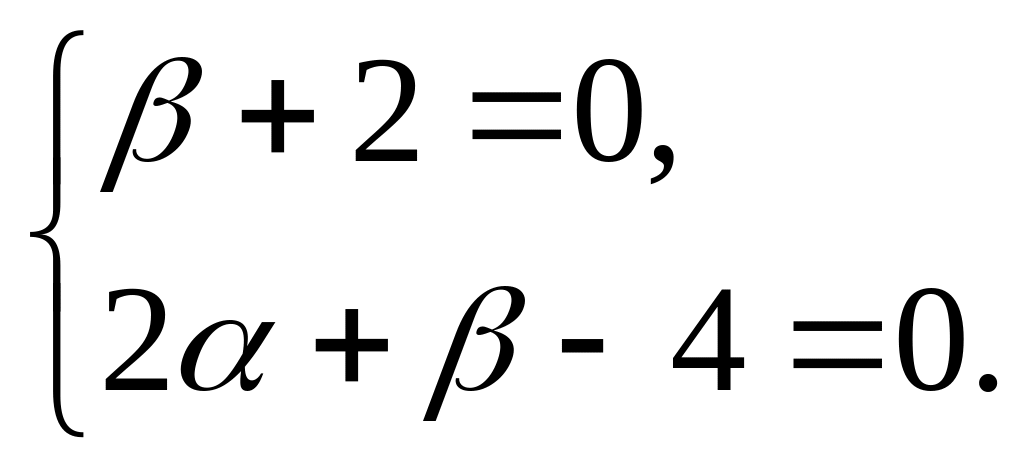
Находим,
что
![]() .
Заданное уравнение принимает вид:
.
Заданное уравнение принимает вид:
![]()
и будет являться однородным.
Решая
это однородное уравнение подстановкой
![]() ,
получаем уравнение:
,
получаем уравнение:
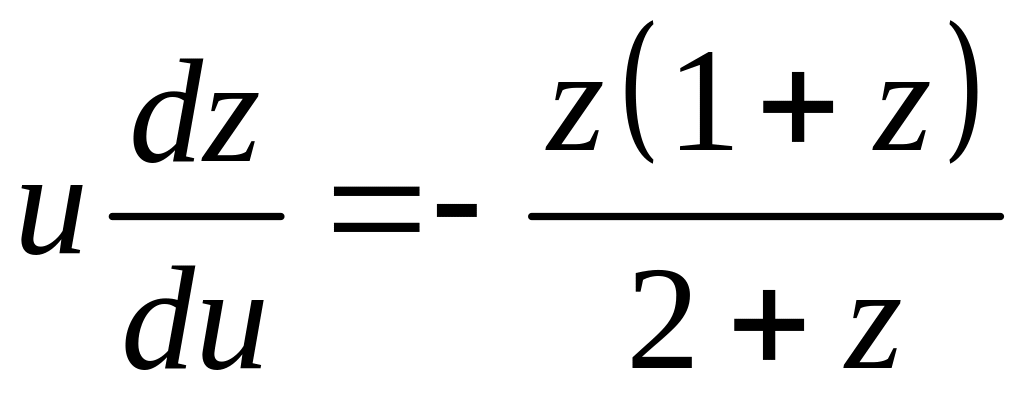
решением которого является:
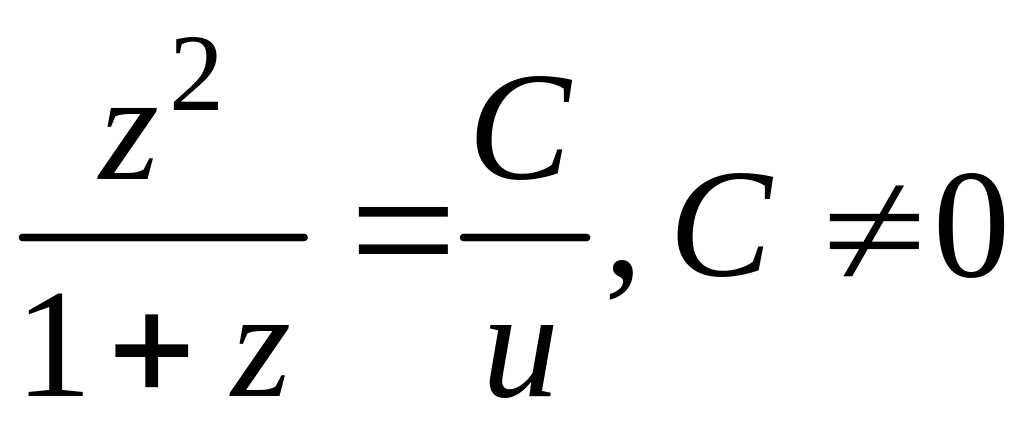 .
.
Подставляя
значение
![]() ,
получаем:
,
получаем:
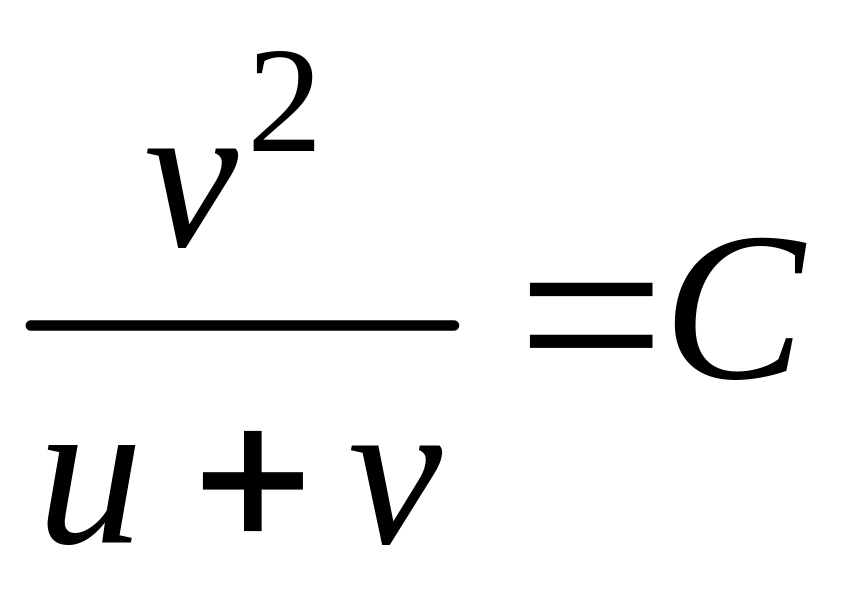 .
.
Так
как
![]() ,
т.е.
,
т.е.
![]() ,
имеем:
,
имеем:
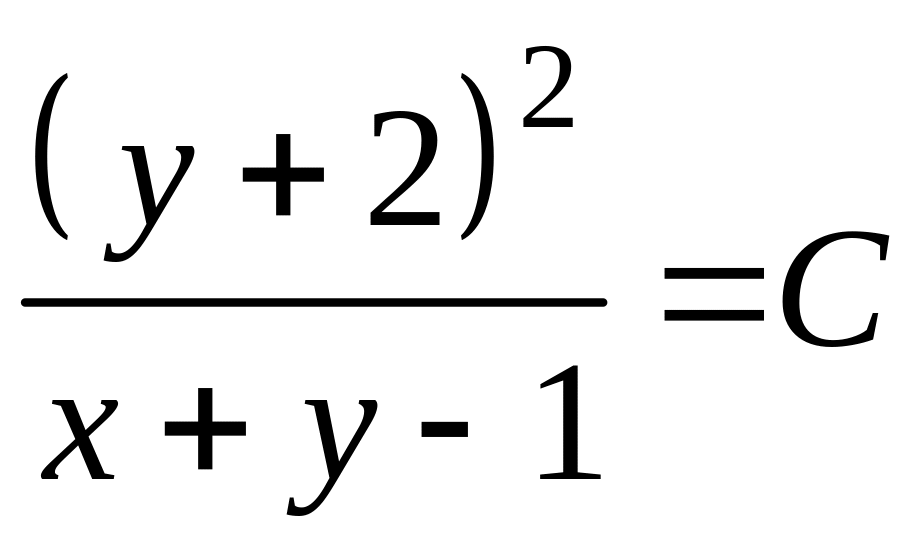 .
.


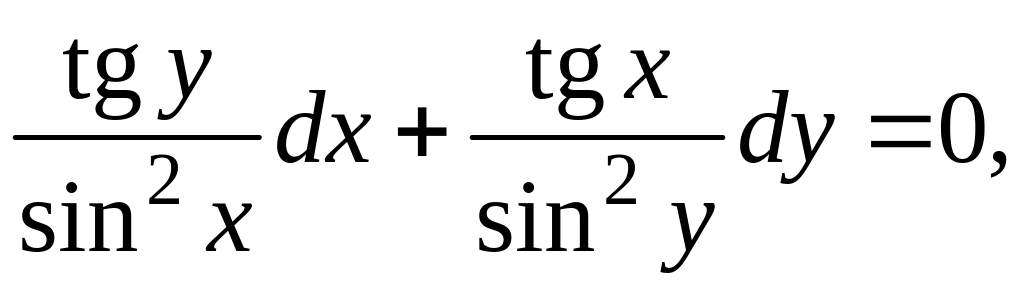
 ;
;