
- •9. Дифференциальные уравнения
- •9.1. Дифференциальные уравнения первого порядка Краткие теоретические сведения
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •9.2. Уравнения с разделяющимися переменными Краткие теоретические сведения
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •9.3. Однородные дифференциальные уравнения Краткие теоретические сведения
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •9.4. Линейные дифференциальные уравнения первого порядка. Уравнение я. Бернулли Краткие теоретические сведения
- •Метод и. Бернулли
- •Метод Лагранжа (метод вариации произвольной постоянной)
- •Уравнение я. Бернулли
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •Интегрирующий множитель
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •9.6. Дифференциальные уравнения второго и более высоких порядков, допускающие понижение порядка Краткие теоретические сведения
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •9.7. Линейные однородные уравнения с постоянными коэффициентами (лоду) Краткие теоретические сведения
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •9.8. Линейные неоднородные уравнения с постоянными коэффициентами второго и более высоких порядков (лнду) Краткие теоретические сведения
- •Метод вариации произвольных постоянных (метод Лагранжа)
- •Метод неопределенных коэффициентов
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •9.9. Приложение дифференциальных уравнений в экономике Краткие теоретические сведения
- •Примеры решения типовых задач
- •Задачи для самостоятельной работы
Задания для самостоятельной работы
n9.18. Найти общее решение ДУ:
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
ж)
|
з)
|
n9.19. Найти общее решение ДУ:
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
ж)
|
з)
|
n9.20. Найти общее решение ДУ:
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
ж)
|
з)
|
n9.21. Решить задачу Коши:
а)
|
б)
|
в)
|
г) |
д) |
е) |
ж)
|
з)
|
Ответы
9.7. Линейные однородные уравнения с постоянными коэффициентами (лоду) Краткие теоретические сведения
Линейным однородным уравнением n-го порядка с постоянными коэффициентами называется уравнение вида:
![]() ,
(7.1)
,
(7.1)
где
коэффициенты
![]() – некоторые действительные числа.
– некоторые действительные числа.
Дифференциальному уравнению (7.1) ставится в соответствие характеристическое уравнение, т.е. алгебраическое уравнение n-го порядка вида:
![]() .
(7.2)
.
(7.2)
Для
его составления достаточно в уравнении
(7.1) заменить
![]() .
.
Как
известно, уравнение (7.2) имеет n
корней. Обозначим их через
![]() .
.
Корни
уравнения (7.2) могут быть действительные
или комплексные, среди которых могут
быть и равные. Если уравнение имеет
равные корни, то в этом случае говорят,
что корень один и имеет кратность
![]() .
Так, например, уравнение
.
Так, например, уравнение
![]() имеет три равных корня:
имеет три равных корня:
![]() .
В этом случае корень
.
В этом случае корень
![]() имеет кратность
имеет кратность
![]() .
Если кратность корня равна единице, его
называют простым.
.
Если кратность корня равна единице, его
называют простым.
Общее решение дифференциального уравнения (7.1) строится в зависимости от характера корней уравнения (7.2):
1)
каждому действительному простому корню
![]() в общем решении соответствует слагаемое
вида
в общем решении соответствует слагаемое
вида
![]() ,
т.е. если все корни уравнения действительны
и различны
,
т.е. если все корни уравнения действительны
и различны
![]() ,
то общее решение уравнения (7.1) записывается
в виде:
,
то общее решение уравнения (7.1) записывается
в виде:
![]() ; (7.3)
; (7.3)
2) каждому действительному корню кратности в общем решении соответствует слагаемое вида:
![]() ;
(7.4)
;
(7.4)
3)
каждой паре комплексных сопряженных
простых корней
![]() в общем решении соответствует слагаемое
вида:
в общем решении соответствует слагаемое
вида:
![]() ;
(7.5)
;
(7.5)
4) каждой паре комплексных сопряженных корней кратности в общем решении соответствует слагаемое вида:
![]() .
.
Если
в уравнении (7.1)
![]() ,
то получаем линейное однородное
дифференциальное уравнение второго
порядка с постоянными
коэффициентами:
,
то получаем линейное однородное
дифференциальное уравнение второго
порядка с постоянными
коэффициентами:
![]() .
(7.6)
.
(7.6)
Характеристическое уравнение имеет вид:
![]() . (7.7)
. (7.7)
При его решении возможны три случая:
1*)
если
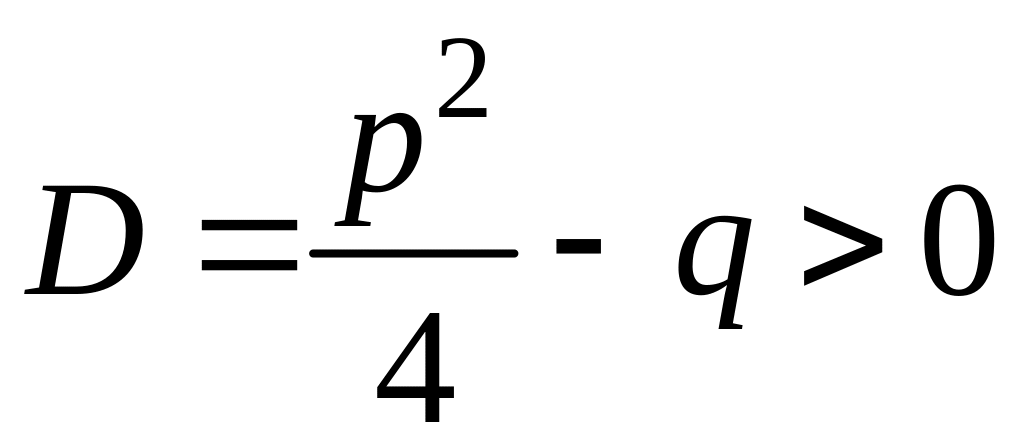 ,
то
,
то
![]() ,
и общее решение уравнения (7.6) имеет вид:
,
и общее решение уравнения (7.6) имеет вид:
![]() ;
;
2*)
если
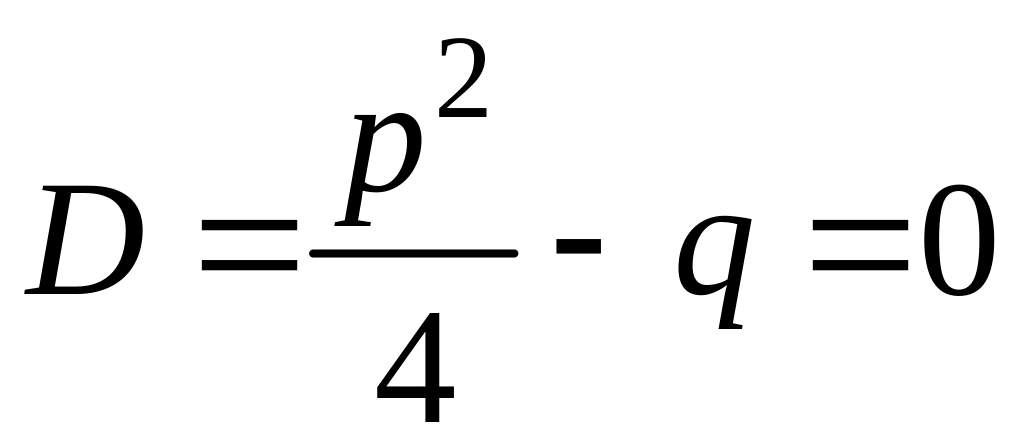 ,
то
,
то
![]() ,
т.е. уравнение (7.7) имеет один корень
кратности
,
т.е. уравнение (7.7) имеет один корень
кратности
![]() .
Тогда общее решение уравнения (7.6) имеет
вид:
.
Тогда общее решение уравнения (7.6) имеет
вид:
![]() ;
;
3*)
если
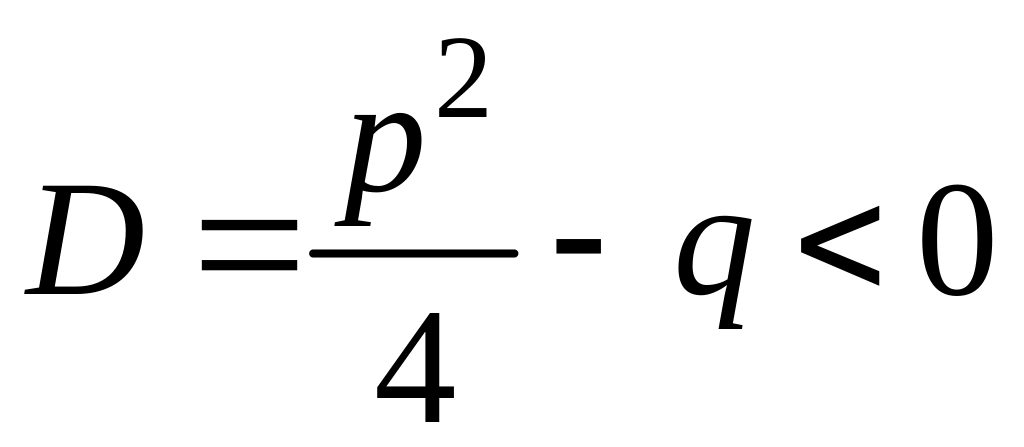 ,
то характеристическое уравнение имеет
комплексные корни
,
где
,
то характеристическое уравнение имеет
комплексные корни
,
где
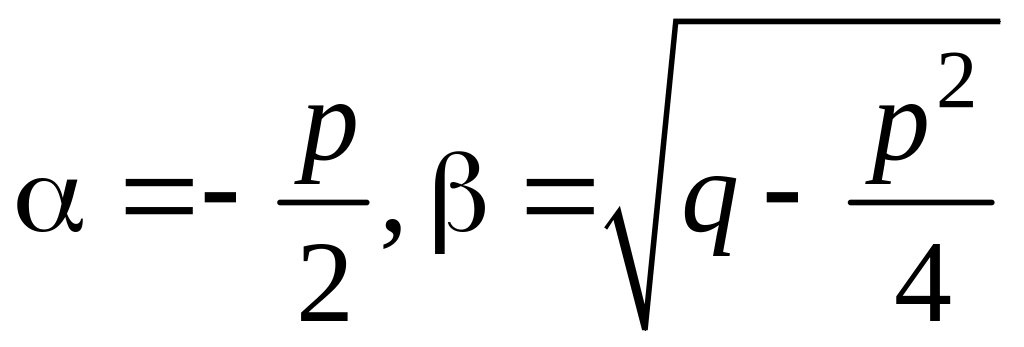 ,
и общее решение уравнения (7.6) имеет вид:
,
и общее решение уравнения (7.6) имеет вид:
![]() .
.
Примеры решения типовых задач
Пример 1. Найти общее решение для следующих однородных линейных дифференциальных уравнений второго порядка:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Решение.
а)
Характеристическое уравнение
![]() имеет различные корни:
имеет различные корни:
![]() ,
поэтому общее решение ДУ имеет вид:
,
поэтому общее решение ДУ имеет вид:
![]() .
.
б)
В данном случае характеристическое
уравнение
![]() имеет один корень кратности 2
имеет один корень кратности 2
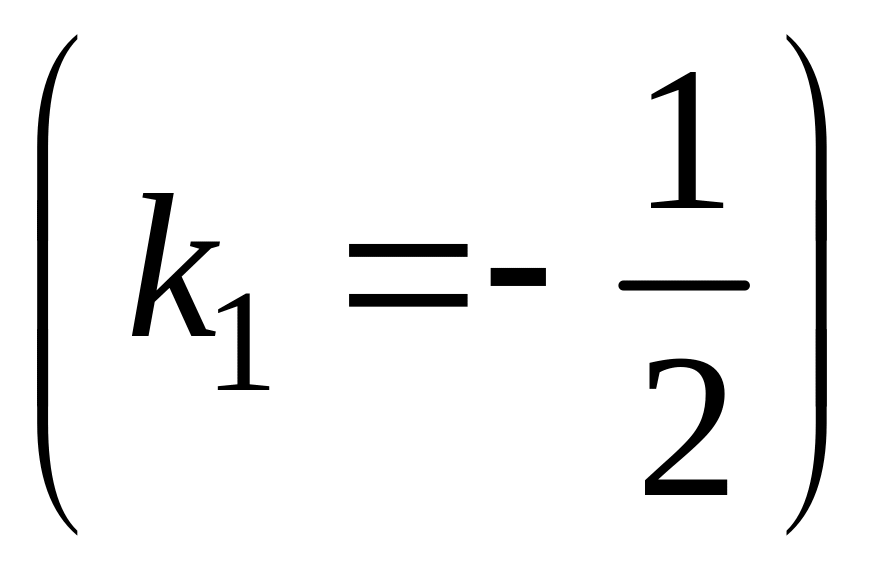 ,
следовательно, искомое общее решение
есть
,
следовательно, искомое общее решение
есть
![]() .
.
в)
Характеристическое уравнение имеет
комплексные корни
![]() ,
следовательно,
,
следовательно,
![]() .
Поэтому общее решение имеет вид:
.
Поэтому общее решение имеет вид:
![]() .
.
Пример 2. Найти общее решение для следующих однородных линейных дифференциальных уравнений высших порядков:
а)
![]() ;
б)
;
б)
![]() .
.
Решение.
а)
Составляем характеристическое уравнение
для данного ДУ и находим его корни:
![]() .
Получаем два корня кратности 2:
.
Получаем два корня кратности 2:
![]() .
.
На
основании формулы (7.4) общее решение
исходного уравнения имеет вид:![]() .
.
б) Характеристическое уравнение для данного ДУ имеет вид:
![]() .
.
Находим его корни:
![]()
![]() .
.
Получили
пять простых корней: три действительных
и два комплексно-сопряженных
![]() .
С учетом формул (7.3.) и (7.5.) общее решение
исходного ДУ имеет вид:
.
С учетом формул (7.3.) и (7.5.) общее решение
исходного ДУ имеет вид:
![]() .
.

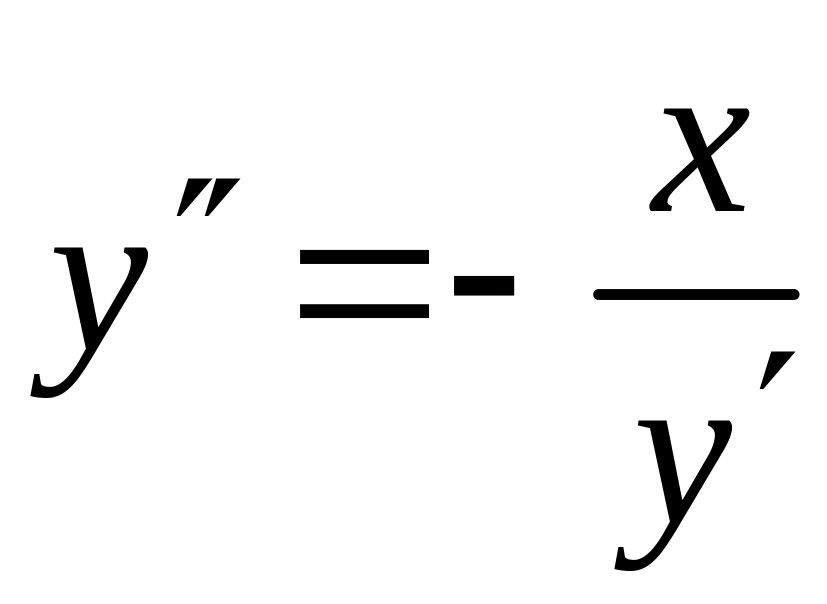 ;
;