
Часть I. Множества, соотвествия, отношения
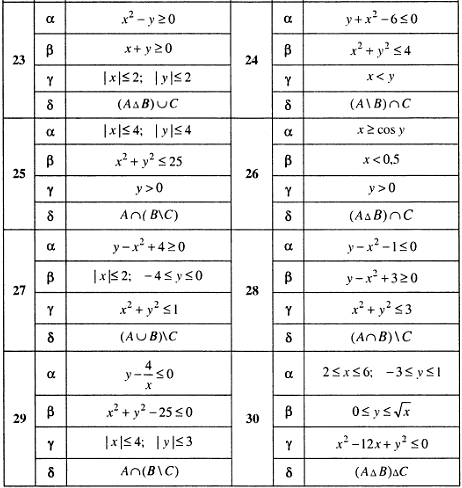
1. Операции над множествами
Запись
![]() означает, что элемент
означает, что элемент
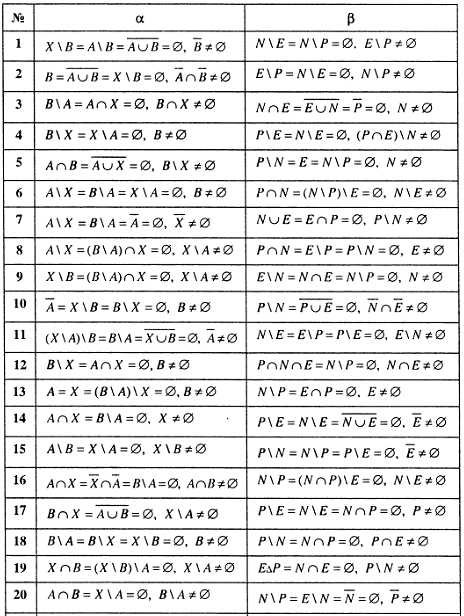
![]() принадлежит множеству
принадлежит множеству
![]() .
Если
не является элементом множества
,
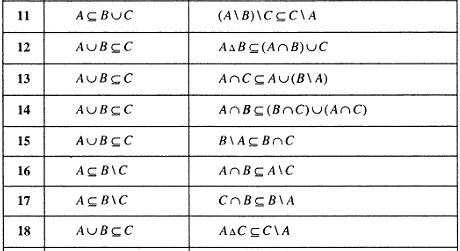
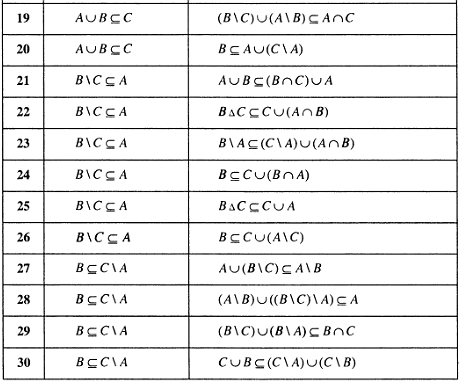
то пишут
.
Если
не является элементом множества
,
то пишут
![]() .
Два множества
и
.
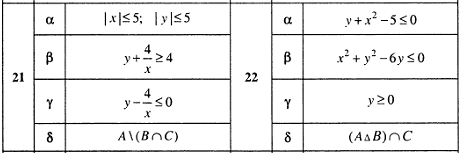
Два множества
и
![]() считаются равными, если они состоят
из одних и тех же элементов. Будем писать
считаются равными, если они состоят
из одних и тех же элементов. Будем писать
![]() ,
если
и
равны и
,
если
и
равны и
![]() в противном случае. Множество называется
пустым и обозначается
в противном случае. Множество называется
пустым и обозначается
![]() ,
если оно не содержит элементов.
,
если оно не содержит элементов.
Будем говорить, множество
включено во множество
,
и писать
![]() ,
если каждый элемент множества
является элементом множества
.
В этом случае
называется подмножеством множества
,
если каждый элемент множества
является элементом множества
.
В этом случае
называется подмножеством множества
![]() .
Считается, что для любого
справедливо включение
.
Считается, что для любого
справедливо включение
![]() .
.
Если
![]() и
,
то будем писать
и
,
то будем писать
![]() и говорить, что множество
строго включено во множество
или
множество
является собственным подмножеством
множества
.
и говорить, что множество
строго включено во множество
или
множество
является собственным подмножеством
множества
.
Семейство всех подмножеств данного
множества
обозначается
![]() .
.
Мощностью конечного множества
будем называть число его элементов.
Мощность множества (не
обязательно конечного)
обозначается
![]() .
.
Объединением множеств и называется множество
![]() .
.
Пересечением множеств и называется множество
![]()
Разностью множеств и называется множество
![]() .
.
Если все рассматриваемые множества
являются подмножествами некоторого
универсального множества
![]() ,
то разность
,
то разность
![]() называется дополнением
и обозначается
называется дополнением
и обозначается
![]() .
.
Симметрической разностью множества
и
называется множество
![]() .
.
Будем говорить, что множества
и
находятся в общем положении,
если существуют такие элементы
![]() ,
что
,
что
![]() и
и
![]() ,
,
![]() и
и
![]() ,
,
![]() и
и
![]() ,
иначе говоря, эти множества не являются
подмножествами друг друга и пересекаются.
,
иначе говоря, эти множества не являются
подмножествами друг друга и пересекаются.
Задание 1.1.
1. Справедливо ли в общем случае
утверждение: если
![]() и
и
![]() и
и
![]() ,
то
,
то
![]()
2. Может ли при некоторых
![]() и
и
![]() выполниться набор условий:
выполниться набор условий:
![]() и
и
и
и
и
и
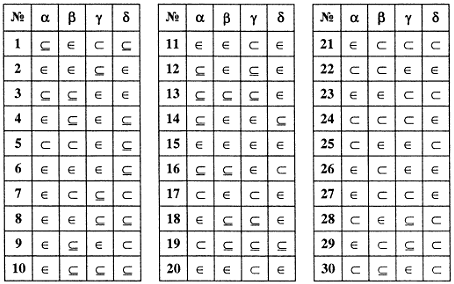
Примеры решения задания 1.1.
Пример 1.
а) Справедливо ли в общем случае
утверждение: если
![]() ,
,
![]() и
и
![]() ,
то
,
то
![]()
Решение. Пусть
![]() .
Так как
,
из определения включения следует, что
.
Так как
,
из определения включения следует, что
![]() .
Так как
и
.
Так как
и
![]() ,
то
,
то
![]() .
Так как
и
.
Так как
и
![]() ,
то
,
то
![]() .
Итак, из того, что произвольный элемент
.
Итак, из того, что произвольный элемент
![]() следует, что
следует, что
![]() .
На основании определения заключаем,
что
.
На основании определения заключаем,
что
![]() ,
то есть данное утверждение верно.
,
то есть данное утверждение верно.
б) Может ли при некоторых
![]() и
и
![]() выполняться набор условий:
выполняться набор условий:
![]() ,
и
,
и
?
,
и
,
и
?
Решение. Да, может. Это следует из
справедливости утверждения в пункте
а). Примером могут служить множества
![]() ,
,
![]() ,
,
![]() .
Тогда
.
Тогда
![]() ,
,
![]() ,
,
![]() и
и
![]() .
.
Пример 2.
а) Справедливо ли в общем случае
утверждение: если
,
![]() и
и
![]() ,
то
?
,
то
?
Решение. Пусть
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Тогда
и
.
Тогда
и
![]() .
.
Но в то же время неверно, что
![]() ,
так как единственный элемент
множества
не является элементом множества
,
состоящего из элементов
,
так как единственный элемент
множества
не является элементом множества
,
состоящего из элементов
![]() и
и
![]() .
Итак, утверждение из нашего примера 2а)
в общем случае неверно.
.
Итак, утверждение из нашего примера 2а)
в общем случае неверно.
б) Может ли при некоторых и выполняться набор условий: , , и ?
Решение. Да, может. Например,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Тогда
![]() ,
,
![]() ,
,
![]() и в то же время
и в то же время
![]() .
.
Задание 1.2. Для универсального
множества
![]() ,
множества
,
заданного списком, и для
,
множества
,
заданного списком, и для
![]() ,
являющегося множеством корней уравнения
,
являющегося множеством корней уравнения
![]()
1. Найти множества:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
2. Выяснить, какая из пяти возможностей
выполнена для множества
и
![]() :
:
![]() ,
или
,
или
![]() ,
или
,
или
![]() ,
или
,
или
![]() ,
или
и
,
или
и
![]() находятся в общем положении.
находятся в общем положении.
3. Найти
![]() и
и
![]() .
.
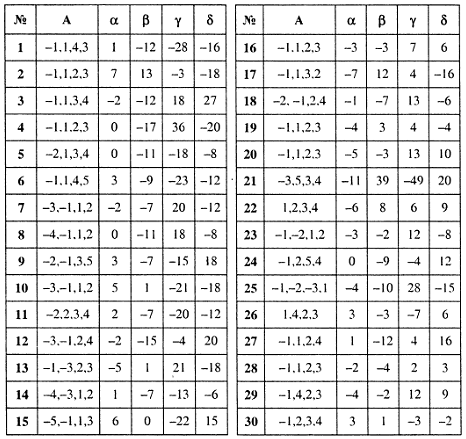
Пример решения задания 1.2.
Решим задание 1.2 для
![]() и уравнения
и уравнения
![]() .
.
Решение. Сначала найдём множество
корней данного уравнения. Подбором
устанавливаем, что корнем исходного
многочлена
![]() является
1; поделив этот многочлен на
является
1; поделив этот многочлен на
![]() ,
получим многочлен
,
получим многочлен
![]() .
Также подбором устанавливаем, что
.
Также подбором устанавливаем, что
![]() является корнем многочлена
является корнем многочлена
![]() и делим этот многочлен на
и делим этот многочлен на
![]() .
Получим многочлен
.
Получим многочлен
![]() .
Его корни совпадают и равны 4.
.
Его корни совпадают и равны 4.
Итак, множество
найдено,
![]() .
Теперь решаем пункты 1-3 данного задания.
.
Теперь решаем пункты 1-3 данного задания.
1.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
2. Так как
![]() и
и
![]() ,
,
![]() и
и
![]() ,
,
![]() ,
то множества
и
находятся в общем положении.
,
то множества
и
находятся в общем положении.
3.
![]() .
Видим, что
содержит 8 элементов, т.е.
.
Видим, что
содержит 8 элементов, т.е.
![]() .
.
Задание 1.3. Пусть
![]() и
– множество точек плоскости, координаты
которых удовлетворяют условиям
и
– множество точек плоскости, координаты
которых удовлетворяют условиям
![]() и
и
![]() соответственно. Изобразите в системе
координат
соответственно. Изобразите в системе
координат
![]() множество
,
полученное из множества
множество
,
полученное из множества
![]() и
по формуле
и
по формуле
![]() .
.
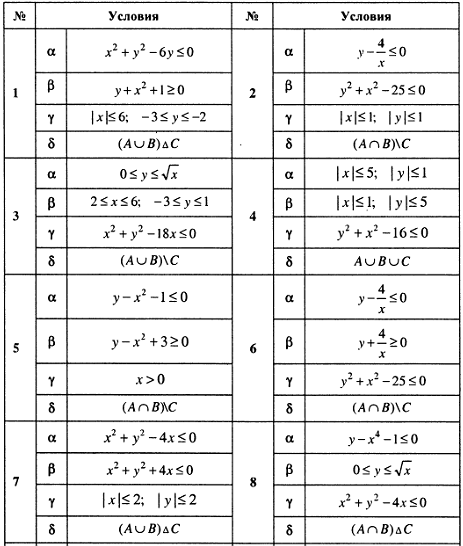

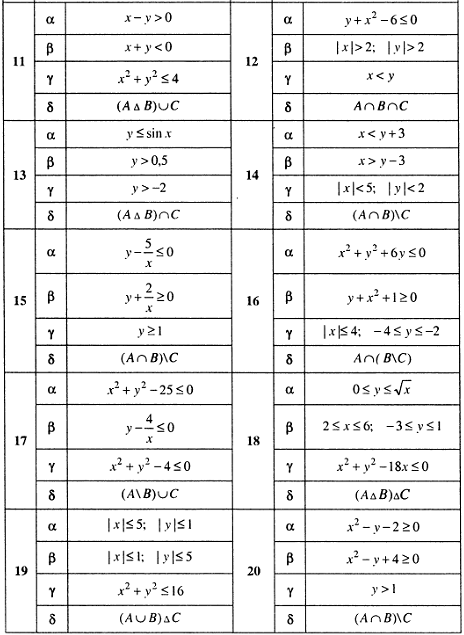
Пример решения задания 1.3.
Пусть
и
![]() множество
точек плоскости, координаты которых
удовлетворяют условиям
множество
точек плоскости, координаты которых
удовлетворяют условиям
![]() ,
,
![]() и
и
![]()
![]() соответственно. Изобразите в системе
координат
множество
,
полученное из множеств
и
по формуле
соответственно. Изобразите в системе
координат
множество
,
полученное из множеств
и
по формуле
![]() .
.
Решение. Множество
представляет из себя множество точек
круга радиуса 2 с центом в начале
координат, включающего границу,
![]() множество
точек плоскости, расположенных выше и
на прямой
множество
точек плоскости, расположенных выше и
на прямой
![]() ,
и
множество точек, лежащих внутри и на
границе квадрата
,
и
множество точек, лежащих внутри и на
границе квадрата
![]() ;
;
![]() .
.
Отметим горизонтальной штриховкой
множество
![]() ,
а вертикальной – множество
(рис.1, а)
,
а вертикальной – множество
(рис.1, а)
Удалив из области, помеченной вертикальной штриховкой, точки области, помеченной горизонтальной штриховкой, мы получим множество точек, образующих . Изобразим результат, отметив точки множества вертикальной штриховкой (рис. 1, б).

Рис. 1
Задание 1.4.
1. Существуют ли множества
![]() такие, что выполняется набор условий
такие, что выполняется набор условий
![]() ?
?
2. Существуют ли множества
![]() такие, что выполняется набор условий
такие, что выполняется набор условий
![]() ?
?


Пример решения задания 1.4.
1. Существуют ли множества
такие, что выполняется набор условий:
![]() ,
,
![]() ,
,
![]() ?
?
Решение. Изобразим множества
в виде прямоугольников, расположенных
на плоскости в общем положении, и
поставим в каждой области, на которые
плоскость разбита прямоугольниками,
по одному символу: символ 4, например,
обозначает список всех элементов,
попавших во множества
и
,
но не попавших в
|
5
8
Рис. 2 |
Изменим множества так, чтобы выполнились условия нашего задания.
Из того, что
,
следует, что множество
![]() не должно содержать элементов, т.е. из
удаляем 8 и 3. Чтобы выполнилось условие
,
нужно удалить элементы списков 1, 4, 7.
Тогда получится, что множества
и
имеют следующий вид:
не должно содержать элементов, т.е. из
удаляем 8 и 3. Чтобы выполнилось условие
,
нужно удалить элементы списков 1, 4, 7.
Тогда получится, что множества
и
имеют следующий вид:
![]() ,
,
![]() ,
,
![]() .
Заметим, что для этих множеств
.
Заметим, что для этих множеств
![]() .
.
Если под символами 2, 5 и 6 будем понимать соответствующие числа, то мы получим конкретный пример множества , для которых выполнены все условия заданного набора требований.
2. Существуют ли множества
такие, что выполняется набор условий:
![]() ,
,
![]() ?
?
Решение. Попробуем построить
множества
так же, как мы это делали в п. 1. Пусть
![]() ,
,
![]() ,
,
![]() .
Чтобы выполнялось условие
.
Чтобы выполнялось условие
![]() ,
удаляем элементы списков 6, 7. Для
выполнения условия
,
удаляем элементы списков 6, 7. Для
выполнения условия
![]() удаляем
элементы из списков 2, 3. Но тогда множество
удаляем
элементы из списков 2, 3. Но тогда множество
![]() не будет содержать элементов. Итак, мы
показали, что этот набор условий
противоречив, т.е. не существует множеств
таких, что выполнены условия упражнения.
не будет содержать элементов. Итак, мы
показали, что этот набор условий
противоречив, т.е. не существует множеств
таких, что выполнены условия упражнения.
Задание 1.5. Выяснить взаимное
расположение множеств
![]() ,
если
– произвольные подмножества универсального
множества
.
,
если
– произвольные подмножества универсального
множества
.

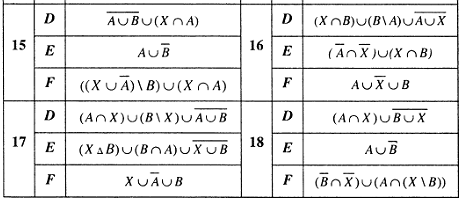
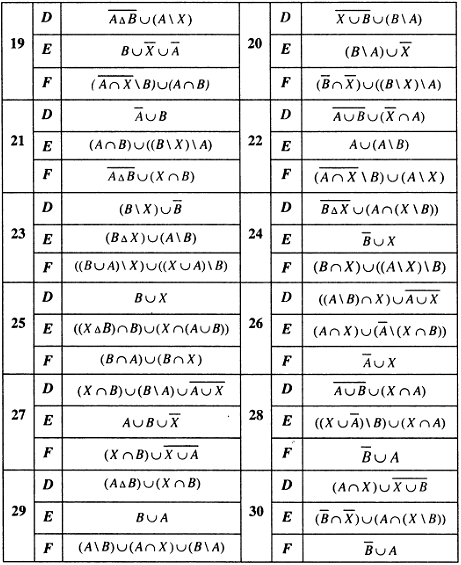
Пример решения задания 1.5.
Выяснить взаимное расположение множеств:
![]() ,
,
![]() ,
,
![]() ,
если
–
произвольные подмножества универсального
множества
.
,
если
–
произвольные подмножества универсального
множества
.
Решение. Возьмём множества
,
находящиеся в общем положении:
,
,
.
В нашем случае, как и при решении задания
1.3, цифры обозначают соответствующие
списки переменных. Тогда
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
т.е.
,
т.е.
![]() ,
,
![]() ,
,
![]() .
.
Итак, видим, что включения
![]() и
и
![]() выполняются для произвольных множеств
.
выполняются для произвольных множеств
.
Если символы 1, 2, 4, 5, 6, 7 обозначают
соответствующие числа, имеем, что
![]() и
и
![]() ,
,
![]() и
и
![]() ,
,
![]() ,
т.е. множества
и
,
т.е. множества
и
![]() могут находиться в общем положении.
могут находиться в общем положении.
Задание 1.6. Проверить, что для любых
множеств
![]() выполнение включения
влечёт выполнение включения
.
выполнение включения
влечёт выполнение включения
.

Пример решения задания 1.6.
Доказать, что для любых множеств
выполнение включения
![]() влечёт
выполнение включения
влечёт
выполнение включения
![]() .
.
Решение. Возьмем множества
находящиеся в общем положении:
,
,
![]() .
В нашем случае, как и при решении
предыдущих заданий, цифры обозначают
соответствующие списки переменных.
.
В нашем случае, как и при решении
предыдущих заданий, цифры обозначают
соответствующие списки переменных.
Тогда
![]() из включения
следует, что список 1 пуст,
из включения
следует, что список 1 пуст,
![]() .
Рассмотрим
.
Рассмотрим
![]() и
и
![]() .
Так как
.
Так как
![]() ,
то включение
доказано в предположении, что выполнено
включение
.
,
то включение
доказано в предположении, что выполнено
включение
.
Задание 1.7. Для произвольных множеств
![]() проверить, является ли выполнение
включения
необходимым и достаточным условием
выполнения равенства
.
проверить, является ли выполнение
включения
необходимым и достаточным условием
выполнения равенства
.


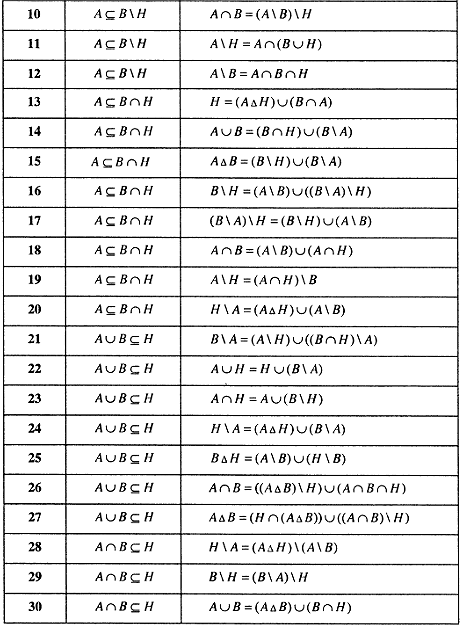
Пример решения задания 1.7.
Для произвольных множеств
![]() проверить, является ли выполнение
включения
проверить, является ли выполнение
включения
![]() необходимым и достаточным условием
выполнения равенства
необходимым и достаточным условием
выполнения равенства
![]() .
.
Решение. Рассмотрим множества
:
,
,
![]() .
В нашем случае, как и при решении
предыдущих заданий, цифры обозначают
соответствующие списки переменных.
.
В нашем случае, как и при решении
предыдущих заданий, цифры обозначают
соответствующие списки переменных.
1. Посмотрим, какие множества мы получим,
если потребуем выполнения условия
.
и, чтобы было выполнено включение
,
списки 1, 4, 6 должны быть пусты, и множества
будут таковы:
![]() ,
,
![]() ,
.
Тогда
,
.
Тогда
![]() ,
выполнено.
,
выполнено.
2. Посмотрим, какой вид примут множества
![]() ,
,
![]() ,
,
чтобы выполнялось равенство
.
,
,
чтобы выполнялось равенство
.
![]() .
.
Для выполнения равенства
нужно, чтобы списки 1, 4 и 6 были пусты, и
мы приходим к тем же множествам, что и
в п.1, т.е.
![]() ,
,
![]() ,
.
,
.
Видим, что в этом случае
![]()
Значит, доказано, что для любых множеств выполнение включения является необходимым и достаточным условием выполнения равенства .
Задание 1.8. Решить систему соотношений относительно множества и указать условия совместимости системы.
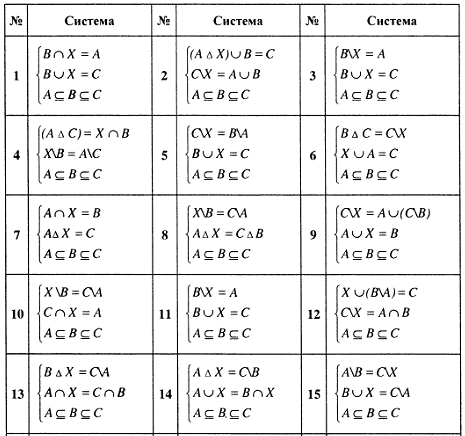
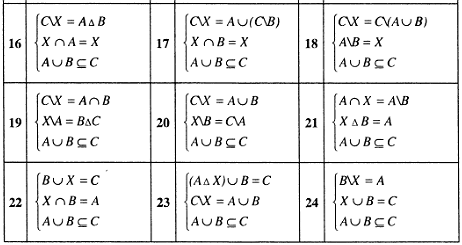

Пример решения задания 1.8.
Решить задание 1.8 для системы
Решение.
I. Построим множества
общего положения
|
Рис. 3 |
Символом 1 обозначим список элементов
множества
,
не попавших ни в одно из множеств
,![]() символом 7 – список элементов, попавших
в каждое из множеств
символом 7 – список элементов, попавших
в каждое из множеств
![]() и т.д. Будем иметь:
и т.д. Будем иметь:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
1.
![]() ,
,
![]() .
Эти множества равны в силу первого
уравнения системы, значит, списки
элементов 2, 4, 5, 7 и 8 пусты. Получили:
.
Эти множества равны в силу первого
уравнения системы, значит, списки
элементов 2, 4, 5, 7 и 8 пусты. Получили:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
2.
![]() ,
,
![]() .
Данные множества равны в силу второго
уравнения системы, следовательно, списки
элементов 3 и 9 пусты, и наши множества
примут вид:
.
Данные множества равны в силу второго
уравнения системы, следовательно, списки
элементов 3 и 9 пусты, и наши множества
примут вид:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Видим, что
![]() ,
,
![]() ,
,
![]() .
.
II. Проверим, что множество
![]() является решением исходной системы.
является решением исходной системы.
Если
и
![]() ,
то
и можно записать:
,
то
и можно записать:
![]() ,
,
![]() ,
где
,
где
![]() – списки элементов.
– списки элементов.
Пусть
![]() ,
тогда:
,
тогда:
![]() ,
,
![]() ,
,
![]() .
.
Видим, что все соотношения системы удовлетворяются, т.е. множество является решением исходной системы при выполнении условий , .
Ответ: , , .
Задание 1.9. Решить систему уравнений относительно множества и указать условия совместности системы или доказать её несовместность.
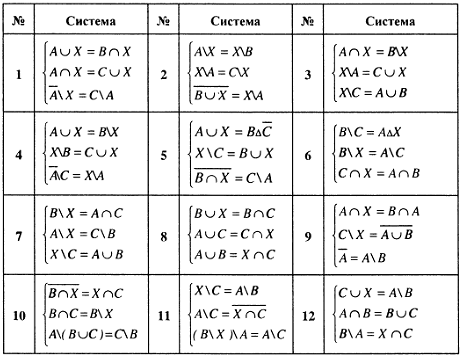
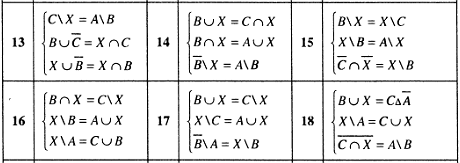
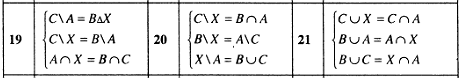
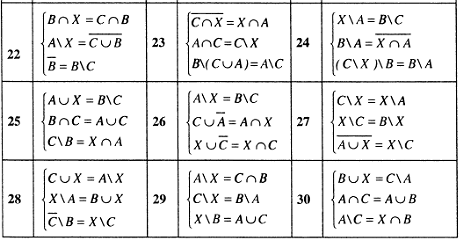
Пример решения задания 1.9.
Решить задание 1.9 для системы
![]()
Решение. Построим множества общего
положения
![]() ,
являющиеся подмножествами универсального
множества
.
Для этого выпишем все 16 различных
двоичных наборов размерности 4. Пусть
разряды этих наборов слева направо
соответствуют множествам
(табл. 1). Символом 1 обозначим список
элементов универсального множества
,
не попавших ни в одно из множеств
,
являющиеся подмножествами универсального
множества
.
Для этого выпишем все 16 различных
двоичных наборов размерности 4. Пусть
разряды этих наборов слева направо
соответствуют множествам
(табл. 1). Символом 1 обозначим список
элементов универсального множества
,
не попавших ни в одно из множеств
![]() (соответствующая
строка состоит из нулей), а символом 4 –
список элементов, не попавших ни в
,
ни в
,
но попавших в
и
(в
четвёртой строке нули относятся к
столбцам А и В, единицы к столбцам
С и Х ) и т.д.
(соответствующая
строка состоит из нулей), а символом 4 –
список элементов, не попавших ни в
,
ни в
,
но попавших в
и
(в
четвёртой строке нули относятся к
столбцам А и В, единицы к столбцам
С и Х ) и т.д.
Таблица 1
№ |
|
|
|
|
№ |
|
|
|
|
1 |
0 |
0 |
0 |
0 |
9 |
1 |
0 |
0 |
0 |
2 |
0 |
0 |
0 |
1 |
10 |
1 |
0 |
0 |
1 |
3 |
0 |
0 |
1 |
0 |
11 |
1 |
0 |
1 |
0 |
4 |
0 |
0 |
1 |
1 |
12 |
1 |
0 |
1 |
1 |
5 |
0 |
1 |
0 |
0 |
13 |
1 |
1 |
0 |
0 |
6 |
0 |
1 |
0 |
1 |
14 |
1 |
1 |
0 |
1 |
7 |
0 |
1 |
1 |
0 |
15 |
1 |
1 |
1 |
0 |
8 |
0 |
1 |
1 |
1 |
16 |
1 |
1 |
1 |
1 |
Имеем следующие списки:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
1.
![]() ,
,
![]() .
Эти множества равны в силу первого
уравнения системы, значит, списки
элементов 2, 4, 5, 8, 9, 11, 14 и 15 пусты. Получили:
.
Эти множества равны в силу первого
уравнения системы, значит, списки
элементов 2, 4, 5, 8, 9, 11, 14 и 15 пусты. Получили:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
2.
![]() ,
,
![]() .
Данные множества равны в силу второго
уравнения системы, следовательно, списки
элементов 6, 10, 13 пусты и наши множества
примут вид
.
Данные множества равны в силу второго
уравнения системы, следовательно, списки
элементов 6, 10, 13 пусты и наши множества
примут вид
![]() ,
,
![]() ,
,
![]() ,
.
,
.
3.
![]() ,
,
![]() ,
в силу третьего уравнения системы
получаем, что список 7 пуст, и
,
в силу третьего уравнения системы
получаем, что список 7 пуст, и
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Видим, что
![]() ,
,
![]()
II. Проверим, что множество является решением исходной системы.
Если выполнены включения
,
то можно записать:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
где
,
где
![]() списки элементов.
списки элементов.
Пусть
![]() ,
тогда
,
тогда
![]() ,
,
![]() ,
,
![]() .
.
Видим, что все уравнения системы
удовлетворяются, т.е. множество
![]() является решением исходной системы при
выполнении включений
.
является решением исходной системы при
выполнении включений
.
Ответ: , .
Задание 1.10. Для произвольных множеств
![]() проверить равносильность систем
и
.
проверить равносильность систем
и
.


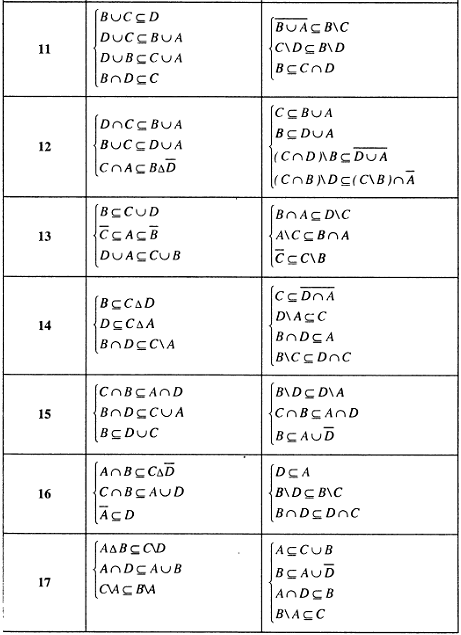
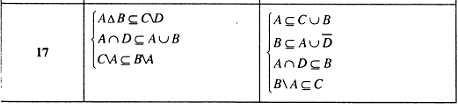
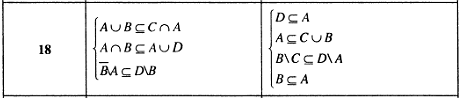
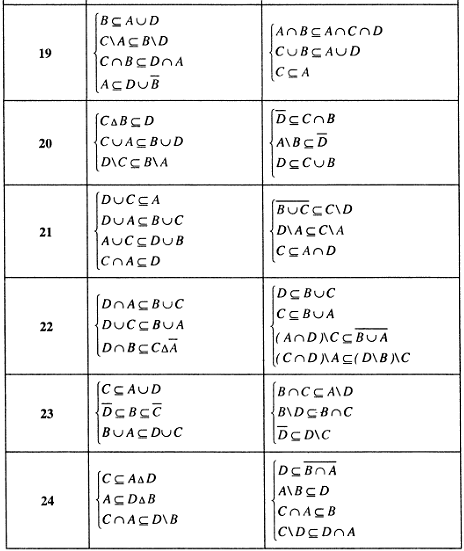
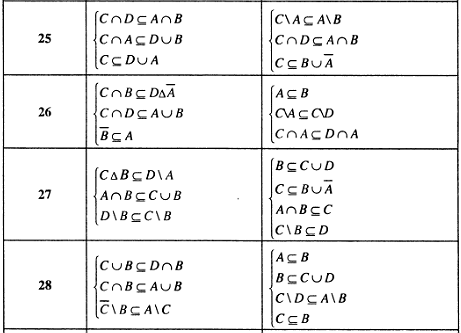

Пример решения задания 1.10.
Проверить равносильность систем
![]() и
и
![]() .
.
Решение. Возьмём множества общего
положения
![]() ,
являющиеся подмножествами универсального
множества
.
Пользуясь техникой, описанной в решении
примера 1.9 будем иметь:
,
являющиеся подмножествами универсального
множества
.
Пользуясь техникой, описанной в решении
примера 1.9 будем иметь:
,
![]() ,
,
![]() ,
,
,
![]() .
.
1. Рассмотрим включения, вошедшие в систему (*).
![]() ,
,
![]() .
.
По условию,
![]() ,
следовательно, список 6, 8, 14 пуст. Значит,
,
следовательно, список 6, 8, 14 пуст. Значит,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Для второго включения имеем:
![]() ,
,
![]() .
.
Так как
![]() ,
то
,
то
![]() .
Множества
и
можно записать так:
.
Множества
и
можно записать так:
![]() ,
,
![]() .
.
И, наконец,
![]() ,
то есть
,
то есть
![]() .
Откуда следует, что
.
Откуда следует, что
![]() .
.
Итак, множества
![]() и
таковы:
и
таковы:
,
![]() ,
,
![]() ,
,
![]() .
.
Проверим, при полученных и , выполнение включений (**):
![]() ,
поэтому включение
,
поэтому включение
![]() выполняется независимо от вида множества
выполняется независимо от вида множества
![]() .
.
![]() ,
,
![]() ,
значит,
,
значит,
![]() и второе включение также выполнено.
и второе включение также выполнено.
Наконец,
![]() ,
,
![]() и
и
![]() .
.
Получили, что все множества и удовлетворяющие системе включений (*), удовлетворяют также системе (**).
2. Пусть теперь выполняется система (**).
Так же, как и в первой части доказательства, возьмём множества
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Получим
![]() ,
,
![]() ,
,
и из выполнения включения
следует, что
![]() .
.
Рассматриваемые множества примут вид:
![]() ,
,
,
![]() ,
,
![]() ,
,
![]() .
.
Тогда
![]() ,
,
![]() .
.
Из включения
следует, что
![]() ,
значит,
,
значит,
![]() ,
,
![]() ,
,
![]() ,
,
,
![]() .
.
Следовательно,
![]() ,
,
![]() ,
,
Из включения
следует, что
![]() ,
значит,
,
значит,
![]() ,
,
![]() ,
,
![]() ,
,
,
![]() .
.
Проверим для этих множеств выполнение включений системы (*):
![]() ,
,
![]() и включение
выполнено.
и включение
выполнено.
![]() ,
,
![]() ,
включение
,
включение
![]() выполнено.
выполнено.
И, наконец,
![]() и
также верно. Итак, доказано, что системы
(*) и (**) равносильны.
и
также верно. Итак, доказано, что системы
(*) и (**) равносильны.








