Плохотников К.Э., Николенко В.Н. Теория вероятностей и математическая статистика в пакетах MATLAB и STATISTICA

Семинар №3 Элементы Комбинаторики

Решены несколько задач, иллюстрирующих процедуру подсчета простейших комбинаторных конфигураций: размещений, перестановок, сочетаний. Определяется биномиальное распределение, и решаются некоторые задачи.

§1. Размещения, перестановки и сочетания

Размещением из n элементов по m называется любое упорядоченное подмножество из m элементов множества, состоящего из n различных элементов.

Число размещений в общем случае определяется по формуле:

. (1)

Задача №1. Построить все размещения из трех букв русского алфавита.

Вначале подсчитаем число возможных размещений по формуле (1), тогда найдем

.

Для построения всех 32 736 размещений воспользуемся программой MATLAB, которая приведена на листинге №1.

%Листинг №1

clear all

%Загружаем русский алфавит в массив

x=['а','б','в','г','д','е','ё','ж','з','и',...

'й','к','л','м','н','о','п','р','с','т',...

'у','ф','х','ц','ч','ш','щ','ъ','ы','ь',...

'э','ю','я'];

%Определяем переменную, которая подсчитает количество

%размещений трех букв из 33

A_3_33=0;

%Выводим все комбинации трех букв из 33

for i=1:33

for j=1:33

for k=1:33

if (i~=j)&&(i~=k)&&(j~=k)

A_3_33=A_3_33+1;

disp([x(i),x(j),x(k)])

end

end

end

end

%Выводим общее количество размещений трех букв из 33

A_3_33

После запуска программы листинга №1 получим список всех возможных трехбуквенных слов и число таких слов. Фрагмент списка размещений и их общее число приведены на рис.1.

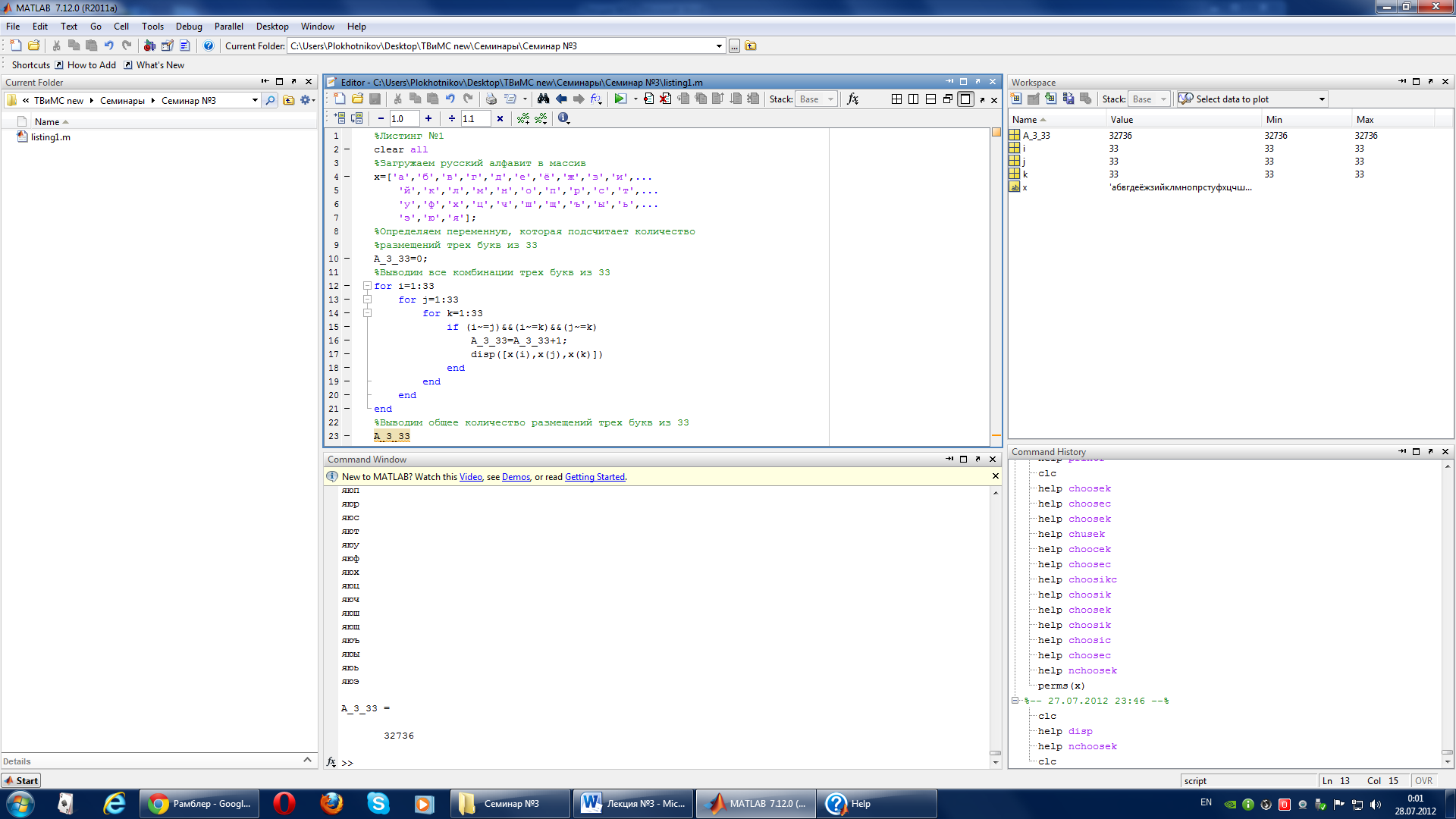
Рис.1. Фрагмент списка размещений и их общее число

Задача №2. Подсчитать количество размещений ста файлов по 1000 папкам.

Формально данная задача ничем не отличается от предыдущей, т.к. здесь также для подсчета размещений необходимо использовать формулу (1). Формальное использование формулы (1) приводит к следующему выражению:

. (2)

Проблема состоит в том, что полученное число слишком большое или, иначе, комбинаторно огромное. Для подсчета числа (2) необходимы специальные средства, которые, в частности, предоставляет MATLAB. На листинге №2 приведена программа, которая подсчитывает число (2), а также количество цифр, которое описывает данное число.

%Листинг №2

clear all

%Определяем символическую переменную, в которую

%загрузим число размещений 100 файлов по 1000 папкам

x=sym('1');

%Активируем цикл перемножений

for i=1000:-1:901

x=x*i;

end

%Выводим число размещений 100 файлов по 1000 папкам

x

%Выводим длину числа размещений 100 файлов по 1000 папкам

length(char(x))

После запуска программы листинга №2 найдем искомое число (2), оно равно:

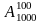= 59589266322404781554893890579461…,

причем выписано лишь начало числа. Все число включает 298 цифр.

Отметим, что размещения согласно формуле (1) в пакете MATLAB могут быть подсчитаны при не слишком большом значении n с помощью функции произведения prod(n:–1:n – m + 1).

Перестановки из n элементов называется любое упорядоченное множество, в которое входят по одному сразу все n различных элементов данного множества.

Количество перестановок n объектов принято обозначать символом P_n, при этом

P_n = n!, (3)

где n! = 12…n (читается “n – факториал”).

Отметим, что с учетом определения факториала формулу (1) для размещений можно переписать в виде:

.

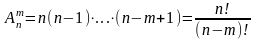Задача №3. На вернисаже предполагается разместить 1000 произведений искусства. Сколькими способами эти произведения искусств можно разместить.

Искомое количество размещений сводится к перестановкам, которое подсчитывается согласно формуле (3), т.е.

P₁₀₀₀ = 12…1000. (4)

Расчет по формуле (4) сталкивается с проблемой того, что это число P₁₀₀₀ слишком большое. Данная ситуация аналогично той, которая возникла при подсчете числа размещений в (2).

Для подсчета числа (4) поступим аналогично примеру №3, т.е. составим программу в среде MATLAB. Искомая программа приведена на листинге №3.

%Листинг №3

clear all

%Определяем символическую переменную, в которую

%загрузим число перестановок 1000 произведений искусства

x=sym('1');

%Активируем цикл перемножений

for i=1:1000

x=x*i;

end

%Выводим число перестановок 1000 произведений искусства

x

%Выводим длину числа перестановок 1000 произведений искусства

length(char(x))

После того, как программа листинга №3 отработает, будет найдено число 1000! и количество цифр, которые входят в данное число.

Получится в итоге:

P₁₀₀₀ = 402387260077093773543702433923003985719…,

причем выписано лишь начало числа. Все число включает 2568 цифр.

Отметим, что при построении формулы числа перестановок (3) считалось, что все n объектов различны. Если это не так, т.е. среди n объектов есть совпадающие, например, n₁ совпадающих объектов, n₂ совпадающих объектов и т.д., причем n₁ + n₂ + … = n. В этом случае количество перестановок подсчитывается по другой формуле, а именно,

. (3)

где n₁ + n₂ + … = n.

В пакете MATLAB можно подсчитать число перестановок P_n = n!, если воспользоваться функцией factorial(n), которая определена при не слишком большом параметре n (n < 22).

Задача №4. Найти все перестановки набора {A,B,B,C,C,C}.

В заданном наборе символов буква A повторяется один раз, буква B повторяется два раза, буква C — три раза. Это означает, что для оценки числа искомого набора перестановок необходимо воспользоваться формулой (3). В этом случае имеем

.

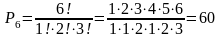Теперь осталось найти все эти перестановки. На листинге №4 приведена программа, которая подсчитывает и выводит искомые перестановки.

%Листинг №4

clear all

%Определяем исходный набор символов

a=['A','B','B','C','C','C'];

%Определяем матрицу, в которую будут загружены

%искомые перестановки

A(1,:)=a;

%Определяем матрицу всех перестановок набора {1,2,3,4,5,6}

P=perms(1:6);

%Определяем число перестановок, которое равно 6!

L=length(P(:,1));

%Определяем переменную, которая фиксирует номер

%искомой перестановки

i=1;

%Включаем цикл перебора всех 6! перестановок,

%отбрасывая среди них те которые совпадают с предыдущими

for l=1:L

%Определяем текущую перестановку

b=[a(P(l,1)),a(P(l,2)),a(P(l,3)),a(P(l,4)),a(P(l,5)),a(P(l,6))];

%Определяем отличается ли она от предыдущих

f=true;

for j=1:i

f=f*(sum(b==A(j,:))~=6);

end

%Если текущая перестановка отличается от предыдущих,

%то загружаем ее в массив А

if f

i=i+1;

A(i,:)=b;

end

end

%Выводим массив искомых перестановок

A

%Выводим число искомых перестановок

length(A(:,1))

После того, как программа отработает, получится картина, похожая на ту, которая приведена на рис.2.

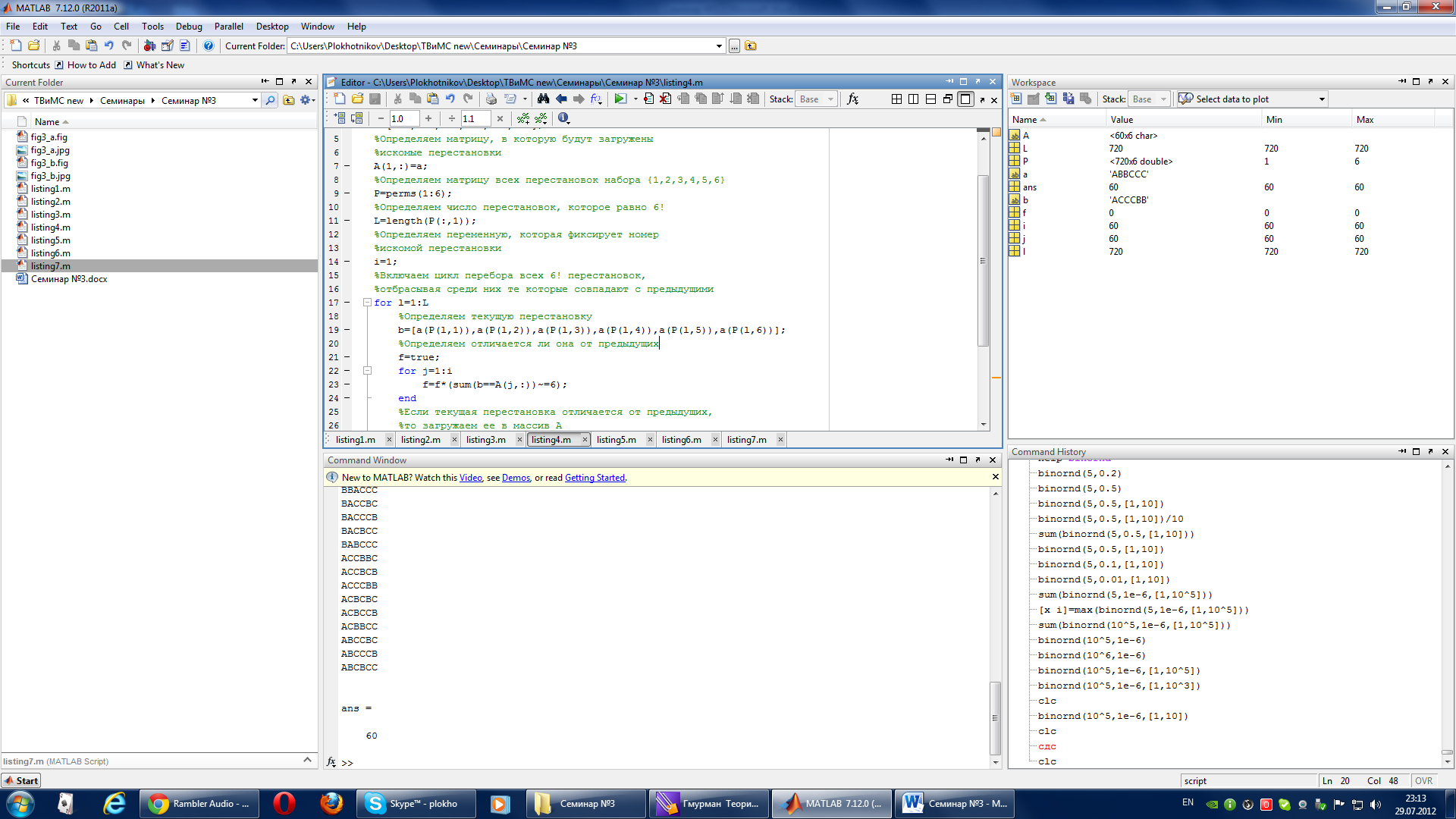
Рис.2. Все перестановки набора {A,B,B,C,C,C} и число таких перестановок

Более компактно все 60 перестановок набора {A,B,B,C,C,C} приведены в виде таблицы №1.

Таблица №1. Все 60 перестановок набора символов {A,B,B,C,C,C}
ABBCCC	CCCBBA	CCCBAB	CCCABB	CCBCBA	CCBCAB	CCBBCA	CCBBAC	CCBABC	CCBACB
CCABBC	CCABCB	CCACBB	CBCCBA	CBCCAB	CBCBCA	CBCBAC	CBCABC	CBCACB	CBBCCA
CBBCAC	CBBACC	CBACBC	CBACCB	CBABCC	CACBBC	CACBCB	CACCBB	CABCBC	CABCCB
CABBCC	BCCCBA	BCCCAB	BCCBCA	BCCBAC	BCCABC	BCCACB	BCBCCA	BCBCAC	BCBACC
BCACBC	BCACCB	BCABCC	BBCCCA	BBCCAC	BBCACC	BBACCC	BACCBC	BACCCB	BACBCC
BABCCC	ACCBBC	ACCBCB	ACCCBB	ACBCBC	ACBCCB	ACBBCC	ABCCBC	ABCCCB	ABCBCC

Перейдем теперь к сочетаниям.

Сочетанием из n элементов по m называется любое подмножество из m элементов, которое принадлежит множеству из n различных элементов.

Число сочетаний m объектов, выбранных из n без учета порядка, равно величине, имеющей специальное обозначение в математике:

. (5)

Величины 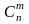, либо читаются: “число сочетаний m объектов, взятых из n”.

Отметим, что в среде MATLAB существует функция nchoosek(n,m), которая вычисляет число сочетаний m объектов из n при не слишком большом параметре n (n < 15).

Отметим, что размещения, перестановки и сочетания связаны друг с другом. Учитывая (1), (3), (5), можно записать:

.

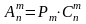При подсчете комбинаторных конфигураций используются следующие два простых правила.

• Правило суммы. Если некоторый объект A может быть выбран n способами, а объект B — m способами, то выбрать либо объект A, либо объект B можно n + m способами.

• Правило умножения. Если некоторый объект A может быть выбран n способами и после каждого такого выбора объект B можно выбрать m способами, то пара объектов (A,B) в указанном порядке может быть выбрана nm способами.