
- •Модуль 1 Елементи лінійної алгебри, вектори та аналітична геометрія. Вступ до математичного аналізу
- •1.1 Елементи лінійної алгебри
- •1.1.1 Поняття матриці . Визначники 2-го і 3-го порядків
- •1.1.2 Скалярний, векторний, змішаний добутки векторів, їх властивості та вираз через координати
- •1.2 Аналітична геометрія
- •1.2.1 Рівняння прямої на площині
- •1.2.2 Рівняння площини і прямої в просторі
- •1.3 Теорія границь
- •1.3.1 Поняття границі функції. Властивості границь
- •1.3.2 Розкриття невизначеностей
- •1.4 Диференціальне числення функцій однієї та декількох змінних
- •1.4.1 Похідна функції. Формули та правила диференціювання
- •1.4.2 Застосування похідних для дослідження функцій
- •1.4.3 Диференціальне числення функцій декількох змінних
- •Модуль 2 Невизначений, визначений і невласний інтеграли. Диференціальні рівняння. Кратні, криволінійні і поверхневі інтеграли
- •2.1 Інтегральне числення функцій однієї змінної
- •2.1.1 Неозначений інтеграл, його властивості. Основні методи інтегрування
- •2.1.2 Властивості визначеного інтеграла. Заміна змінного та інтегрування частинами
- •2.1.3 Невласні інтеграли
- •2.2 Диференціальні рівняння
- •2.2.1 Основні поняття. Диференціальні рівняння 1–го порядку: з відокремлюваними змінними, однорідні, лінійні
- •2.2.2 Диференціальні рівняння 2–го порядку
- •2.3 Інтегральне числення функцій декількох змінних
- •2.3.1 Кратні інтеграли
- •2.3.2 Криволінійні і поверхневі інтеграли
- •Модуль 3 Числові і функціональні ряди. Ряди Фур’є. Комплексні числа та аналітичність функцій комплексної змінної
- •3.1 Числові ряди
- •3.1.1 Необхідна і достатня ознаки збіжності рядів
- •3.1.2 Ряди з чергуванням знаків членів. Ознака Лейбніца.
- •3.2 Функціональні ряди
- •3.2.1 Степеневі ряди. Знаходження області збіжності рядів
- •3.2.2 Ряди Фур’є
- •Модуль 4 Теорія ймовірностей і елементи математичної статистики
- •4.1 Випадкові події. Класична та статистична ймовірності. Основні формули та теореми теорії ймовірностей
- •4.2 Випадкові величини. Закони розподілу
- •Література
2.1.2 Властивості визначеного інтеграла. Заміна змінного та інтегрування частинами
Обчислення
визначених інтегралів для
неперервної функції
полягає
в наступному: спочатку
знаходять
невизначений інтеграл (або первісну
![]() ),
а потім користуються
формулою
Ньютона-Лейбніца:
),
а потім користуються
формулою
Ньютона-Лейбніца:
![]() .
(2.1.7)
.
(2.1.7)
Приведемо без доведення основні властивості визначеного інтеграла:
1.
Якщо
![]() ,
то
,
то
![]() .
.
2.
![]() ,
де
- інтегрована на відрізку
,
де
- інтегрована на відрізку
![]() функція,
(
функція,
(![]() ).
).
3.
![]() .
.
4.
Якщо
функція
інтегрується на найбільшому з відрізків
,
![]() ,
,
![]() ,
то вона інтегрована на двох інших
відрізках, причому
,
то вона інтегрована на двох інших
відрізках, причому
![]() ,
,
де
![]() .
.
5.
Якщо
функція
інтегрована на відрізку
,
то функція
![]() ,
де
– постійне число, також інтегрована,
причому
,
де
– постійне число, також інтегрована,
причому
![]() .
.
6.
Якщо
функції
![]() ,
,
![]() ,
…,
,
…,
![]() інтегровані
на відрізку
,
то їх алгебраїчна сума також інтегрована,
причому
інтегровані
на відрізку
,
то їх алгебраїчна сума також інтегрована,
причому
![]() .
.
○ Приклад
2.1.5. Обчислити
інтеграли: а)
![]() ;
б)
;
б)
![]() .
.
Розв'язання.
а)
![]() ;
;
б)
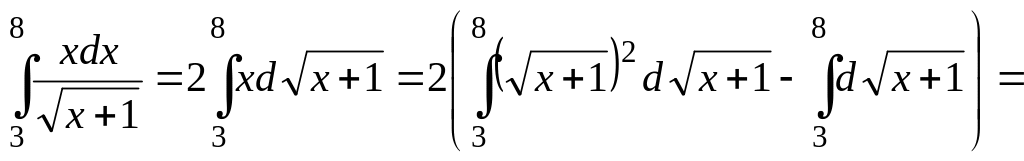
![]() .
●
.
●
Методи обчислення визначених інтегралів такі ж, як і при знаходженні невизначених інтегралів.
Метод
заміни змінної.
Якщо виконані умови: 1.
функція
неперервна на відрізку
;
2.
відрізок
є множиною значень функції
,
що визначена на відрізку
![]() і має на ньому неперервну похідну; 3.
і має на ньому неперервну похідну; 3.
![]() ,
,
![]() ,
то справедлива
формула
,
то справедлива
формула
![]() .
(2.1.8)
.
(2.1.8)
○ Приклад 2.1.6. Обчислити інтеграли:
а)
![]() ;
б)
;
б)
![]() .
.
Розв'язання.
а)
![]() ;
;
б)
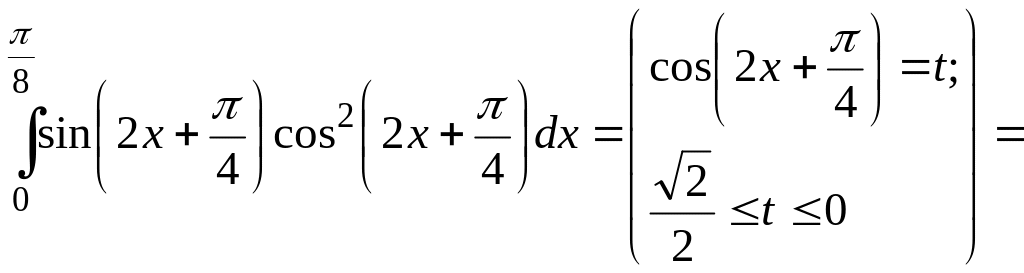
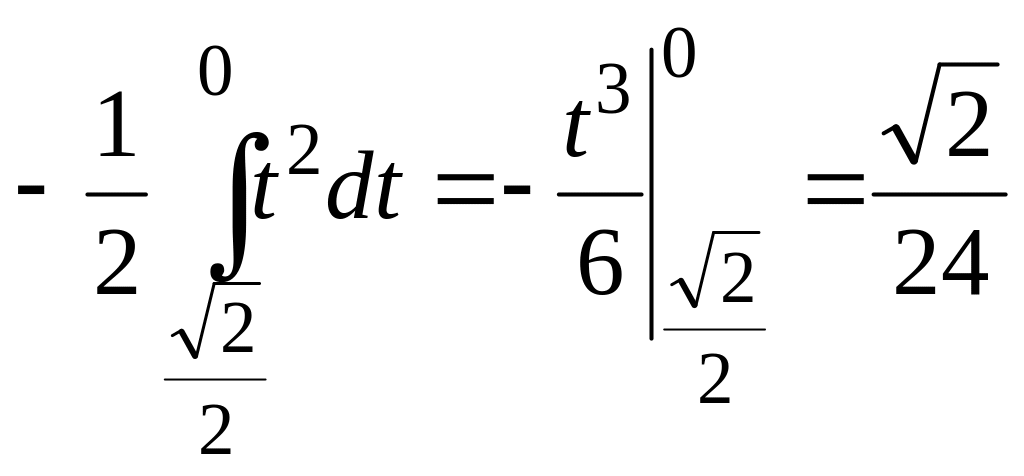 .
●
.
●
Метод інтегрування частинами. Якщо функції , мають неперервні похідні на відрізку , то справедлива формула
![]() .
(2.1.9)
.
(2.1.9)
○ Приклад
2.1.7. Обчислити
інтеграли: а)
 ;
б)
;
б)
![]() .
.
Розв'язання. а)
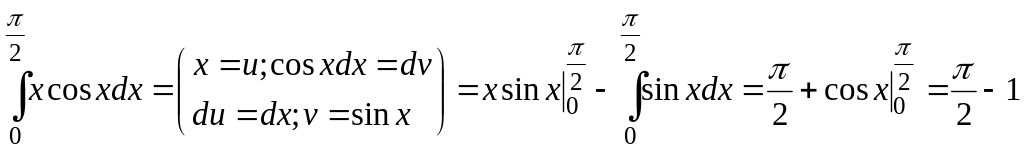 ;
;
б)
![]()
![]() .
●
.
●
2.1.3 Невласні інтеграли
Розрізняють невласні інтеграли I– го і II– го роду.
Невласними
інтегралами I–
го
роду
називаються
інтеграли з нескінченним проміжком
інтегрування
![]() (або
(або
![]() ,
або
,
або
![]() ),
які визначаються формулами:
),
які визначаються формулами:
![]() ;
(2.1.10)
;
(2.1.10)
![]() ;
(2.1.11)
;
(2.1.11)
![]() ,
(2.1.12)
,
(2.1.12)
Невласні інтеграли можуть мати як скінчене, так і нескінченне значення. Якщо границі не існують або дорівнюють нескінченності, то невласні інтеграли називаються тими, що розбігаються.
○ Приклад 2.1.8. Дослідити на збіжність інтеграли:
а)
![]() ;
б)
;
б)
![]() .
.
Розв'язання.
а)
![]()
![]() .
Інтеграл збігається і його значення
дорівнює 1;
.
Інтеграл збігається і його значення
дорівнює 1;
б)
![]()
![]()
![]() .
.
Оскільки границя не існує, то інтеграл розбігається. ●
Невласним
інтегралом II
–
го роду
від
функції
на
за умови, що
має розрив другого роду при
![]() називається інтеграл, що визначається
за формулою
називається інтеграл, що визначається
за формулою
 ,
(2.1.13)
,
(2.1.13)
де
![]() ,
,
![]() .
.
Інтеграл (2.1.13) збігається, якщо границі в (2.1.13) скінчені і існують. В протилежному випадку інтеграл є таким, що розбігається.
Якщо
підінтегральна функція має розрив II
–
го роду в точках
![]() або
або
![]() ,
то відповідні інтеграли II – го роду
обчислюються за формулами:
,
то відповідні інтеграли II – го роду
обчислюються за формулами:
![]() ,
(2.1.14)
,
(2.1.14)
![]() .
(2.1.15)
.
(2.1.15)
○ Приклад
2.1.9. Дослідити
на збіжність інтеграли: а)
![]() ;
б)
;
б)
![]() .
.
Розв'язання.
а)
![]() .
.
Інтеграл збігається;
б)
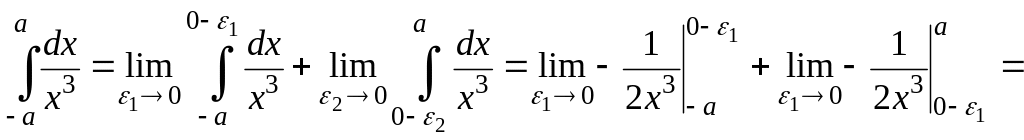
![]() .
.
Оскільки границя не існує, то інтеграл розбігається. ●
Література: [1, с. 173 – 195, 198-203], [2, с. 251 ‑ 312], [4, с. 284 – 341], [5].
