
- •Інститут економіки та нових технологій Кафедра прикладної математики та математичного моделювання
- •Наклад 200 примірників Передмова
- •І. Основні питання, що вивчаються в розділі „Диференціальні рівняння”.
- •Іі. Основні теоретичні відомості. Приклади розв’язання задач
- •1. Основні поняття. Задача Коші
- •2. Диференціальні рівняння 1-го порядку та способи їх розв’язання
- •Теорема 1 (Коші)
- •2.1. Диференціальні рівняння із змінними, які розділяються
- •Приклад 1
- •Розв’язання
- •Приклад 2
- •Розв’язання
- •2.2. Однорідні диференціальні рівняння.
- •Приклад 3
- •Розв’язання
- •Приклад 4
- •Розв’язання
- •2.3. Лінійні диференціальні рівняння.
- •3.1. Рівняння вигляду
- •3.2. Рівняння вигляду
- •3.3. Рівняння вигляду
- •Приклад 9
- •Розв’язання
- •Приклад 10
- •Розв’язання
- •4. Лінійні диференціальні рівняння другого порядку зі сталими коефіцієнтами
- •4.1. Однорідні лінійні диференціальні рівняння
- •4.2. Неоднорідні лінійні диференціальні рівняння другого порядку зі сталими коефіцієнтами та спеціальною правою частиною
- •Приклад 14
- •Розв’язання
- •Приклад 15
- •Розв’язання
- •Приклад 16
- •Розв’язання
- •5. Системи лінійних диференціальних рівнянь зі сталими коефіцієнтами
- •Приклад 17
- •Розв’язання
- •Ііі. Завдання для самостійної роботи
- •Іv. Завдання для контрольної роботи Завдання 1
- •Завдання 2
- •Завдання 3
- •Завдання 4
- •Завдання 5
- •Завдання 6
- •Завдання7
- •V. Список використаної і рекомендованої літератури
- •Завдання 1
- •Завдання 2
- •Завдання 3
Приклад 4
Розв’язати
рівняння:
![]() .
.
Розв’язання
Приведемо це рівняння до вигляду (2.2):
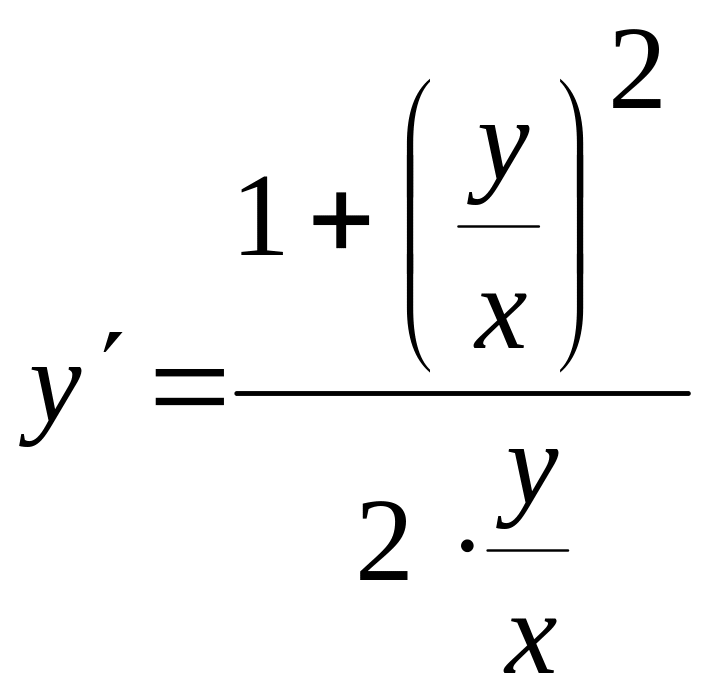 .
.
Замінимо:
![]() ,
,
![]() ,
.
,
.
Отримаємо
рівняння :
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Проінтегруємо:
![]() .
.
Маємо:
![]() .
(Якщо при розв’язуванні отримано
логарифми, зручно подати довільну сталу
інтегрування С
у вигляді логарифма
.
(Якщо при розв’язуванні отримано
логарифми, зручно подати довільну сталу
інтегрування С
у вигляді логарифма
![]() ).
).
Звідки:
![]()
![]() ,
,
![]() .
.
Повертаємось
до вихідних змінних:
![]() ,
тоді:
,
тоді:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Відповідь:
![]() .
.
Зауваження: Приклад 4 – зразок розв’язання завдання № 2.
2.3. Лінійні диференціальні рівняння.
Означення
5.
Лінійним диференціальним рівнянням
називається рівняння, що має
вигляд:
![]() (2.4)
(2.4)
де
![]() – функції, які залежать тільки від
змінної х.
– функції, які залежать тільки від
змінної х.
Метод
розв’язання: робимо заміну невідомої
функції:
![]() – деякі невідомі функції. Тоді
– деякі невідомі функції. Тоді
![]() .
.
Після заміни в рівнянні (2.4) маємо:
![]()
Далі виконуємо штучний крок: вважаємо невідому функцію v такою, що вираз у дужках (який завжди є множником до u та містить v и v/) має дорівнювати нулю:
![]() .
(2.5)
.
(2.5)
Враховуючи це, маємо, що для функції u виконується рівність:
![]() .
(2.6)
.
(2.6)
З
рівностей (2.5) і (2.6) знаходимо функції
![]() .
.
Приклад 5
Розв’язати
рівняння:
![]() .
.
Розв’язання
Виконавши
заміну:
![]() ,
маємо:
,
маємо:
![]() .
.
1.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
На цьому етапі довільну сталу С замінимо зручним значенням С=1 ( в інших випадках С=0 ). Отже, v = x.
2.
![]()
![]() .
.
а)
![]() ;
;
б)
![]() – інтегруємо за частинами, використовуючи
формулу:
– інтегруємо за частинами, використовуючи
формулу:
![]() .
.
![]()
Таким
чином,
![]()
3. Шукана
функція:
![]()
Відповідь:
![]()
Зауваження: приклад 5 – зразок розв’язання завдання №3.
3. Диференціальні рівняння другого порядку
3.1. Рівняння вигляду
Якщо
з рівняння можна виділити
![]() як функцію, залежну тільки від
х,
тобто
як функцію, залежну тільки від
х,
тобто
![]() ,
то розв’язок у=у(х)
знаходимо, інтегруючи ліву та праву
частини рівняння двічі.
,
то розв’язок у=у(х)
знаходимо, інтегруючи ліву та праву
частини рівняння двічі.
Приклад 7
Розв’язати
рівняння:
![]() .
.
Розв’язання
Запишемо
рівняння у вигляді:
![]() .
.
Знайдемо інтеграл:
![]()
![]()
![]() .
.
Відповідь: .
3.2. Рівняння вигляду
Якщо
рівняння містить
![]() та не містить в явному вигляді у,
то
метод розв’язування полягає в заміні:
та не містить в явному вигляді у,
то
метод розв’язування полягає в заміні:
![]()
Після такої заміни рівняння стає рівнянням 1-го порядку, розв’язання яких розглядались у п.2.2.-2.3.
Приклад 8
Розв’язати
рівняння:
![]() .
.
Розв’язання
Замінимо:
![]() .
.
Отримане
рівняння
![]() є рівнянням із змінними, що розділяються
(п.1.1.):
є рівнянням із змінними, що розділяються
(п.1.1.):
![]()
![]()
![]()
![]() ,
звідки
,
звідки
![]() .
.
Зворотна
заміна:
![]() ,
тобто
,
тобто
![]() ,
,
![]()
звідки
![]() – шукана функція.
– шукана функція.
3.3. Рівняння вигляду
Якщо
рівняння містить
![]() ,
та не містить в явному вигляді незалежну
змінну х,
то метод розв’язання полягає в наступному:
нехай
,
та не містить в явному вигляді незалежну
змінну х,
то метод розв’язання полягає в наступному:
нехай
![]() ,
тоді
,
тоді
![]() (оскільки
(оскільки
![]() ) (3.1.)
) (3.1.)
При цьому отримуємо диференціальне рівняння 1-го порядку, де невідомою функцією є р(у), а незалежною змінною – у.
Приклад 9
Знайти
загальний розв’язок диференціального
рівняння:
![]() .
.
Розв’язання
Згідно
з (3.1)
![]() ,
то рівняння матиме вигляд:
,
то рівняння матиме вигляд:
![]() .
.
При розв’язанні маємо:
![]() .
.
1.
![]() – знайшли частинний розв’язок рівняння.
– знайшли частинний розв’язок рівняння.
2.
![]() – це рівняння із змінними, що розділяються,
яке дасть нам загальний розв’язок
диференціального рівняння:
– це рівняння із змінними, що розділяються,
яке дасть нам загальний розв’язок
диференціального рівняння:

Оскільки
,
то
![]() – також із змінними, що розділяються,
тобто
– також із змінними, що розділяються,
тобто
![]()
![]()
![]() ,
звідки
,
звідки
![]() .
Підносимо обидві частини рівняння до
степеня
.
Підносимо обидві частини рівняння до
степеня
![]() ,
отримуємо розв’язок в явному вигляді
,
отримуємо розв’язок в явному вигляді
![]() або
або
![]() ,
де
,
де
![]()
![]() ,
,
![]()
![]() .
.
