8.1.4 Логарифмический частотный критерий Найквиста

Исходные данные – ЛАЧХ и ЛФЧХ разомкнутой системы.

Критерий устойчивости для 1 случая. Если разомкнутая система устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы ЛАЧХ разомкнутой системы пересекала ось частот (0 дБ) слева от частоты при которой ЛФЧХ пересекает линию .

Рисунок 8.9 – ЛАЧХ и ЛФЧХ устойчивой системы

8.2 Порядок выполнения работы

Лабораторная работа №8 состоит из трех частей, для выполнения которых необходимо использовать исходные данные из таблицы 6.5 (пункты 3 и 4). В дальнейшем примем, что в таблице 6.5. приведены передаточные функции разомкнутых систем. Под замкнутой системой будем понимать передаточные функции таблицы 6.5., замкнутые единичной отрицательной обратной связью.

1 часть. Используя критерий устойчивости Гурвица исследовать устойчивость разомкнутых систем и замкнутых систем.

2 часть. Используя критерий Михайлова:

– построить годограф Михайлова;

– исследовать устойчивость разомкнутых и замкнутых систем при различных значениях коэффициентов усиления и постоянных времени;

– построить переходной процесс для установления зависимости между частотными и временными характеристиками.

3 часть. Используя критерий Найквиста:

– построить временные характеристики и АФЧХ устойчивых разомкнутых систем (значения коэффициента усиления и постоянных времени выбираются произвольно) и показать при каких параметрах разомкнутых систем, замкнутая система будет находиться в состояниях: устойчивости, неустойчивости, на границе устойчивости. Временные характеристики строятся для подтверждения состояния разомкнутой системы.

– построить временные характеристики и АФЧХ неустойчивых разомкнутых систем, (значения коэффициента усиления и постоянных времени выбираются произвольно) и показать при каких параметрах разомкнутых систем, замкнутая система будет находиться в состояниях: устойчивости, неустойчивости, на границе устойчивости;

– построить временные характеристики и АФЧХ (без использования программы MATLAB) разомкнутых систем на границе устойчивости и показать при каких параметрах разомкнутых систем, замкнутая система будет находиться в состояниях: устойчивости, неустойчивости, на границе устойчивости.

5. Сделать выводы по каждому из этапов выполненной работы.

8.3 Методический пример выполнения лабораторной работы №8

1 часть. Алгебраическим критерием Гурвица исследуем на устойчивость разомкнутую и замкнутую систему

, . (8.4)

Построим матрицу Гурвица разомкнутой и замкнутой систем (8.4)

, . (8.5)

Для реализации критерия Гурвица используем CST MATLAB. Разобьем матрицы Гурвица (8.5) на диагональные миноры и найдем их определители:

– для разомкнутой системы

>> G22=[0.3 0.1;1 0.5]

G22 =

0.3000 0.1000

1.0000 0.5000

>> det(G22)

ans = 0.0500

>> G33=[0.3 0.1 0;1 0.5 0;0 0.3 0.1]

G33 =

0.3000 0.1000 0

1.0000 0.5000 0

0 0.3000 0.1000

>> det(G33)

ans = 0.0050

–для замкнутой системы

>> G22=[0.3 10.1;1 0.5]

G22 =

0.3000 10.1000

1.0000 0.5000

>> det(G22)

ans =

–9.9500

>> G33=[0.3 10.1 0;1 0.5 0;0 0.3 10.1]

G33 =

0.3000 10.1000 0

1.0000 0.5000 0

0 0.3000 10.1000

>> det(G33)

ans =

–100.4950

Вывод: При сравнительном анализе значений определителей главных диагональных миноров матрицы Гурвица со знаком элемента , в соответствии с критерием Гурвица разомкнутая система устойчива, а замкнутая система не устойчива.

2 часть. Частотным критерием Михайлова исследуем на устойчивость разомкнутую САУ

.

Для этого получим выражение для действительной Re() и мнимой Im() составляющих комплексного характеристического полинома (8.3). Построим в MATLAB Simulink схемы блоков Re() и Im() как функций на основе математических операционных блоков Math Operation и блока подачи возрастающего сигнала Ramp (рисунок 8.10).

Для сравнения снимается переходная характеристика системы.

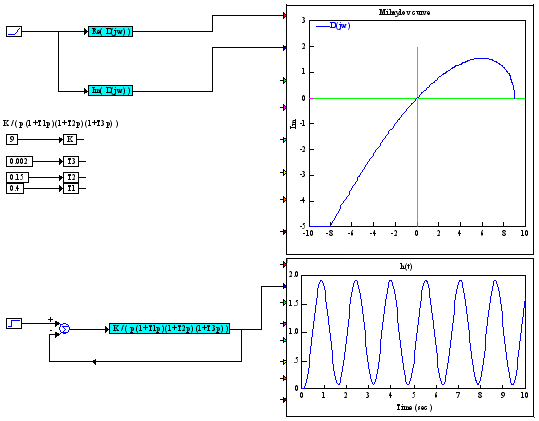
Рисунок 8.10 – Переходная характеристика и годограф Михайлова

Вывод: В соответствии с частотным критерием Михайлова можно сделать вывод, что разомкнутая система находится на границе устойчивости.

3 часть. Частотный критерий Найквиста.

1 этап. Построение временных характеристик и АФЧХ устойчивых разомкнутых систем.

а)

б)

в)

г)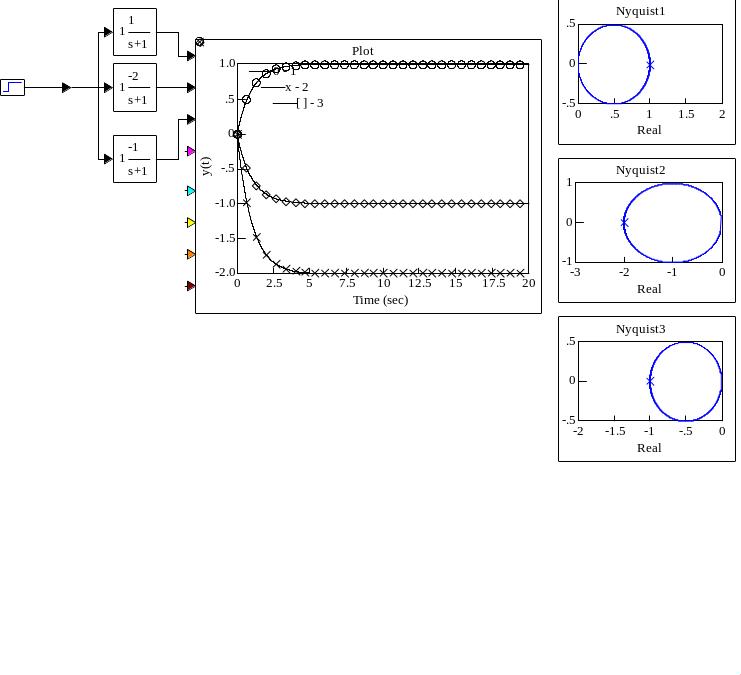

а) переходные характеристики устойчивых разомкнутых САУ; б) АФЧХ устойчивой замкнутой САУ; в) АФЧХ неустойчивой замкнутой САУ; г) АФЧХ замкнутой САУ на границе устойчивости

Рисунок 8.11 – Устойчивые разомкнутые САУ

2 этап. Построение переходных характеристик и АФЧХ неустойчивых разомкнутых систем.

а)

б)

в)

г)

а) переходные характеристики неустойчивых разомкнутых САУ; б) АФЧХ устойчивой замкнутой САУ; в) АФЧХ неустойчивой замкнутой САУ; г) АФЧХ замкнутой САУ на границе устойчивости

Рисунок 8.12 – Неустойчивые разомкнутые САУ

3 этап. Построение временных характеристик и АФЧХ (без использования программы Vissim) разомкнутых систем на границе устойчивости.

Рисунок 8.13 – Переходные характеристики разомкнутых САУ

на границе устойчивости