
Министерство образования и науки РФ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
ТОСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра компьютерных систем
в управлении и проектировании (КСУП)
Практическая работа №2
По дисциплине
«Теория вероятностей, математическая статистика и случайные процессы»
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Выполнил:
Студент гр. 511
_______ А.Н. Дисенко
«__»________2012
Проверил:
Доцент каф. КСУП
Канд. Техн. наук
______ М. И. Андреев
«__»________2012
2012
Задание
Практика №2
Вариант №10
Задача №1
Является ли случаем следующая группа событий: опыт – бросание двух монет; события: A1 – появление двух гербов; A2 – появление двух цифр; A3 – появление одного герба и одной цифры?
Задача №2
В монтажном цехе к устройству присоединяется электродвигатель. Электродвигатели поставляются тремя заводами – изготовителями. На складе имеются электродвигатели названных заводов соответственно в количестве 19, 6 и 11шт., которые могут безотказно работать до конца гарантийного срока соответственно с вероятностями 0,85, 0,76 и 0,71. Рабочий берет случайно один двигатель и монтирует его к устройству. Найти вероятности того, что смонтированный и работающий безотказно до конца гарантийного срока электродвигатель поставлен третьим заводом изготовителем.
Задача №3
Наудачу взяты два положительных числа x и y, каждое из которых не превышает двух.
Найти вероятность того, что произведение xy будет не больше единиц, а частное y/x не больше двух.
Задача №4
В лотерее разыгрываются крупные и мелкие выйгрыши.
Вероятность того, что на лотерейный билет выпадет выйгрыш равна 0,001, а мелкий – 0,01.
Куплено 1000 билетов. Найти вероятность того, что крупных выйгрышей будет два.
Задача №5
Бросают три игральные кости.
Составить закон распределения дискретной случайной величины X – число игральных костей, на верхних гранях которых появятся только четные числа очков.
К какому типу распределений относится полученный закон?
Задача №6
Найти математическое ожидание дискретной случайной величины Z, если известны математические ожидания X и Y: Z=3X+4Y, M(X) = 2, M(Y)=6.
Задача №7
Найти дисперсию дискретной случайной величины X, заданной законом распределения:
Х |
-3 |
1 |
2 |
3 |
p |
0,4 |
0,3 |
0,1 |
0,2 |
Задача №8
Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1.
Найти среднеквадратическое отклонение дискретной случайной величины X – числа отказавших элементов в одном опыте
Содержание
1 Введение 5
2 Решение задачи №1 6
3 Решение задачи №2 7
4 Решение задачи №3 9
5 Решение задачи №4 10
6 Решение задачи №5 11
7 Решение задачи №6 13
8 Решение задачи №7 14
9 Решение задачи №8 15
10 Блок схема программы 17
13 Разработка алгоритма решения задачи №8 18
14 Разработка пргораммы решения решения подкласса задач,
к которому относится задача №8 18
16 Методика тестирования разработанной программы 19
17 Руководство пользоватея 19
18 Заключение 20
Список использованных источников 21
Приложение А 22
1 Введение
Цель работы: изучение раздела «Случайные величины». Вывод общих формул и применение их на практике при анализе и решении различных задач данного раздела. Результаты работы могут широко применятся на практике, а так же в сферах жизнедеятельности при различных обстоятельствах.
2 Решение задача №1
Является ли случаем следующая группа событий: опыт – бросание двух монет; события: A1 – появление двух гербов; A2 – появление двух цифр; A3 – появление одного герба и одной цифры?
Анализ и классификация задачи
Задача относится к разделу «Классическое определение вероятностей», так как в ней идет речь нахождении вероятности появления событий A1, A2, и A3 и определения являетсяли данная група случаем в опыте с бросанием монеты.
Обоснование метода решения задачи
Так как в задаче необходимо найти вероятность попадания по мишени или промаха и определить равновозможными данные события, то нужно воспользоваться классической формулой нахождения вероятности события:

 ,
,
где n - общее количество исходов опыта, m - исходы, благоприятные событию A.
Пошаговый алгоритм решения задачи
Шаг 1. Применить формулу для вероятности.
Шаг 2. Сравнить вероятность каждого из событий.
Шаг 3. Получить ответ.
Решение
Так как случаем являются события, которые образуюют полную группу, являются несовместными и равновозможными, то нужно проверить выполнение всех условий определения. Первое и второе условия выполняются (по определению), осталось проверить выполнение третьего условия, т.е. определить являются ли события равновозможными.
Введём следующие обозначения для событий: A1- появление двух гербов, A2 – появление двух цифр A3 – появление одного герба и одной цифры.
Рассмотрим основные исходы опыта при бросании монеты два раза:
1) Герб, герб; 2) Герб, цифра; 3) Цифра, герб; 4) Цифра, цифра.
Первый исход опыта соответсвует событию A1, второй и третий – событию A3, четвертый – событию A2. Применяя формулу вероятности вычислим вероятность появления каждого из событий:
P(A1)
=
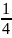 = 0,25; P(A2)
=
= 0,25; P(A3)
=
= 0,25; P(A2)
=
= 0,25; P(A3)
=
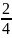 = 0,5.
= 0,5.
Так как вероятность появления события A3 не равно вероятности появления событий A1 и A2, то данные события не являются равновозможными, а значит группа событий не образуют случай.
Ответ: группа событий A1, A2 и A3 не является случаем.
3 Решение задача №2
В монтажном цехе к устройству присоединяется электродвигатель. Электродвигатели поставляются тремя заводами – изготовителями. На складе имеются электродвигатели названных заводов соответственно в количестве 19, 6 и 11шт., которые могут безотказно работать до конца гарантийного срока соответственно с вероятностями 0,85, 0,76 и 0,71. Рабочий берет случайно один двигатель и монтирует его к устройству. Найти вероятности того, что смонтированный и работающий безотказно до конца гарантийного срока электродвигатель поставлен третьим заводом изготовителем.
Анализ и классификация задачи
Задача относится к разделу «Отношение между вероятностями событий», так как в ней идет речь о нахождении вероятности события с условием (В3|А), в опыте с выбором электродвигателя поставленного некоторым.
Обоснование метода решения задачи
Для нахождения искомой вероятности нужно воспользоваться формулой Байеса:
 =
=
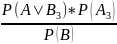 ,
,
где
– Вероятность события B3,
при условии, что произошло событие A3,
 – условная вероятность события A,
– условная вероятность события A,
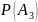 - вероятность события A3,
P(B)
– полная вероятность событий.
- вероятность события A3,
P(B)
– полная вероятность событий.
Пошаговый алгоритм решения задачи
Шаг 1. Рассмотреть следующие события:
A1 – (выбранный э/д поставлен 1 заводом изготовителем);
A2 – (выбранный э/д поставлен 2 заводом изготовителем);
A3 – (выбранный э/д поставлен 3 заводом изготовителем).
Шаг 2. Применить классическую формулу нахождения для всех событий.
Шаг 3. Вычислить полную вероятность вышеперечисленных событий.
Шаг 4. Подставить полученные вероятности в формулу Байеса.
Шаг 5. Получить ответ.
Решение
Первым испытанием является выбор электродвигателя, вторым – работа электродвигателя во время гарантийного срока. Рассмотрим следующие события:
A1 – (выбранный э/д поставлен 1 заводом изготовителем);
A2 – (выбранный э/д поставлен 2 заводом изготовителем);
A3 – (выбранный э/д поставлен 3 заводом изготовителем).
P(A1)
=
 = 0,527 ; P(A2)
=
= 0,527 ; P(A2)
=
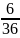 = 0,166 ; P(A3)
=
= 0,166 ; P(A3)
=
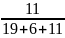 =
=
 = 0,305
= 0,305
Условные вероятности заданы в условии задачи: P(A|B3) = 0,71, P(A|B2) = 0,76, P(A|B1) = 0,85.
Вычисляем полную вероятность:
Р(B) = 0,85 × 0,527 + 0,76 × 0,166 + 0,71 × 0,305 = 0,7906.
По
формуле Байеса вычисляем условные
вероятности событий (гипотез): Р(В3|А)
=
 =
0,273.
=
0,273.
Ответ: вероятность того, что смонтированный и работающий безотказно до конца гарантийного срока электродвигатель поставлен третьим заводом изготовителем составляет 0,273.
4 Решение задача №3
Наудачу взяты два положительных числа x и y, каждое из которых не превышает двух.
Найти вероятность того, что произведение xy будет не больше единиц, а частное y/x не больше двух.
Анализ и классификация задачи
Задача относится к разделу «геометрическое определение вероятности событий», так как в ней идёт речь о нахождении вероятности события того, что произведение xy<1, а частное x/y<2, в опыте с наудучу взятыми двумя положительными числам.
Обоснование метода решения задачи
Так как в задаче необходимо найти вероятность события A: при выборе двух положительных чисел их произведение xy<1, а частное x/y<2, то нужно воспользоваться формулой геометрической вероятности:
P(A)=S1/S2 ,
где S1 и S2 – площади геом. фигур.
Пошаговый алгоритм решения задачи
Шаг 1. Находим площадь области всех допустимых значений.
Шаг 2. Находим площадь области всех значений, удовлетворяющих условию.
Шаг 3. Подставляем найденные величины в формулу геометрической вероятности.
Шаг 4. Получить ответ.
Решение
Определим область допустимых значений. Так как x<2 и y<2, x>0 и y>0, то областью допустимых значений будет квадрат размерами 2×2. Найдём площадь области допустимых значений S1=4.
Определим область значений удовлетворяющих условию. Так как по условию xy<1 и x/y<2, то данная область будет ограничена областью удовлетворяющей данным уравнениям и областью допустимых значений.
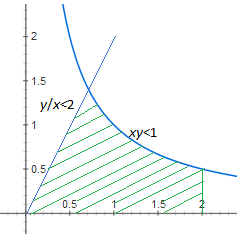
Найдём
площадь области значений удовлетворяющих
условию. Сначало решим систему урвнений
xy<1
и x/y<2
и найдем точку пересечения функций и
относительно неё найдем общую площадь.
Точка пересечения функций x=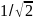 . Площадь области значений удовлетворяющих
условию S2=
. Площадь области значений удовлетворяющих
условию S2= = 1/2 + ln
2 – ln
= 1,539.
= 1/2 + ln
2 – ln
= 1,539.
Находим вероятность события A, подставляя найденные величины в формулу геометрической вероятности: P(A) = 1,539/4 = 0,38.
Ответ: P(A) = 0,38.
5 Решение задача №4
В лотерее разыгрываются крупные и мелкие выйгрыши.
Вероятность того, что на лотерейный билет выпадет выйгрыш равна 0,001, а мелкий – 0,01.
Куплено 1000 билетов.
Найти вероятность того, что крупных выйгрышей будет два.
Анализ и классификация задачи
Задача относится к разделу «определение вероятности», так как в ней требуется вычислить вероятность выйгрыша в лотерее.
Обоснование метода решения задачи
Так как вероятность выйгрыша p мала, а число купленных билетов n велико, то необходимо применить формулу распределения Пуассона:
Pn(m)
≈
 ,
,
где 𝜆 = pn, m – число благоприятных исходов события.
Пошаговый алгоритм решения задачи
Шаг 1. Находим 𝜆 – среднее число крупных выйгрышей.
Шаг 2. Подставляем все величины в формулу и находим вероятность события, если число благоприятных исходов равно двум.
Шаг 3. Получаем ответ.
Решение
Находим среднее число крупных выйгрышей:
𝜆 = 0,001 × 1000 = 1.
Находим вероятность события, когда число исходов равно двум:
P1000(2)
≈
 ≈ 0,183.
≈ 0,183.
Ответ: P1000(2) ≈ 0,183.
6 Решение задача №5
Бросают три игральные кости.
Составить закон распределения дискретной случайной величины X – число игральных костей, на верхних гранях которых появятся только четные числа очков.
К какому типу распределений относится полученный закон?
Анализ и классификация задачи
Задача относится к разделу «дискретная случайная величина», так как в ней требуется составить закон распределения дискретной случайной величины.
Обоснование метода решения задачи
Для составления закона распределения дискретной случайной величины необходимо рассмотреть случайную величину X и для каждого случая вычислить вероятность возможного значения X = k (числа k появления события) по формуле Бернулли:
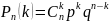 ,
,
где n – число независимых испытаний, p – вероятность появления события, q = 1-p.
Пошаговый алгоритм решения задачи
Шаг 1. Определим случаи, которые может принять величена X.
Шаг 2. Находим вероятности возможного значения для каждого случая по формуле Бернулли.
Шаг 3.Составим закон распределения дискретной величины X.
Решение
Пусть X -числа появлений четных чисел на верхних гранях трёх игральных костей при их бросаниях. X может принять значения 0,1,2,3.
Вероятность появления четного числа на верхней грани игральной кости, при каждом её бросании p = 3/6 = 0.5.
Применим формулу Бернулли - нахождения вероятности возможного значения для каждого случая.
P(X
= 0) = P3(0)
=
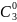 ×
0,50
× 0,53
= 0,125;
×
0,50
× 0,53
= 0,125;
P(X
= 1) = P3(1)
=
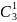 ×
0,51
× 0,52
= 0,375;
×
0,51
× 0,52
= 0,375;
P(X
= 2) = P3(2)
=
 ×
0,52
× 0,51
= 0,375;
×
0,52
× 0,51
= 0,375;
P(X
= 3) = P3(3)
=
 ×
0,53
× 0,50
= 0,125.
×
0,53
× 0,50
= 0,125.
Искомый закон распределения имеет вид:
Х |
0 |
1 |
2 |
3 |
p |
0,125 |
0,375 |
0,375 |
0,125 |
Многоугольник распределения имеет вид:
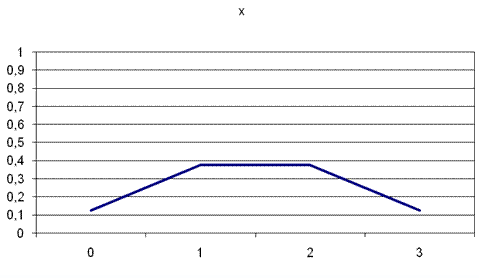
Полученный закон относится к типу дискретной конечной случайной величины, так как в задаче случайная величина принимает конечное число значений 0, 1, 2, 3.
Ответ: Искомый закон распределения имеет вид:
Х |
0 |
1 |
2 |
3 |
p |
0,125 |
0,375 |
0,375 |
0,125 |
7 Решение задача №6
Найти математическое ожидание дискретной случайной величины Z, если известны математические ожидания X и Y: Z=3X+4Y, M(X) = 2, M(Y)=6.
Анализ и классификация задачи
Задача относится к разделу «числовые характеристики случайных величин», так как в ней требуется найти математическое ожидание дискретной случайной величины Z.
Обоснование метода решения задачи
Для нахождения математического ожидания дискретной случайной величины Z необходимо использовать свойства математического ожидания.
Пошаговый алгоритм решения задачи
Шаг 1. Вычислим математическое ожидание дискретной случайной величины Z используя его свойство суммы и поятоянного множителя.
Шаг 2. Получим ответ.
Решение
Используя свойства математического ожидания (математическое ожидание суммы равно сумме математических ожиданий слагаемых; постоянный множитель можно вынести за знак математического ожидания), получим:
M(Z) = M(3X + 4Y) = M(3X) + M(4Y) = 3M(X) + 4M(Y) = 3×2 + 4×6 = 30.
Ответ: M(Z) =30.
8 Решение задача №7
Найти дисперсию дискретной случайной величины X, заданной законом распределения:
Х |
-3 |
1 |
2 |
3 |
p |
0,4 |
0,3 |
0,1 |
0,2 |
Анализ и классификация задачи
Задача относится к разделу «числовые характеристики случайных величин», так как в ней требуется найти дисперсию дискретной случайной величины X.
Обоснование метода решения задачи
Для нахождения дисперсии дискретной случайной величины X нужно воспользоваться теоремой: Дисперсия равна разности между математическим ожиданием квадрата случайной величины X и квадратом ее математического ожидания:
D (X) = М (X2) — [M (X)]2.
Пошаговый алгоритм решения задачи
Шаг 1. Найдем математическое ожидание М (X);
Шаг 2. Составим закон распределения случайной величины X2;
Шаг 3. Найдем математические ожидания М (X2);
Шаг 4. Подставим найденные величины в формулу дисперсии дискретной случайной величины.
Шаг 5. Получим ответ.
Решение
Найдем математическое ожидание М (X):
М (Х) = -3 × 0,4 + 1 × 0,3 + 2 × 0,1 + 3 × 0,2 = -0,1
Напишем закон распределения случайной величины X2:
Х2 |
9 |
1 |
4 |
9 |
p |
0,4 |
0,3 |
0,1 |
0,2 |
Найдем математические ожидания М (X2):
M(X2) = 9 × 0,4 + 1 × 0,3 + 4 × 0,1 + 9 × 0,2 = 6,1
Подставляя найденные величины в формулу дисперсии дискретной случайной величины, получим:
D(X) = М (X2) - [М (Х)]2 = 6,1 - (-0,1)2 = 6,09.
Ответ: D(X) = 6,09.
9 Решение задачи №8
Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1.
Найти среднеквадратическое отклонение дискретной случайной величины X – числа отказавших элементов в одном опыте.
Анализ и классификация задачи
Задача относится к разделу «числовые характеристики случайных величин», так как в ней требуется найти среднеквадратическое отклонение дискретной случайной величины X.
Обоснование метода решения задачи
Для нахождения среднеквадратического отклонения дискретной случайной величины X необходимо воспользоваться формулой:
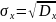 ,
,
где
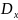 - дисперсия дискретной случайной величины
X.
- дисперсия дискретной случайной величины
X.
Пошаговый алгоритм решения задачи
Шаг 1. Составим закон распределения дискретной величины X.
Шаг 2. Найдем дисперсию дискретной случайной величины X.
Шаг 3. Вычислим по формуле среднеквадратическоое отклонение дискретной случайной величины X.
Шаг 4. Получим ответ.
Решение
Дискретная случайная величина X (число откозавших элементов в одном опыте) имеет следующие возможные значения: x1 = 0 (ни один из элементов устройства не отказал), x2 = 1 (отказал один элемент), x3 = 2 (откозали два элемента), x3 = 3 (отказали три элемента).
Отказы элементов независимы друг от друга, вероятности отказа
каждого элемента равны между собой, поэтому применима формулу Бернулли:
,
где n – число независимых испытаний, p – вероятность появления события, q = 1-p.
Учитывая, что, по условию, n = 3, p = 0,1, получим:
P(X = 0) = P3(0) = × 0,10 × 0,93 = 0,729;
P(X = 1) = P3(1) = × 0,11 × 0,92 = 0,243;
P(X = 2) = P3(2) = × 0,12 × 0,91 = 0,027;
P(X = 3) = P3(3) = × 0,13 × 0,90 = 0,001.
Запишим искомый закон распределения X:
Х |
0 |
1 |
2 |
3 |
p |
0,729 |
0,243 |
0,027 |
0,001 |
Найдем математическое ожидание М (X):
М (Х) = 0 × 0,729 + 1 × 0,243 + 2 × 0,027 + 3 × 0,001 = 0,3
Напишем закон распределения случайной величины X2:
Х2 |
0 |
1 |
4 |
9 |
p |
0,729 |
0,243 |
0,027 |
0,001 |
Найдем математические ожидания М (X2):
M(X2) = 0 × 0,729 + 1 × 0,243 + 4 × 0,027 + 9 × 0,001 = 0,36
Подставляя найденные величины в формулу дисперсии дискретной случайной величины, получим:
D(X) = М (X2) - [М (Х)]2 = 0,36 - (0,3)2 = 0,27.
Подставляя значение дисперсии в формулу
среднеквадратическоое отклонение
дискретной случайной величины X
получим:
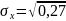 = 0,519.
= 0,519.
Ответ: :
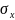 = 0,519.
= 0,519.
10 Блок схема программы
Реализуем блок-схему для правильно работы программы:

