
- •Киров 2006
- •Рецензент: к.Т.Н., доцент каф. Эвм Матвеева л.И.
- •1 Оформление лабораторной работы
- •1.1 Цель работы
- •1.2 Формирование отчета
- •2 Общие принципы методов поиска безусловного экстремума
- •3 Методы нулевого порядка
- •3.1 Метод конфигураций (метод Хука - Дживса)
- •3.2 Метод деформируемого многогранника
- •3.3 Метод вращающихся координат (метод Розенброка)
- •3.4 Метод сопряженных направлений (метод Пауэлла)
- •4 Методы первого порядка
- •4.1 Метод градиентного спуска с постоянным шагом
- •4.2 Метод наискорейшего градиентного спуска (Метод Коши)
- •4.3 Метод Гаусса - Зейделя
- •4.4 Метод сопряженных градиентов (Флетчера – Ривса)
- •5 Методы второго порядка
- •5.1 Метод Ньютона
- •5.2 Метод Ньютона - Рафсона
- •5.3 Метод Марквардта
- •6 Пример отчета по лабораторной работе
- •7 Блок вариантов заданий
- •8 Библиографический список
5 Методы второго порядка
Методы второго порядка служат для решения задач, общая постановка задач которых следующая: дана функция , ограниченная снизу на множестве и имеющая непрерывные частные производные первого и второго порядков во всех его точках. Требуется найти локальный минимум функции на множестве допустимых решений , т.е. найти такую точку , что
![]() .
.
5.1 Метод Ньютона
Стратегия
метода Ньютона состоит в построении
последовательности точек
![]() ,
таких, что
,
таких, что
![]() Точки
последовательности вычисляются по
правилу
Точки
последовательности вычисляются по
правилу
![]()
где
![]() -
задается пользователем, а направление
спуска
-
задается пользователем, а направление
спуска
![]() определяется
для каждого значения k
по формуле
определяется
для каждого значения k
по формуле
![]() (8)
(8)
Выбор
по
формуле (8) гарантирует выполнение
требования
![]() при условии, что
при условии, что
![]() .
Формула (8) получена из следующих
соображений:
.
Формула (8) получена из следующих
соображений:
1.
Функция f(x)
аппроксимируется в каждой точке
последовательности
![]() квадратичной функцией
квадратичной функцией
![]()
2.
Направление
определяется
из необходимого условия экстремума
первого порядка:
![]() Таким
образом, при выполнении требования
последовательность
является последовательностью точек
минимумов квадратичных функций
Таким
образом, при выполнении требования
последовательность
является последовательностью точек
минимумов квадратичных функций
![]() (рис.5.1).
(рис.5.1).
Чтобы
обеспечить выполнение требования
,
даже в тех случаях, когда для каких-либо
значений матрица Гессе
![]() не
окажется положительно определенной,
рекомендуется для соответствующих
значений k
вычислить точку
не
окажется положительно определенной,
рекомендуется для соответствующих
значений k
вычислить точку
![]() по методу градиентного спуска
по методу градиентного спуска
![]() с
выбором величины шага
с
выбором величины шага
![]() из условия
из условия
![]() .
.
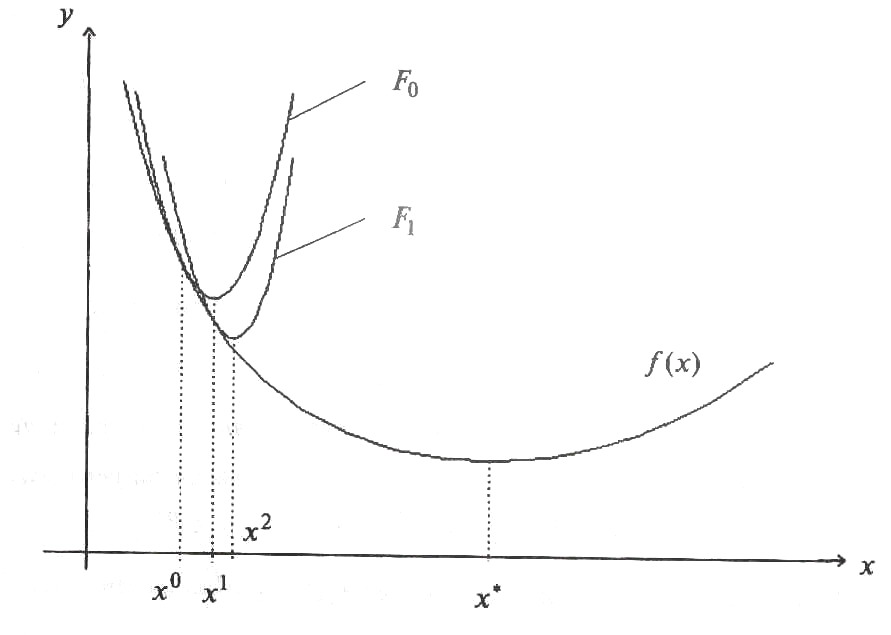
Рисунок 5.1.
Построение
последовательности
заканчивается в точке
![]() ,
для которой
,
для которой
![]() ,
где
,
где
![]() -
заданное малое положительное число,
или при
-
заданное малое положительное число,
или при
![]() (М
– предельное число итераций), или при
двукратном одновременном выполнении
двух неравенств
(М
– предельное число итераций), или при
двукратном одновременном выполнении
двух неравенств
![]() ,
где
,
где
![]() -малое
положительное число.
-малое
положительное число.
Утверждение:
Пусть f(x)
дважды непрерывно дифференцируемая
сильно выпуклая функция с константой
l>0
на
![]() и удовлетворяет условию
и удовлетворяет условию
![]()
где
L>0,
а начальная точка такова, что
![]() ,
т.е.
,
т.е.
![]() ,
,
где
![]() .
Тогда последовательность
сходится к точке минимума с квадратичной
скоростью
.
Тогда последовательность
сходится к точке минимума с квадратичной
скоростью
![]()
Алгоритм:
Шаг
1. Задать
![]() ,
М
– предельное число итераций. Найти
градиент
,
М
– предельное число итераций. Найти
градиент
![]() и
матрицу Гессе
и
матрицу Гессе
![]() .
.
Шаг 2. Положить k = 0.
Шаг
3. Вычислить
![]() .
.
Шаг
4. Проверить
выполнение критерия окончания
![]() :
:
а)
если неравенство выполнено, то расчет
окончен и
![]() ;
;
б) в противном случае перейти к шагу 5.
Шаг 5. Проверить выполнение неравенства :
а) если неравенство выполнено, то расчет окончен и ;
б) в противном случае перейти к шагу 6.
Шаг 6. Вычислить матрицу .
Шаг
7. Вычислить
матрицу
![]() .
.
Шаг
8. Проверить
выполнение условия
![]() :
:
а) если , то перейти к шагу 9;
б)
если нет, то перейти к шагу 10, положив
![]() .
.
Шаг
9. Определить
![]() .
.
Шаг
10. Найти
точку
![]() ,
,
положив =1, если ,
или выбрав из условия , если .
Шаг 11. Проверить выполнение условий
:
а)
если оба условия выполнены при текущем
значении k
и k
= k
- 1, то расчет
окончен,
![]() ;
;
б) в противном случае положить k = k + 1 и перейти к шагу 3.
Пример: Методом Ньютона найти локальный минимум функции
Решение:
1. Зададим , M: , , M =10.
Найдем
градиент функции в произвольной точке
и матрицу Гессе
![]() .
.
2. Положим k = 0.
30. Вычислим : .
40. Проверим условие : .
50. Проверим условие : .
60.
Вычислим
![]() :
:![]() .
.
70.
Вычислим
![]() :
: .
.
80.
Проверим выполнение условия
![]() .
Т.к.
.
Т.к.
![]() ,
то согласно критерию Сильвестра
.
,
то согласно критерию Сильвестра
.
90.
Определим
 .
.
100.
Вычислим
![]() .
.
110. Проверим условия: :
![]() .
.
Полагаем k = 1, переходим к шагу 3.
31.
Вычислим
:
![]() .
.
41.
Проверим
условие
:
![]() .
.
Расчет
окончен. Найдена точка
![]() .
.
Проанализируем полученную точку:
Функция
является строго выпуклой, т.к. ее матрица
вторых производных
![]() в силу того, что
в силу того, что
![]() .
Найденная точка
.
Найденная точка
![]() есть точка локального и одновременно
глобального минимума функции.
есть точка локального и одновременно
глобального минимума функции.
Решение задачи представлено на рисунке 5.2.
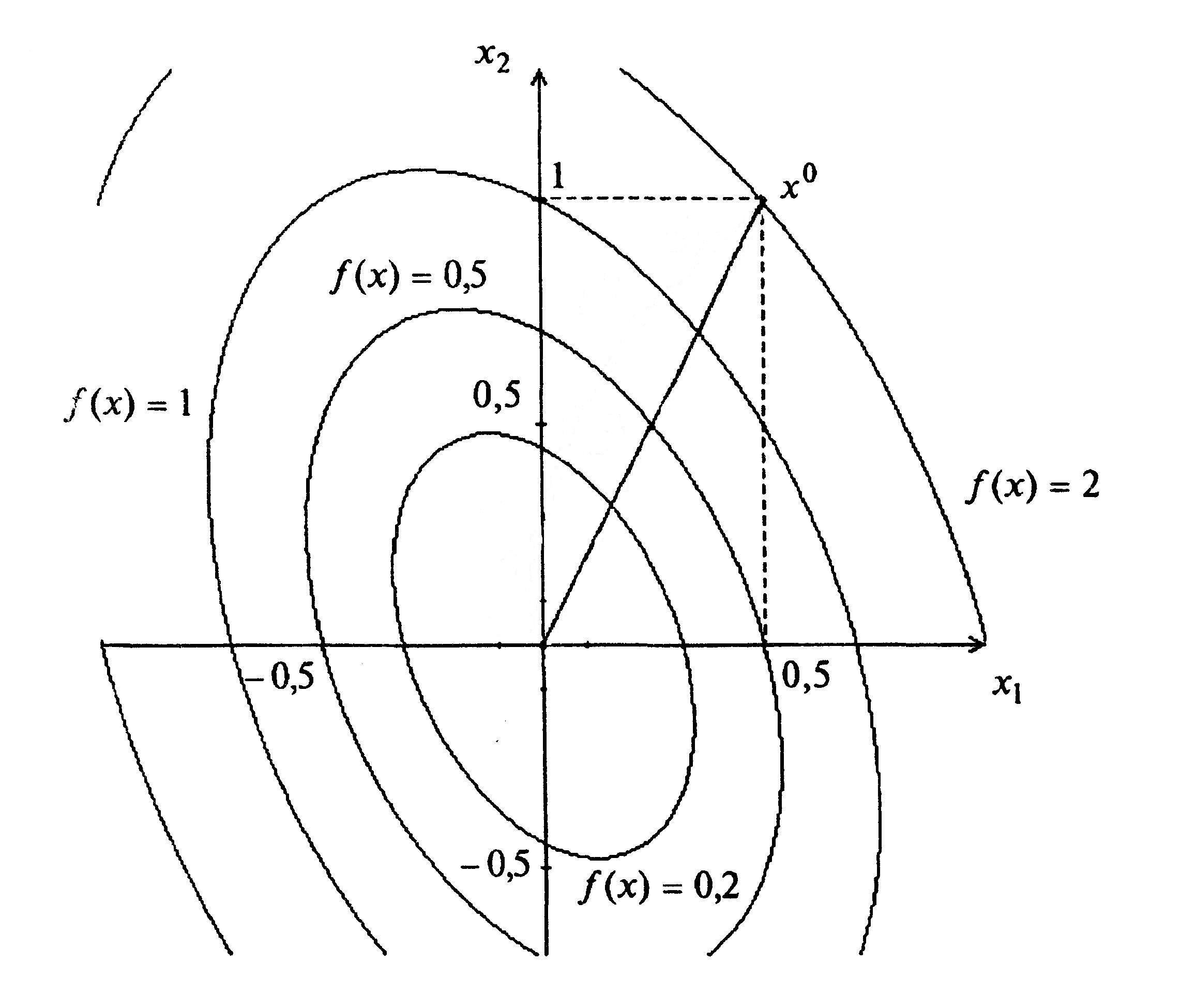
Рисунок 5.2.
