
- •Киров 2006
- •Рецензент: к.Т.Н., доцент каф. Эвм Матвеева л.И.
- •1 Оформление лабораторной работы
- •1.1 Цель работы
- •1.2 Формирование отчета
- •2 Общие принципы методов поиска безусловного экстремума
- •3 Методы нулевого порядка
- •3.1 Метод конфигураций (метод Хука - Дживса)
- •3.2 Метод деформируемого многогранника
- •3.3 Метод вращающихся координат (метод Розенброка)
- •3.4 Метод сопряженных направлений (метод Пауэлла)
- •4 Методы первого порядка
- •4.1 Метод градиентного спуска с постоянным шагом
- •4.2 Метод наискорейшего градиентного спуска (Метод Коши)
- •4.3 Метод Гаусса - Зейделя
- •4.4 Метод сопряженных градиентов (Флетчера – Ривса)
- •5 Методы второго порядка
- •5.1 Метод Ньютона
- •5.2 Метод Ньютона - Рафсона
- •5.3 Метод Марквардта
- •6 Пример отчета по лабораторной работе
- •7 Блок вариантов заданий
- •8 Библиографический список
3 Методы нулевого порядка
В этих методах для определения направления спуска не требуется вычислять производные целевой функции. Направление минимизации в данном случае полностью определяется последовательными вычислениями значений функции. Следует отметить, что при решении задач безусловной минимизации методы первого и второго порядков обладают, как правило, более высокой скоростью сходимости, чем методы нулевого порядка. Однако на практике вычисления первых и вторых производных функции большого количества переменных часто оказываются слишком трудоемкими либо их принципиально невозможно осуществить по причине отсутствия явных выражений не только для производных, но и для самой функции. Иногда самое большее, на что можно рассчитывать, это умение вычислять значение целевой функции задачи в заданной точке (например, так обстоит дело, если значение получается в результате эксперимента, параметры которого определяются аргументом целевой функции). В этом случае определение производных с помощью различных численных методов (аппроксимация производных по информации о значениях функции) осуществляется с ошибками, которые могут ограничить применение таких методов. Кроме того, на практике встречаются задачи, решение которых возможно лишь с помощью методов нулевого порядка, например задачи минимизации функций с разрывными первыми производными. Для решения многих практических задач оптимизации могут быть успешно применены методы нулевого порядка.
3.1 Метод конфигураций (метод Хука - Дживса)
Метод конфигураций (метод Хука-Дживса [R. Hook, T.A. Jeeves]) представляет собой комбинацию исследующего (пробного) поиска с циклическим изменением переменных и ускоряющего поиска по образцу. Исследующий поиск ориентирован на выявление локального поведения целевой функции и определение направления ее убывания вдоль "оврагов". Полученная информация используется при поиске по образцу при движении вдоль "оврагов".
Исследующий
поиск начинается в некоторой начальной
точке
![]() ,
называемой старым базисом. В качестве
множества направлений поиска выбирается
множество координатных направлений.
Задается величина шага, которая может
быть различной для разных координатных
направлений и переменной в процессе
поиска. Фиксируется первое координатное
направление и делается шаг в сторону
увеличения соответствующей переменной.
Если значение функции в пробной точке
меньше значения функции в исходной
точке, шаг считается удачным. В противном
случае необходимо вернуться в предыдущую
точку и сделать шаг в противоположном
направлении с последующей проверкой
поведения функции. После перебора всех
координат исследующий поиск завершается.
Полученная точка называется новым
базисом (на рис. 3.1 в точке
произведен исследующий поиск и получена
точка
,
называемой старым базисом. В качестве
множества направлений поиска выбирается
множество координатных направлений.
Задается величина шага, которая может
быть различной для разных координатных
направлений и переменной в процессе
поиска. Фиксируется первое координатное
направление и делается шаг в сторону
увеличения соответствующей переменной.
Если значение функции в пробной точке
меньше значения функции в исходной
точке, шаг считается удачным. В противном
случае необходимо вернуться в предыдущую
точку и сделать шаг в противоположном
направлении с последующей проверкой
поведения функции. После перебора всех
координат исследующий поиск завершается.
Полученная точка называется новым
базисом (на рис. 3.1 в точке
произведен исследующий поиск и получена
точка
![]() -
новый базис). Если исследующий поиск с
данной величиной шага неудачен, то
она уменьшается и процедура продолжается.
Поиск заканчивается, когда текущая
величина шага станет меньше некоторой
величины.
-
новый базис). Если исследующий поиск с
данной величиной шага неудачен, то
она уменьшается и процедура продолжается.
Поиск заканчивается, когда текущая
величина шага станет меньше некоторой
величины.
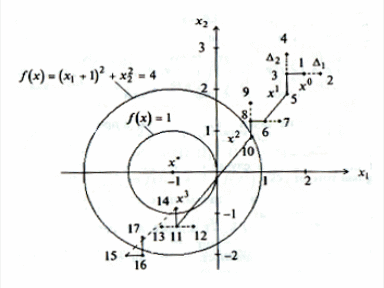
Рисунок 3.1
Поиск
по образцу заключается в движении по
направлению от старого базиса к новому
(от точки
через точку
,
из точки
через точку
![]() ,
из точки
через точку
,
из точки
через точку
![]() на рис. 3.1). Величина ускоряющего шага
задается ускоряющим множителем
на рис. 3.1). Величина ускоряющего шага
задается ускоряющим множителем
![]() .
Успех поиска по образцу определяется
с помощью исследующего поиска из
полученной точки (например, из точек 6,
11, 15 на рис. 3.1). Если при этом значение в
наилучшей точке меньше, чем в точке
предыдущего базиса, то поиск по образцу
удачен (точки 6, 11 - результат удачного
поиска по образцу, а точка 15 - неудачного).
Если поиск по образцу неудачен, происходит
возврат в новый базис, где продолжается
исследующий поиск с уменьшенным шагом.
.
Успех поиска по образцу определяется
с помощью исследующего поиска из
полученной точки (например, из точек 6,
11, 15 на рис. 3.1). Если при этом значение в
наилучшей точке меньше, чем в точке
предыдущего базиса, то поиск по образцу
удачен (точки 6, 11 - результат удачного
поиска по образцу, а точка 15 - неудачного).
Если поиск по образцу неудачен, происходит
возврат в новый базис, где продолжается
исследующий поиск с уменьшенным шагом.
На
рис. 3.1 удачный поиск отображается
сплошными линиями, а неудачный -
пунктирными, числа соответствуют
порождаемым алгоритмом точкам. Обозначим
через
![]() -
координатные направления
-
координатные направления
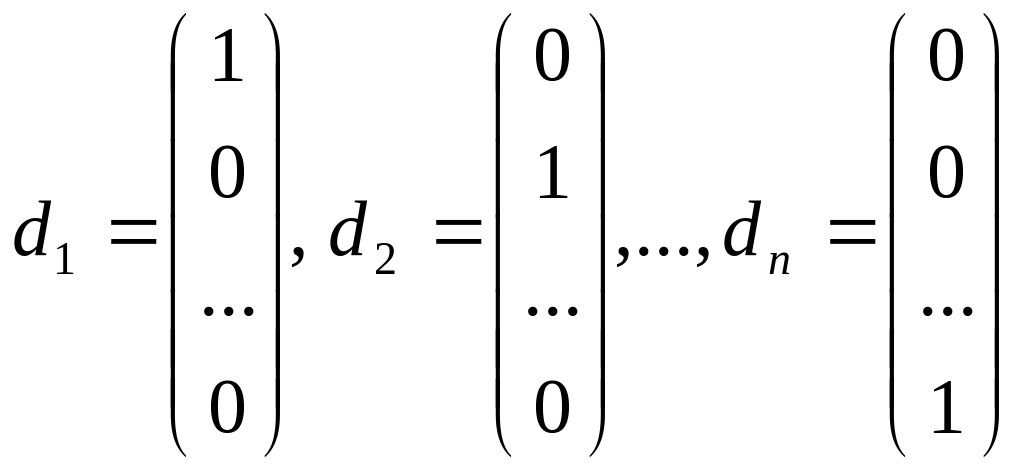
При
поиске по направлению
![]() меняется только переменная
меняется только переменная
![]() ,
а остальные переменные остаются
зафиксированными.
,
а остальные переменные остаются
зафиксированными.
Алгоритм:
Шаг
1. Задать
начальную точку
,
число
![]() для
остановки алгоритма, начальные величины
шагов по координатным направлениям
для
остановки алгоритма, начальные величины
шагов по координатным направлениям
![]() ,
ускоряющий множитель
,
ускоряющий множитель
![]() ,
коэффициент уменьшения шага
,
коэффициент уменьшения шага
![]() .
Положить
.
Положить
![]() .
.
Шаг 2. Осуществить исследующий поиск по выбранному координатному направлению:
если
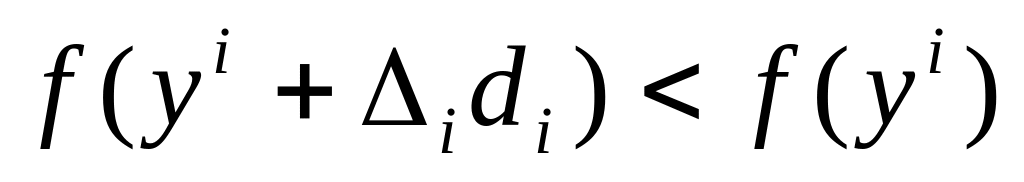 ,
шаг считается удачным. Положить
,
шаг считается удачным. Положить
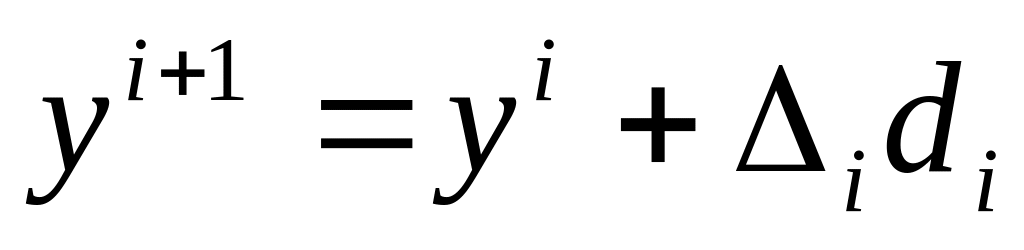 и перейти к шагу 3;
и перейти к шагу 3;если в пункте а) шаг неудачен, то делается шаг в противоположном направлении. Если
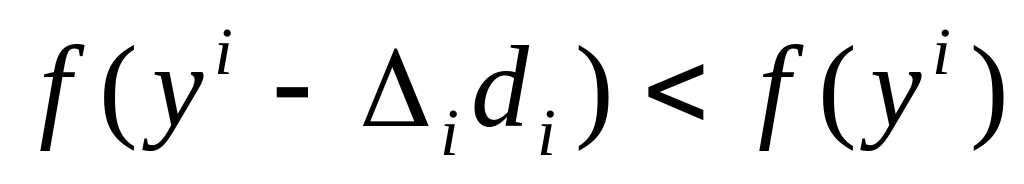 ,
шаг считается удачным. В этом случае
следует положить
,
шаг считается удачным. В этом случае
следует положить
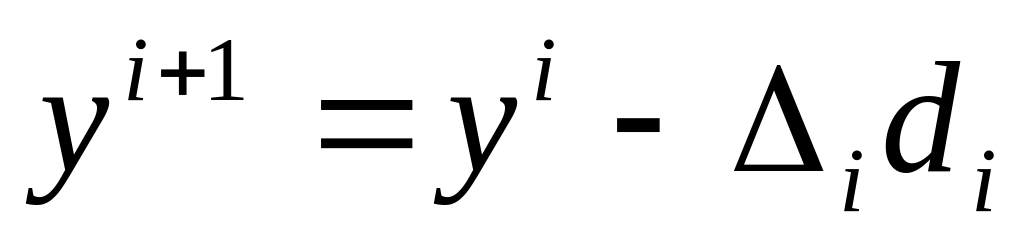 и перейти к шагу 3;
и перейти к шагу 3;если в пунктах а) и б) шаги неудачны, положить
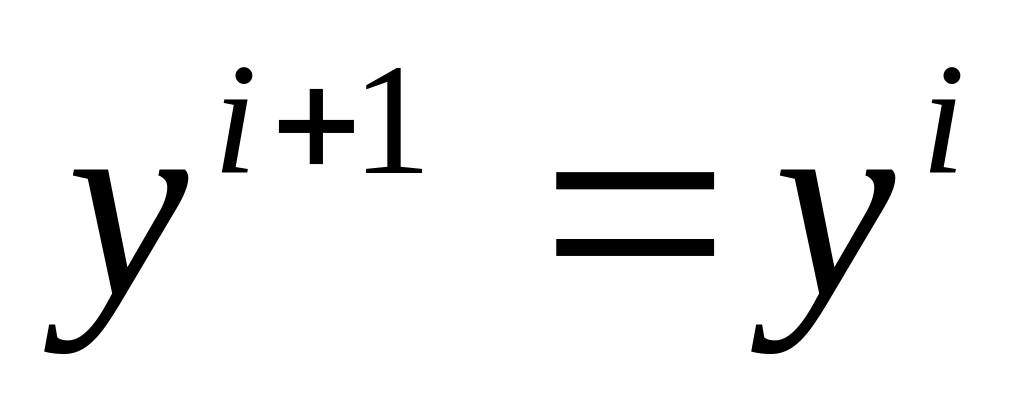 .
.
Шаг 3. Проверить условия:
если
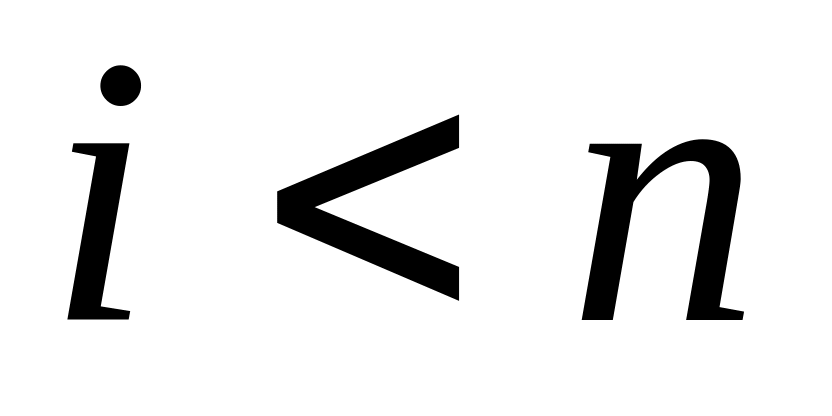 ,
то положить
,
то положить
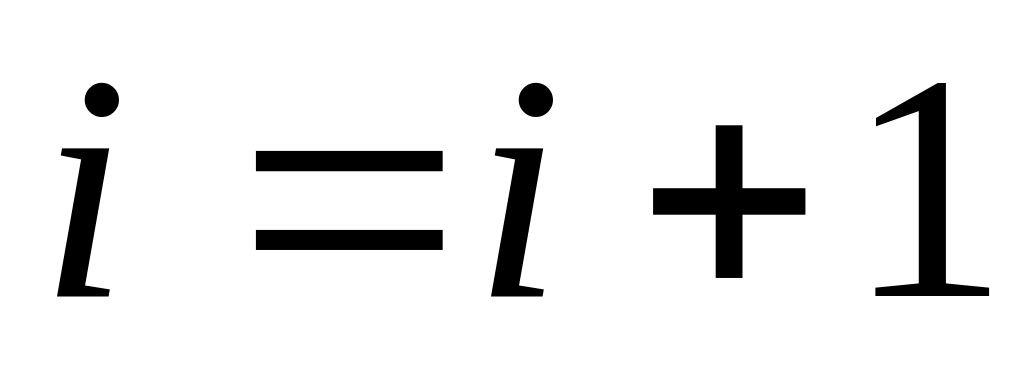 и перейти к шагу 2;
и перейти к шагу 2;если
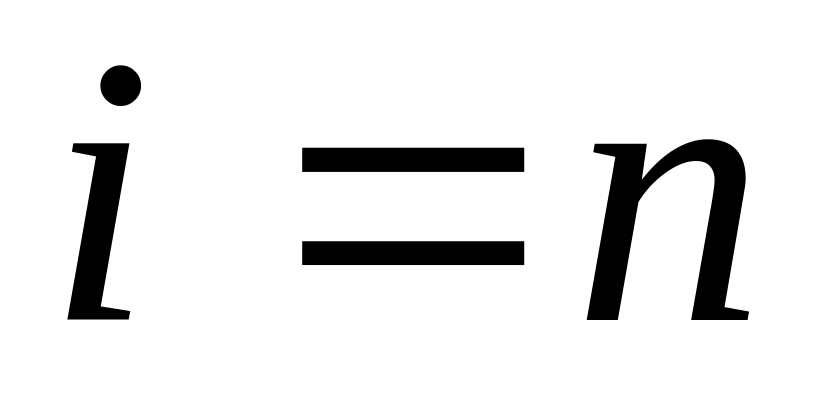 ,
проверить успешность исследующего
поиска
,
проверить успешность исследующего
поиска
-
если
![]() ,
перейти к шагу 4;
,
перейти к шагу 4;
-
если
![]() ,
перейти к шагу 5;
,
перейти к шагу 5;
Шаг
4. Провести
поиск по образцу. Положить
![]() ,
,
![]() ,
,
![]() ,
,
![]() и перейти к шагу 2.
и перейти к шагу 2.
Шаг 5. Проверить условие окончания:
если все
 ,
то поиск по закончить:
,
то поиск по закончить:
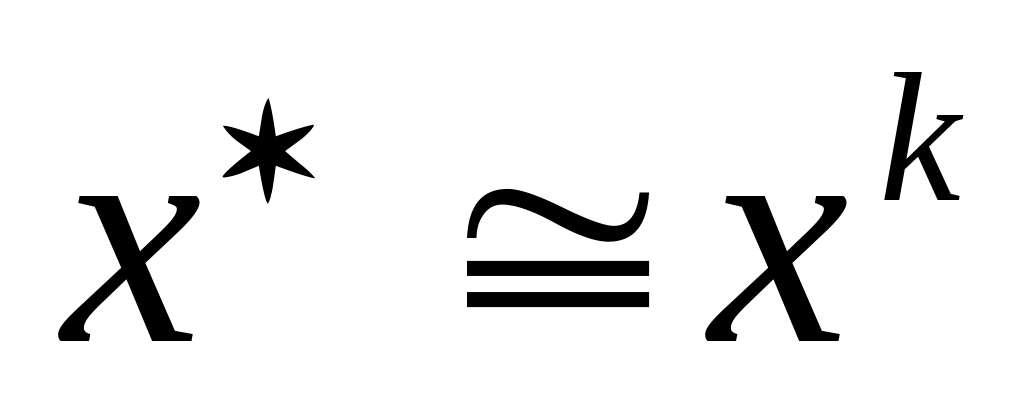 ;
;для тех
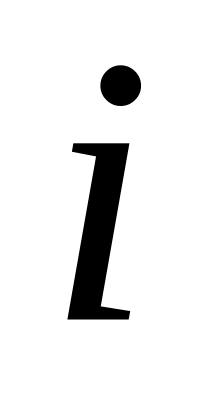 ,
для которых
,
для которых
 ,
уменьшить величину шага:
,
уменьшить величину шага:
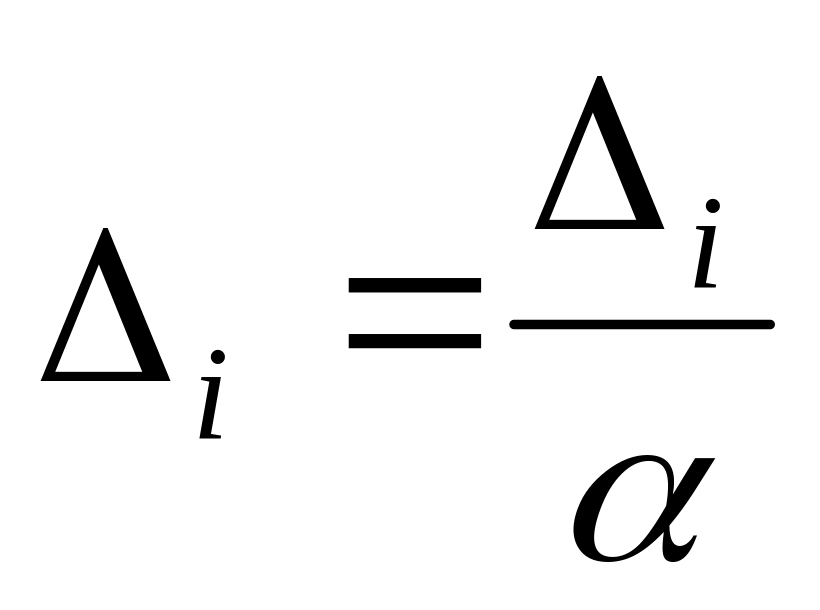 .
Положить
.
Положить
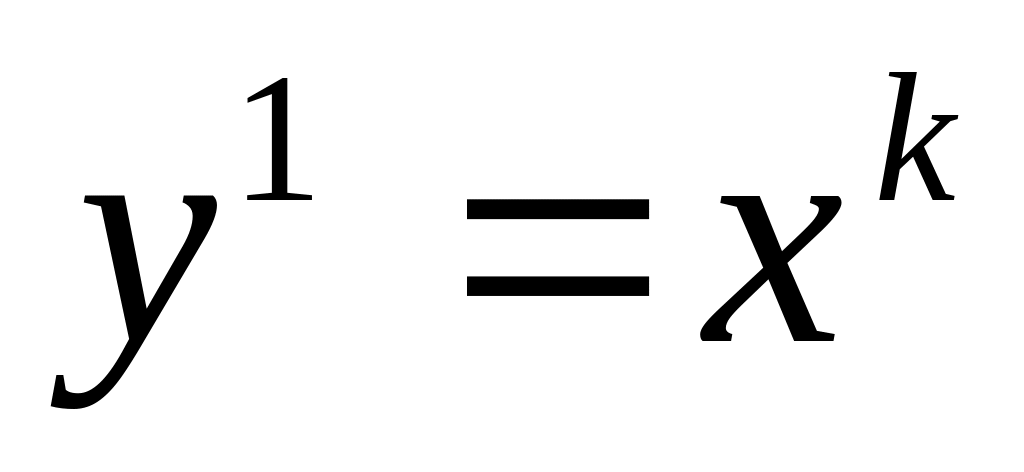 ,
,
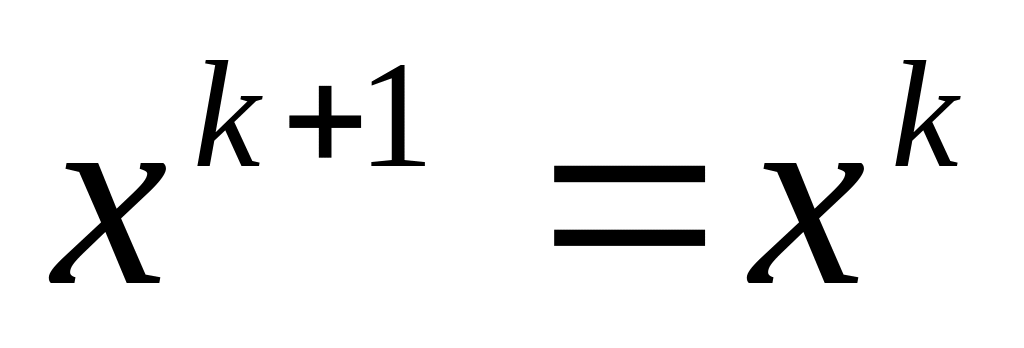 ,
,
и перейти к шагу 2
,
,
и перейти к шагу 2
Замечания:
а)
В алгоритме можно использовать одинаковую
величину шага по координатным направлениям,
то есть вместо
![]() применять
применять
![]() .
.
б) Существует модификация метода, где при исследующем поиске и поиске по образцу используется одномерная минимизация.
Пример: Найти локальный минимум функции методом конфигураций
![]()
Решение:
1.
Зададим
![]() - старый базис,
- старый базис,
![]()
![]() ,
,
![]() ,
,
![]() .
.
Положим
k
= 0, i
= 1,
![]() .
.
20.
Т.к.
![]() то шаг неудачен.
то шаг неудачен.
Т.к.
![]() то шаг удачный:
то шаг удачный:
![]() .
.
30. Т.к. i = 1 < 2 = n, то i = i + 1 = 2 и переходим к шагу 2.
21.
Т.к.
![]() то шаг неудачен.
то шаг неудачен.
Т.к.
![]() то шаг удачный:
то шаг удачный:
![]() .
.
31.
Т.к. i
= 2 = n
= 2 и
![]() ,
переходим к шагу 4.
,
переходим к шагу 4.
40.
Положим
![]() - новый базис, i
= 1, k
= k
+ 1 = 1, найдем
- новый базис, i
= 1, k
= k
+ 1 = 1, найдем
![]() .
Выполнен поиск по образцу. Переходим к
шагу 2.
.
Выполнен поиск по образцу. Переходим к
шагу 2.
22.
Т.к.
![]() и
и
![]() то
шаги неудачные, а
то
шаги неудачные, а
![]() .
.
32. Т.к. i = 1 < 2 = n, то i = i + 1 = 2 и переходим к шагу 2.
23.
Т.к.
![]() и
и
![]() то
шаги неудачные, а
то
шаги неудачные, а
![]() .
.
33.
Т.к. i
= 2 = n
= 2 и
![]() ,
переходим к шагу 4.
,
переходим к шагу 4.
41.
Положим
![]() - новый базис, i
= 1, k
= k
+ 1 = 2, найдем
- новый базис, i
= 1, k
= k
+ 1 = 2, найдем
![]() .
Выполнен поиск по образцу. Переходим к
шагу 2.
.
Выполнен поиск по образцу. Переходим к
шагу 2.
24.
Т.к.
![]() то шаг удачен:
то шаг удачен:
![]() .
.
34. Т.к. i = 1 < 2 = n, то i = i + 1 = 2 и переходим к шагу 2.
25.
Т.к.
![]() то шаг удачен:
то шаг удачен:
![]() .
.
35.
Т.к. i
= 2 = n
= 2 и
![]() ,
то поиск по образцу неудачен. Осуществляется
возврат в точку
,
то поиск по образцу неудачен. Осуществляется
возврат в точку
![]() .
Переходим к шагу 5.
.
Переходим к шагу 5.
50.
Т.к.
![]() то уменьшим шаг:
то уменьшим шаг:
![]() Положим
Положим
![]() i
= 1, k
= k
+ 1 = 3 и перейдем
к шагу 2.
i
= 1, k
= k
+ 1 = 3 и перейдем
к шагу 2.
26.
Т.к.
![]() и
и
![]() то
шаги неудачные, а
.
то
шаги неудачные, а
.
36. Т.к. i = 1 < 2 = n, то i = i + 1 = 2 и переходим к шагу 2.
27.
Т.к.
![]() и
и
![]() то
шаги неудачные, а
.
то
шаги неудачные, а
.
37.
Т.к. i
= 2 = n
= 2 и
![]() ,
то исследующий поиск неудачен. Перейдем
к шагу 5.
,
то исследующий поиск неудачен. Перейдем
к шагу 5.
51.
Т.к.
![]() то поиск закончен:
то поиск закончен:
![]() .
.
Геометрическая интерпретация решения задачи представлена на рисунке 3.2. Здесь изображены полученные точки; сплошной линией отмечены удачные итерации, а пунктирной – неудачные.
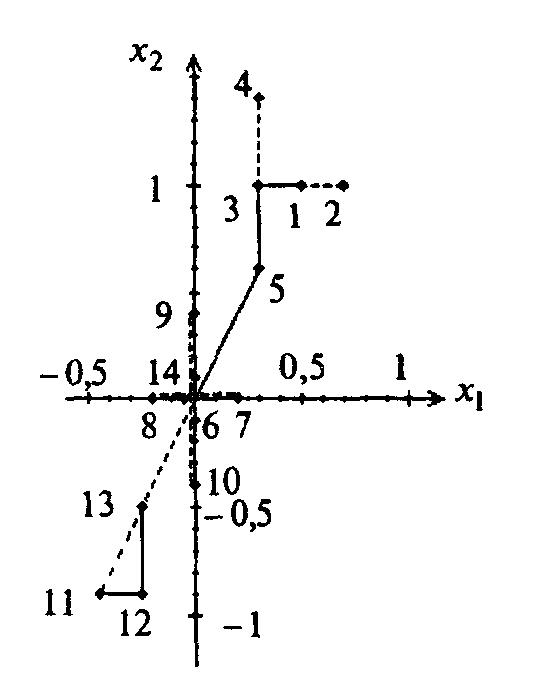
Рисунок 3.2
